TZOJ 3348: 线段相交Ⅲ（叉乘+快速排斥实验+跨立实验）

线段相交有两种情形：一种是“规范相交”，另一种是“非规范相交”。规范相交是指两条线段恰有唯一一个不是端点的公共点。即如果一条线段的端点在另一条线段上则不视为相交。如果两条线段有部分重合，也不视为相交。而非规范相交则把以上两种情况都视为相交。如下图所示：

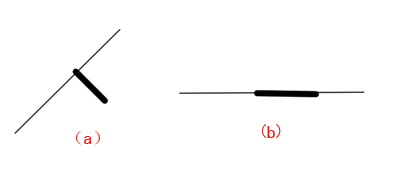
规范相交认为a，b两种情况都是不相交的，而非规范相交认为a，b两种情况都是相交的。

本题要求判断两条线段是否相交。如果是规范相交则输出YES，并输出交点坐标，如果是非规范相交则只需输出YES，如果不相交则输出NO。

输入

输入有多组数据，T表示输入数据的组数。每组测试数据有两行第一行输入一条线段的两个端点的坐标，第二行输入另一个线段的两个端点的坐标。

输出

对于每组测试数据，输出一行。如果是规范相交则输出YES，并输出交点坐标（小数点后面保留3位），如果是非规范相交则只需输出YES，如果不相交则输出NO。

样例输入

4
0 0 1 1
0 1 1 0
0 0 2 2
2 2 3 3
0 0 2 2
1.5 1.5 3 3
0 0 1 1
2 2 3 3

样例输出

YES (0.500,0.500)
YES
YES
NO

题目来源

TZOJ

思路：判断线段相交用叉乘+快速排斥

第一步：快速排斥实验

如果两线段在x，y的投影都不重合，是不可能会相交的。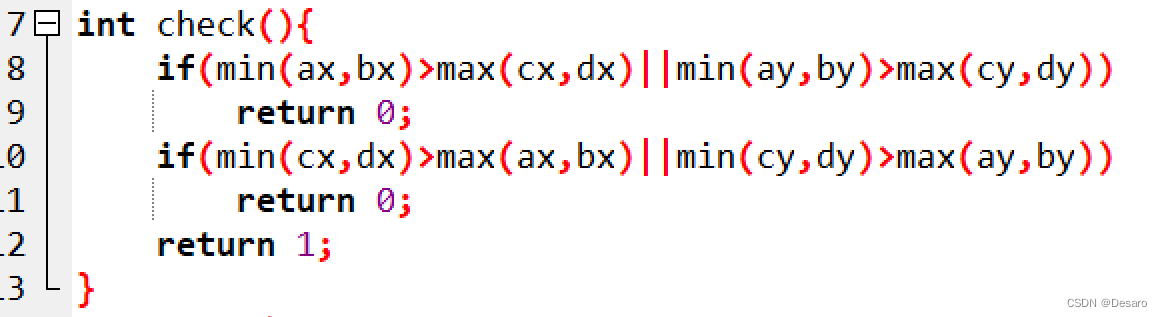

第二步：跨立实验 

两个坐标A(x1,y1),B(x2,y2),那么AxB的向量积就是x1y2-y1x2。
我们假定一个向量积R，R=x1y2-y1x2。
R<0 说明A在B的逆时针方向
R=0 说明A与B共线，可能正向也可能反向
R>0 说明A在B的顺时针方向

判断要两组，以A为顶点的三条向量 + 以C为顶点的三条向量

若此时A线段向量在L1，L2的中间或L1，L2的边上，就能说明B跨立A
即L1，L2在A的不同的顺逆时针方向，就可以分别求出两个L的向量积，再将他们相乘，如果结果<=0,即向量积异号或有0。

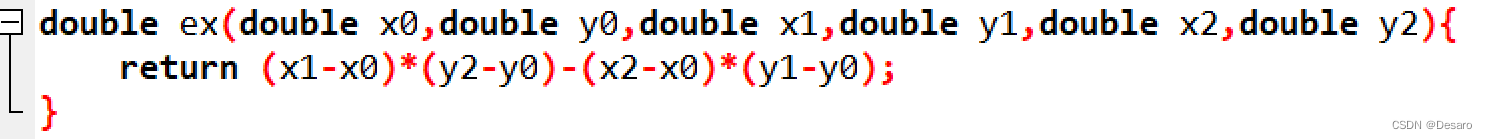
判断规范相交

 判断不规范相交

最后就是用二次函数y=kx+b或者先前有的向量叉乘直接求点坐标

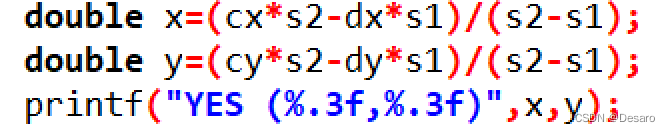
 下午做得人都要傻掉了也没做出来，痛、太痛了

AC的代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=30;
const double eps=1e-6;
double ax,ay,cx,cy,dx,dy,bx,by;
int check(){
    if(min(ax,bx)>max(cx,dx)||min(ay,by)>max(cy,dy))
        return 0;
    if(min(cx,dx)>max(ax,bx)||min(cy,dy)>max(ay,by))
        return 0;
    return 1;
}
double ex(double x0,double y0,double x1,double y1,double x2,double y2){
    return (x1-x0)*(y2-y0)-(x2-x0)*(y1-y0);
}
int judge(double x){
    if(fabs(x)<eps)
        return 0;
    return x>0? 1:-1;
}
void find(){
    double a1=dy-cy,a2=cy-ay,a3=by-ay;
    double b1=dx-cx,b2=cx-ax,b3=bx-ax;
    double t=(a3*b2-a2*b3)/(a1*b3-a3*b1);
    double y=a1*t+cy;
    double x=b1*t-cx;
    printf(" (%.3f,%.3f)",x,y);
    return;
}
void solve(){
    //(A-C) x (D-C) * (B-C) x (D-C) < 0
    //C D 在向量ab的两侧 
    //(C-A) x (B-A) * (D-A) x (B-A) < 0
    double s1=ex(ax,ay,bx,by,cx,cy);
    double s2=ex(ax,ay,bx,by,dx,dy);
    double s3=ex(cx,cy,dx,dy,ax,ay);
    double s4=ex(cx,cy,dx,dy,bx,by);
    int d1=judge(s1),d2=judge(s2),d3=judge(s3),d4=judge(s4);
    //判断规范相交
    if((d1*d2<0)&&(d3*d4<0)){
        //find(); //交点坐标 
        double x=(cx*s2-dx*s1)/(s2-s1);
        double y=(cy*s2-dy*s1)/(s2-s1);
        printf("YES (%.3f,%.3f)",x,y); 
        return;
    }
    //判断非规范相交
    //d1==0, 则证明a,b,c三点共线; 
    s1=ex(cx,cy,ax,ay,bx,by);
    s2=ex(dx,dy,ax,ay,bx,by);
    s3=ex(ax,ay,cx,cy,dx,dy);
    s4=ex(bx,by,cx,cy,dx,dy);
    int k1=judge(s1),k2=judge(s2),k3=judge(s3),k4=judge(s4);
    if(d1==0&&k1<=0||d2==0&&k2<=0||d3==0&&k3<=0||d4==0&&k4<=0){
        cout<<"YES";
        return;
    }
    cout<<"NO";
    return;
}
int main()
{
    int t;
    cin>>t;
    while(t--){
        cin>>ax>>ay>>bx>>by;
        cin>>cx>>cy>>dx>>dy;
        if(!check()){
            cout<<"NO";
            if(t) cout<<endl;
            continue;
        }
        solve();
        if(t) cout<<endl;
    }
    return 0;
}