zoj 1648 Circuit Board（跨立相交实验 线段与线段）

题目链接：zoj 1648

题意：给出n条边，问：如果有相交，输出burned！，没有输出ok！，注意下，这题还说了，相交于端点是不算交叉的。

参考链接：http://dev.gameres.com/Program/Abstract/Geometry.htm

https://blog.csdn.net/freezhanacmore/article/details/7894751

http://www.cnblogs.com/TangMoon/archive/2017/09/29/7611115.html

判断两线段是否相交：

　我们分两步确定两条线段是否相交：

　(1)快速排斥试验

　　　设以线段 P1P2 为对角线的矩形为R， 设以线段 Q1Q2 为对角线的矩形为T，如果R和T不相交，显然两线段不会相交。

P1坐标为（p1x,p1y）,P2坐标为（p2x,p2y），Q1的坐标为（q1x,q1y），Q2的坐标为（q2x,q2y)。

那矩形相交的条件就是：

min(p1x,p2x) <= max(q1x,q2x) &&
min(q1x,q2x) <= max(p1x,p2x) &&
min(p1y,p2y) <= max(q1y,q2y) &&
min(q1y,q2y) <= max(p1y,p2y);

　(2)跨立试验

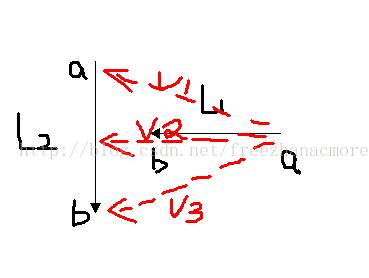
　　　　如果两线段相交，则两线段必然相互跨立对方。若P1P2跨立Q1Q2 ，则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。上式可改写成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上。所以判断P1P2跨立Q1Q2的依据是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。同理判断Q1Q2跨立P1P2的依据是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0。具体情况如下图所示：

在相同的原理下，对此算法的具体的实现细节可能会与此有所不同，除了这种过程外，大家也可以参考《算法导论》上的实现。

　判断线段和直线是否相交：

　有了上面的基础，这个算法就很容易了。如果线段P1P2和直线Q1Q2相交，则P1P2跨立Q1Q2，即：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。（这里等于0，表示的是相交于端点，注意看清题意）

注意：一般情况下，为了避免跨立不相交的局面，一定要判断线段P1P2跨立Q1Q2后再反过来判断Q1Q2跨立P1P2如果两者都跨立，才能断定他们相交

///P1P2 横跨 Q1Q2：/// ( P1 - Q1 )×( Q2 - Q1 )*( Q2 - Q1 )×( P2 - Q1 ) > =0#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>const int maxn=2010;int min(int a,int b){return a>b?b:a;
}
int max(int a,int b){return a>b?a:b;
}struct point
{double x,y;point() {}point(double _x,double _y){x=_x;y=_y;}point operator -(const point &b) const{return point(x-b.x,y-b.y);}
};struct Line
{point a,b;Line() {}Line(point _a,point _b){a=point(_a.x,_a.y);b=point(_b.x,_b.y);}
}line[maxn];double Cross(point a,point b) ///叉积
{
//    printf("a.x=%f,a.y=%f,b.x=%f,b.y=%f\n",a.x,a.y,b.x,b.y);return a.x*b.y-a.y*b.x;
}const double esp=1e-5;int dcmp(double x)
{if(fabs(x)<esp) return 0;else return x>0?1:-1;
}
bool isCross(Line L1,Line L2) ///判断跨立相交
{///第一步 快速排斥实验if(!(min(L1.a.x,L1.b.x)<=max(L2.a.x,L2.b.x)&&min(L2.a.x,L2.b.x)<=max(L1.a.x,L1.b.x)&&min(L1.a.y,L1.b.y)<=max(L2.a.y,L2.a.y)&&min(L2.a.y,L2.b.y)<=max(L1.a.y,L1.b.y))) return false;///L2横跨L1double tmp1=Cross(L2.a-L1.a,L1.b-L1.a);double tmp2=Cross(L1.b-L1.a,L2.b-L1.a);///L1横跨L2double tmp3=Cross(L1.a-L2.a,L2.b-L2.a);double tmp4=Cross(L2.b-L2.a,L1.b-L2.a);//    printf("%f %f %f %f\n",tmp1,tmp2,tmp3,tmp4);if(dcmp(tmp1*tmp2)>0 && dcmp(tmp3*tmp4)>0) return true;///都大于0，就说明两线段相交，这里就不等于0了，因为题目已经要求了不算入端点相交return false;
}
int main()
{int n;while(~scanf("%d",&n)){point a,b;for(int i=0;i<n;i++){scanf("%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y);line[i]=Line(a,b);}int flag=1;for(int i=1;i<n;i++) ///这里为什么不用双重循环？因为第3条边和第1条边只需比较一次就行了{for(int j=0;j<i;j++){if(isCross(line[i],line[j])){flag=0;break;}}}if(flag) printf("ok!\n");else printf("burned!\n");}return 0;
}