快速排斥实验amp;跨立实验判断两直线是否相交

本文主要是介绍快速排斥实验amp;跨立实验判断两直线是否相交，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

两条线段有且仅有一个公共点，且这个点不是任何一条线段的端点时，称这两条线段是严格相交的。

也就是说线段不严格相交时可以将端点作为交点，但本文不讨论不严格相交，只讨论严格相交的情况（即使它们在算法实现上差别不大）。

在判断两条线段是否相交时，我们常用快速排斥实验跟跨立实验这两种方法，快速排斥实验能很快的排除掉线段不相交的情况，但并没法成为线段相交的充要条件，在快速排斥实验之后接上跨立实验就能完全的判断两线段是否相交，但其实只用跨立实验这一种办法也能作为判断线段相交的充要条件。

1.快速排斥实验：

假设以线段P1，P2为对角线作一矩形R，再以Q1,Q2为对角线作矩形T，当两个矩形不相交的时候两条线段肯定不相交，即线段相交的必要条件时矩形相交。

2.跨立实验：

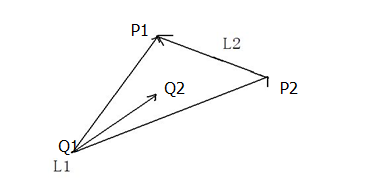
若P1P2跨立Q1Q2，即 向量Q1P1和向量Q1P2分布向量Q1Q2的两侧，满足(P1−Q1)×(Q2−Q1)∗(P2−Q1)×(Q2−Q1)<0。
若(P1−Q1)×(Q2−Q1)∗(P2−Q1)×(Q2−Q1)=0，说明P1或P2在直线Q1Q2上，但因为已通过快速排斥试验，所以这两线段是相交的。
故上式可改写成 (P1−Q1)×(Q2−Q1)∗(P2−Q1)×(Q2−Q1)≤0
同理，若Q1Q2跨立P1P2，则要满足(Q1−P1)×(P2−P1)∗(Q2−P1)×(P2−P1)≤0
当P1P2跨立Q1Q2且Q1Q2跨立P1P2，跨立试验成功。

struct point{double x,y;
}P1,P2,Q1,Q2;
struct Edge
{point a,b;
}e[N];
double xmult(point a,point b,point c) //大于零代表a,b,c左转
{return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
bool OnSegment(point a,point b,point c)         //a,b,c共线时有效
{return c.x>=min(a.x,b.x)&&c.x<=max(a.x,b.x)&&c.y>=min(a.y,b.y)&&c.y<=max(a.y,b.y);
}bool Cross(point a,point b,point c,point d) //判断ab 与cd是否相交
{double d1,d2,d3,d4;d1=xmult(c,d,a);d2=xmult(c,d,b);d3=xmult(a,b,c);d4=xmult(a,b,d);if(d1*d2<0&&d3*d4<0)  return 1;else    if(d1==0&&OnSegment(c,d,a)) return 1;else    if(d2==0&&OnSegment(c,d,b)) return 1;else    if(d3==0&&OnSegment(a,b,c)) return 1;else    if(d4==0&&OnSegment(a,b,d)) return 1;return 0;
}

这篇关于快速排斥实验amp;跨立实验判断两直线是否相交的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！