贝塞尔专题
nurbs曲面和贝塞尔曲面的区别是什么
NURBS曲面和贝塞尔曲面的主要区别如下: 定义与理论基础: NURBS曲面:全称非均匀有理B样条曲面,是NURBS曲线在二维空间上的扩展。它结合了非均匀性、有理性和B样条的特性,能够更灵活地表示复杂曲面。 贝塞尔曲面:通过Bernstein基函数的张量积为加权系数对控制顶点进行线性组合所构造的参数曲面。它具有良好的连续性和插值性质。 控制点的灵活性与局部性: N
自定义控件(31)---贝塞尔曲线
布局文件 <com.safly.myapplication.CustomeWaitingProgressBar2android:id="@+id/skipView2"android:layout_width="fill_parent"android:layout_height="fill_parent"></com.safly.myapplication.CustomeWaitingPr
OpenGL 实践之贝塞尔曲线绘制
以下文章来源于微信公众号“音视频开发进阶” ,作者glumes 说到贝塞尔曲线,大家肯定都不陌生,网上有很多关于介绍和理解贝塞尔曲线的优秀文章和动态图。 以下两个是比较经典的动图了。 二阶贝塞尔曲线: 三阶贝塞尔曲线: 由于在工作中经常要和贝塞尔曲线打交道,所以简单说一下自己的理解: 现在假设我们要在坐标系中绘制一条直线,直线的方程很简单,就是 y=x ,很容易得到下图: 现在我们
Android 绘图贝塞尔曲线简单使用
Android 绘图贝塞尔曲线简单使用 在Android中某些自定义View的时候需要绘制某些曲线,这时候贝塞尔曲线就登场了。 我们不用深入了解贝塞尔曲线的详细信息,我们的最终目的还是需要学会如何使用。贝塞尔曲线分为3种,分别为一阶贝塞尔曲线、二阶贝塞尔曲线、三阶贝塞尔曲线。 一阶贝塞尔曲线 一阶贝塞尔曲线是一条直线,只需要指定两个点就可以画出了,简单粗暴的使用就是: canvas.d
Android自定义系列——8.Path之贝塞尔曲线
贝塞尔曲线能干什么 贝塞尔曲线作用十分广泛,简单举几个的栗子: QQ小红点拖拽效果一些炫酷的下拉刷新控件阅读软件的翻书效果一些平滑的折线图的制作很多炫酷的动画效果 理解贝塞尔曲线的原理 一阶曲线原理: 一阶曲线是没有控制点的,仅有两个数据点(A 和 B),最终动态过程如下: (本文中贝塞尔曲线相关的动态演示图片来自维基百科)。一阶曲线其实就是前面讲解过的lineTo。 二阶曲线
PullBezierZoomView 一个具有贝塞尔曲线下拉效果的自定义view
该控件效果基于PullZoomView源码改动的而来,感谢Frank-Zhu的开源代码.该控件具有下拉放大背景图和贝塞尔曲线的效果. github:https://github.com/X-FAN/PullBezierZoomView 欢迎star 我主要写了一个自定义的贝塞尔曲线的效果的控件并整合到了Frank-Zhu的项目中的一个子项中. 这里面有个小数学知识的求解,因为效果要贝赛尔曲线
canvas效果案例:贝塞尔曲线
绘制二次贝塞尔曲线 ctx.quadraticCurveTo(x1, y1, x, y);从上一点开始绘制一条二次曲线,到(x, y)为止,并且以(x1, y1)作为控制点ctx.beginPath();ctx.strokeStyle = 'green';ctx.lineWidth = 4;// 起始点ctx.moveTo(100, 400);//(从上一点)ctx.quadrati
【Spine学习11】之 战士攻击动作 思路总结(手动调整贝塞尔曲线实现前快后慢)
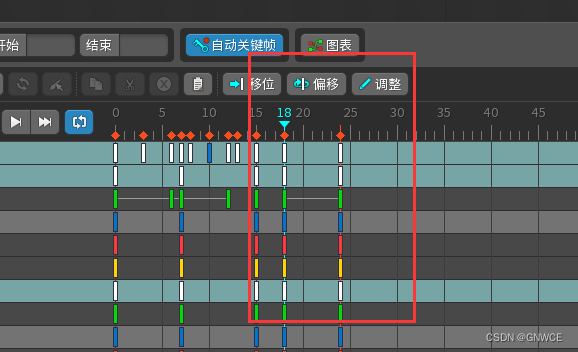
拿到一份psd文件先观察检查一下图片顺序有没有问题, 重点看一下人物的腿部分层,(如果是大小腿分开画的就网格可打可不打,如果是连在一起画的,那必须打网格) 拿着剑的时候剑和手的层级有没有错位, 有错位调整好一下位置: 筛选-插槽-拖拽这个插槽:更改图片顺序 攻击动作组成部分: 第一步: 导入文件 打开PSD文件-用脚本输出json文件和images文件夹 打开spine 导入数据 选择对应j
关于photoshop钢笔工具中各点对应到“贝塞尔曲线”中的含义(cocos2d-x与iOS)
1.程序中贝塞尔曲线的简单介绍,只介绍曲线部分。 程序中的贝塞尔曲线需要四个点:起始点(startPoint) ,控制点1(controlPoint1),控制点2( controlPoint2),结束点(endPoint)。 起始点和结束点确定曲线端点,两个控制点确定曲线形状。 一般sdk中关于贝塞尔曲线api的参数一般有三个:控制点1( controlPoint1),控制点2( c
Qt 中实现任意阶贝塞尔曲线绘制 动态调节
【写在前面】 Qt 中有相当方便的绘制接口 ( 由 QPainter 提供 ) 。 例如贝塞尔曲线的 API: QPainterPath 的 quadTo() 和 cubicTo() 然后使用 QPainter::drawPath()。 然而,美中不足的是,Qt 的贝塞尔曲线只支持二次和三次,对于更高阶的似乎就无能为力了。
Android之可伸缩的皮筋效果(贝塞尔曲线)的介绍
贝塞尔曲线 引言: 为什么我要写这篇关于贝塞尔曲线的博客,在android里面很多地方都用到了,比如当我们看到一个效果像橡皮筋拉伸一样,有弹性,一般就会用到贝赛尔曲线,不知道细心的你有没有发现,比如,我们看到QQ里面有那个红色的气泡的可以按着拖动,还有一些引导页里面几个点,我们滑动页面的时候,下面的几个点就想被挤压了,然后有一种被拖动的效果,还有就是我们做翻页的效果的时候要也会
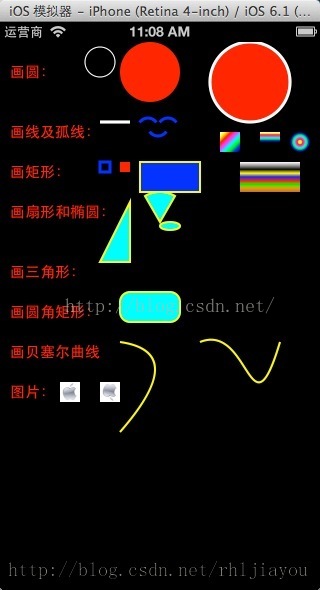
Quartz 2d 用CGContextRef 绘制各种图形 (文字、圆、直线、弧线、矩形、扇形、椭圆、三角形、圆角形、贝塞尔曲线、图片)
首先了解下 CGContextRef Graphics Context是图形上下文,可以将其理解为一块画布,我们可以在上面进行绘画操作,绘制完成后,将画布放到我们的View 中显示即可,View看着是一个画框。 自己学习时实现的Demo,希望对大家有帮助,具体的实现看代码,并有完美的注释解释,还有一些对我们帮助的博文供大家参考。 看下Demo 效果图先: 自定义Cu
Android 利用属性动画结合贝塞尔曲线方程编写好看的动画.
研究一下贝塞尔曲线. /*** 贝塞尔方程*/private class BeizerEvaluator implements TypeEvaluator<PointF> {private PointF point1;private PointF point2;private PointF pointF;public BeizerEvaluator(PointF point1, Poin
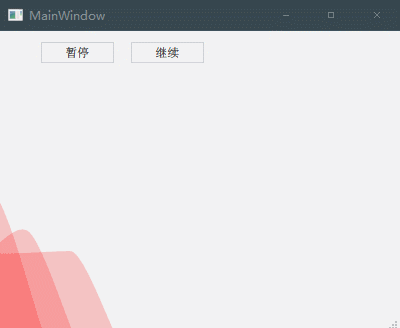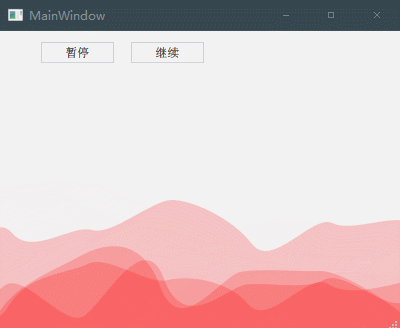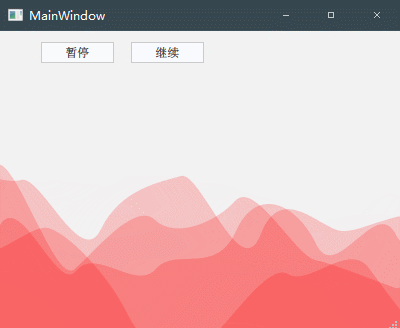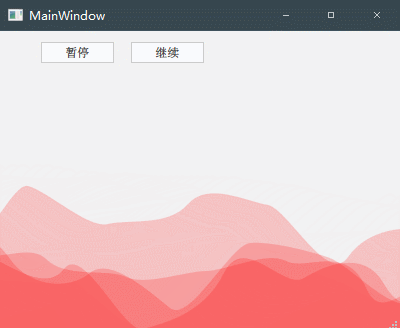
《QT实用小工具·六十二》基于QT实现贝塞尔曲线画炫酷的波浪动画
1、概述 源码放在文章末尾 该项目实现了通过贝塞尔曲线画波浪动画,可控制 颜色+密度+速度+加速度 安装与运行环境 语言:C++ 框架:Qt 11.3 平台:Windows 将屏幕水平平均分为10块,在一定范围内随机高度的12个点(左右出头),通过贝塞尔曲线连接连续的点,即可绘制成一段段连续的波浪。 但是每两端波浪都会有折线凸起,根据贝塞尔曲线的原理,两个控制点中点作为新的控制点,原来的两点
贝塞尔曲线 java
参考文章: 理解贝塞尔曲线https://blog.csdn.net/weixin_42301220/article/details/125167672 代码实现参考 https://blog.csdn.net/yinhun2012/article/details/118653732 贝塞尔 一二三阶java代码实现,N阶段可以通过降阶递归实现 public class Test ext
UIBezierPath贝塞尔弧线常用方法记
/根据一个矩形画曲线 (UIBezierPath *)bezierPathWithRect:(CGRect)rect //根据矩形框的内切圆画曲线 (UIBezierPath *)bezierPathWithOvalInRect:(CGRect)rect //根据矩形画带圆角的曲线 (UIBezierPath *)bezierPathWithRoundedRect:(CGRect)rec
探索CSS中的贝塞尔曲线cubic-bezier()函数:掌握自定义动画曲线的艺术
在CSS动画的世界里,平滑而自然的过渡效果是提升用户体验的关键。传统的线性或简单缓动效果有时无法满足复杂动画的需求,这时cubic-bezier()函数便大放异彩,它赋予开发者无限创意,让动画曲线随心所欲地定制。本文将深入解析cubic-bezier()的工作原理、使用方法、以及如何通过代码示例来实现那些令人惊艳的动画效果。 什么是cubic-bezier()函数? cubic-bezier(
Android中贝塞尔曲线的使用
Android中主要在onDraw方法中使用quadTo & cubicTo 画二次和三次贝塞尔曲线; 绘制贝塞尔曲线一般会结合moveTo一起使用, path.reset();path.moveTo(start.x,start.y);path.quadTo(control.x,control.y,end.x,end.y);canvas.drawPath(path, mPaint);/
一种简单的贝塞尔插值算法
转载地址:http://www.antigrain.com/research/bezier_interpolation/index.html#PAGE_BEZIER_INTERPOLATION Interpolation with Bezier CurvesA very simple method of smoothing polygons Initially, there was a q
【cocos creator】【TS】贝塞尔曲线,地图之间显示曲线,顺着曲线移动
参考: https://blog.csdn.net/Ctrls_/article/details/108731313 https://blog.csdn.net/qq_28299311/article/details/104009804 const { ccclass, property } = cc._decorator;@ccclassexport default class
Godot插值、贝塞尔曲线和Astar寻路
一、插值 线性插值是采用一次多项式上进行的插值计算,任意给定两个值A和B,那么在A和B之间的任意值可以定义为:P(t) = A * (1 - t) + B * t,0 <= t <= 1。 数学中用于线性拟合,游戏应用可以做出跟随效果(宠物跟随、npc跟随) const FOLLOW_SPEED = 4.0func _physics_process(delta):var mouse_pos =
unity 贝塞尔曲线实例化应用
项目中常常会用到画曲线的功能,不管是Gizmos.DarwLine还是Debug.DarwLine都满足不了打包之后在exe中显示。 虽然Linerenderer可以画,但是自己一点点的填写坐标非常麻烦。所以这里将用到贝塞尔曲线公式计算生成一条曲线以及生成一条曲线在Linerenderer中所需要多少个点位。 这里有篇博客将贝塞尔曲线的原理和推导公式都讲解的非常清楚,有兴趣可以了解下:http
windows程序设计(7):绘制贝塞尔曲线
#include <windows.h>#include <math.h>#define NUM 1000#define TWOPI (2*3.14159)LRESULT CALLBACK WndProc (HWND,UINT,WPARAM,LPARAM);int WINAPI WinMain(HINSTANCE hInstance, //当前实例句柄HINSTANCE hPrevI
无偏估计中贝塞尔系数的由来
对于采样自 X X X的独立同分布样本 x i : i ∈ [ 1 , n ] x_i: i\in[1,n] xi:i∈[1,n],用样本方差 s 2 s^2 s2去估计 X X X的方差 σ 2 \sigma^2 σ2,为什么要除以 n − 1 n-1 n−1而不是 n n n? 证明用 n n n除得到的估计 σ ^ 2 = σ 2 − E [ ( X ˉ − μ ) 2 ] \hat\s
unity3D中贝塞尔曲线的控制点计算
一、贝塞尔曲线的概念 对于两点之间的连线,我们可以用直线进行连接效果如下: 其中的每一个F点都在AB连接的线段上 这就是一阶贝塞尔曲线 如果我们加入一个控制点C,那么做图如下: 1、连接AC,BC 2、在AC,BC上找到 AD/AC = CE/CB 的点D,E