本文主要是介绍unity 贝塞尔曲线实例化应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
项目中常常会用到画曲线的功能,不管是Gizmos.DarwLine还是Debug.DarwLine都满足不了打包之后在exe中显示。
虽然Linerenderer可以画,但是自己一点点的填写坐标非常麻烦。所以这里将用到贝塞尔曲线公式计算生成一条曲线以及生成一条曲线在Linerenderer中所需要多少个点位。
这里有篇博客将贝塞尔曲线的原理和推导公式都讲解的非常清楚,有兴趣可以了解下:https://blog.csdn.net/cfan927/article/details/104649623/
我这里将用二次贝塞尔曲线公式在LineRenderer中画一条曲线,下面是原理图:
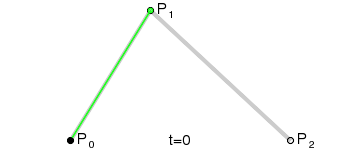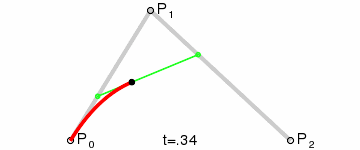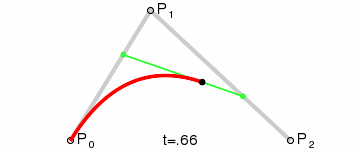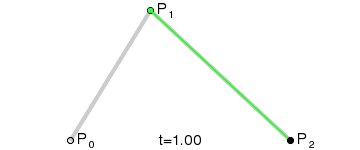
定义:二次贝塞尔曲线的路径由给定点P0 、P1、P2的函数B(t)给出:
B ( t ) = ( 1 − t ) 2 P 0 + 2 t ( 1 − t ) P 1 + t 2 P 2 , t ∈ [ 0 , 1 ]
我们在将该公式带入到unity中,将B理解为一个求导结果即Vector3向量,t为时间(即当前点移动到下一个点时间)t 取值0 - 1;
上代码:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class LineRender : MonoBehaviour
{private LineRenderer lineRenderer;public Vector3 p0;public Vector3 p1;public Vector3 p2;private Vector3 result;private List<Vector3> vectorList= new List<Vector3>();private float Nowtime = 0;private float timeLerp;private float maxTime = 1f;void Start(){lineRenderer = gameObject.GetComponent<LineRenderer>();p0 = new Vector3(0,0,0);p1 = new Vector3(5,5,5);p2 = new Vector3(10,0,10);}void FixedUpdate(){if (Nowtime > maxTime){return;}CalculateVectorPoint();lineRenderer.positionCount = vectorList.ToArray().Length;if (lineRenderer.positionCount >= 2){lineRenderer.SetPositions(vectorList.ToArray());}}void CalculateVectorPoint(){result = new Vector3();timeLerp = Mathf.Lerp(0, 1, Nowtime / maxTime);result.x = Mathf.Pow(1 - timeLerp, 2) * p0.x + 2 * timeLerp * Mathf.Pow(1 - timeLerp, 1) * p1.x + Mathf.Pow(timeLerp, 2) * p2.x;result.y = Mathf.Pow(1 - timeLerp, 2) * p0.y + 2 * timeLerp * Mathf.Pow(1 - timeLerp, 1) * p1.y + Mathf.Pow(timeLerp, 2) * p2.y;result.z = Mathf.Pow(1 - timeLerp, 2) * p0.z + 2 * timeLerp * Mathf.Pow(1 - timeLerp, 1) * p1.z + Mathf.Pow(timeLerp, 2) * p2.z;vectorList.Add(result);Nowtime = Nowtime + Time.deltaTime;}
}效果图如下:

最后附上二次贝塞尔曲线求导公式和正切方向计算公式:
//二次贝塞尔曲线求导公式:(1 - t)^2 * P0 + 2t(1 - t)P1 + t^2 * P2,t=[0,1]transform.position = Mathf.Pow((1 - dt), 2) * StartPos + 2 * dt * (1 - dt) * HeightPos + Mathf.Pow(dt, 2) * TargetPos;//二次贝塞尔曲线正切方向求导公式: 2t(P2 + P0 - 2*P1) + 2(P1 - P0),t=[0,1]transform.up = 2 * dt * (TargetPos + StartPos - 2 * HeightPos) + 2 * (HeightPos - StartPos);
这篇关于unity 贝塞尔曲线实例化应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




