线性方程专题

青蛙的约会——模线性方程

青蛙的约会 Time Limit:1000MS Memory Limit:10000KB 64bit IO Format:%I64d & %I64u Submit Status Practice POJ 1061 Description 两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自

$线性方程解法（齐次，非齐次）$

线性方程解法（齐次，非齐次）

转载地址：https://en.wikipedia.org/wiki/System_of_linear_equations#Solving_a_linear_system 由于很多地方需要求解齐次，非齐次线性方程，把线代，高数书毕业了都扔了，汗，简单总结一下。实际中都是用Eigen 库，调用API解线性方程组，得注意每个函数的适用条件。 where A is a

线性方程求解之二范数类型

求解线性系统在线性代数中我们经常需要求解具有m个方程，n 个未知量的问题。这个问题可以以简洁的形式表示为 Ax=b Ax=b 其中 A A 是一个m×nm\times n ， x x是一个长度为n的向量（如不特别强调，都是列向量），bb是一个长度为m 的向量。如果 m=n m = n ，并且满秩（各行向量或列向量线性无关），则这个线性方程的解为 x=A−1b x=A^{

迭代法解线性方程

迭代法是数值计算中一类典型方法，不仅用于方程求根，而且用于方程组求解，矩阵求特征值等方面。迭代法的基本思想是一种逐次逼近的方法。首先取一个精糙的近似值，然后用同一个递推公式，反复校正这个初值，直到满足预先给定的精度要求为止。对于迭代法，一般需要讨论的基本问题是：迭代法的构造、迭代序列的收敛性天收敛速度以及误差估计。迭代法的基本原理就是构造一个迭代公式，反复用

由二阶常系数线性方程的通解反推方程

由二阶常系数线性方程的通解反推方程 @(微积分) 引例是这样的：设 cosx cosx与 xex xe^x为某n阶常系数线性齐次方程的两个解，则最小的n = ？，相应的首项系数为1的方程是？分析：由cosx是一个解，则必有另一解sinx, ±i \pm i是它的特征根； xex xe^x是一个解，则必有另一解 ex e^x,则1必是二重特征根。所以，n至少为4.特征方程可以列举如

【数值计算方法】雅可比解线性方程

废话少说，直接上干货。 #include <stdio.h>#include <stdlib.h>#include <math.h>#define MaxSize 100double A[MaxSize][MaxSize]; //系数矩阵double B[MaxSize]; //系数矩阵double C[MaxSize][MaxSize]; //去对角线矩阵d

POJ 2115 C Looooops 模线性方程（扩展欧几里得）

题解：转换一下。和青蛙那题差不多。 #include<iostream>#include<cmath>using namespace std;__int64 Egcd ( __int64 a, __int64 b, __int64 &x, __int64 &y ){__int64 tmp, ret;if ( b == 0 ){x = 1, b = 0;return a;}ret = E

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，

求解模线性方程

原文：https://www.cnblogs.com/ACSeed/archive/2013/01/31/2887248.html 1）求解线性不定方程　　ax + by = c 　　先求出一组解，然后考虑如何表示通解，设d = gcd(a, b), 假设c不是d的倍数，则左边是d的倍数而右边不是，则方程无解，所以方程有解当且仅当d | c. 　　设c = c' * d,

code摘录日记[稀疏矩阵，线性方程求解迭代matlab命令] Matlab

%spy(B) %Visualize sparsity pattern of matrix% 矩阵非零元素numN = nnz(X) 线性等式求解线性方程组求解的迭代方法汇总-matlab命令 x = pcg(A,b) %preconditioned conjugate gradients method

java语言实现：数论经典问题除法表达 ,无平方因子数，直线上的点，同余与模算术大整数取模幂取模，模线性方程

package com.supermars.practice;import java.util.Scanner;public class 除法表达式 {static Scanner cin = new Scanner(System.in);public static void main(String[] args) {while (cin.hasNext()) {String s = cin

MATLAB单变量最小化函数fminbnd与非线性方程求解函数fsolve、fzero

一、函数简介 1、功能在固定间隔中找到最小的单变量函数，fminbnd是一维最小化器，它在指定的区间中找到函数最小值。 2、调用格式 x = fminbnd(fun,x1,x2) x为返回值，该值是在区间x1 <x <x2中函数的局部极小值的横坐标点；fun为函数文件、或者匿名函数； x = fminbnd(fun,x1,x2,options) 使用options中指定的优化选项最

CF 7C Line(拓展欧几里得求线性方程)

链接： http://codeforces.com/problemset/problem/7/C 题目大意：给方程Ax + By + C = 0. 其中A，B，C为已知，求x，y。分析与总结：拓展欧几里得算法的模板题。这个算法在数论书或者网上都可以找到。该算法求出线性方程Ax + By = gcd(A, B); 然后，这个方程可进行转换:

3.25每日一题（知线性常系数方程的特解求线性方程）

思路：通过特解可以知道特征根，通过特征根可以求出特征方程，通过特征方程可以求出线性方程

3.6每日一题（线性方程求通解）

1、判断类型选择方法：发现以y为未知函数，以x为自变量，不符合我们学过的类型 2、此时有两种方法：（1）x 与 y 对调，此时 x 为未知函数，y 为自变量（2）变量代换，将方程化为我们学过的类型 3、通过方法（1），我们可以发现是线性方程的类型：先化为线性方程的标准形式；再带入公式求解即可注：此时 y 为自变量

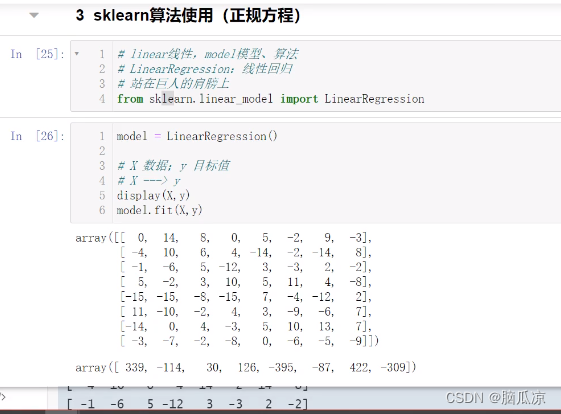
人工智能基础_机器学习003_有监督机器学习_sklearn中线性方程和正规方程的计算_使用sklearn解算八元一次方程---人工智能工作笔记0042

然后我们再来看看,如何使用sklearn,来进行正规方程的运算,当然这里首先要安装sklearn,这里如何安装sklearn就不说了,自己查一下首先我们还是来计算前面的八元一次方程的解,但是这次我们不用np.linalg.solve这个解线性方程的方式,也不用直接解正规方程的方式: 也就是上面这种方式,使用的是正规方程的形式.这个公式实现的,那么我们接下来,使用另

用matlab求线性方程的解

用矩阵除法，求线性方程组的特解利用矩阵除法求线性方程组的形式为：AX=b，其中A为系数矩阵，b为方程组右侧的一列常数。由AX=b，得X=A\b，在这种条件下，首先要保证A为满秩矩阵，否则无法求解。例如，求线性方程组的解在matlab的命令行窗口，依次输入如下命令： A=[5 4;2 5]; %系数矩阵A b=[24 13]'; %方程组右边的值 R_A

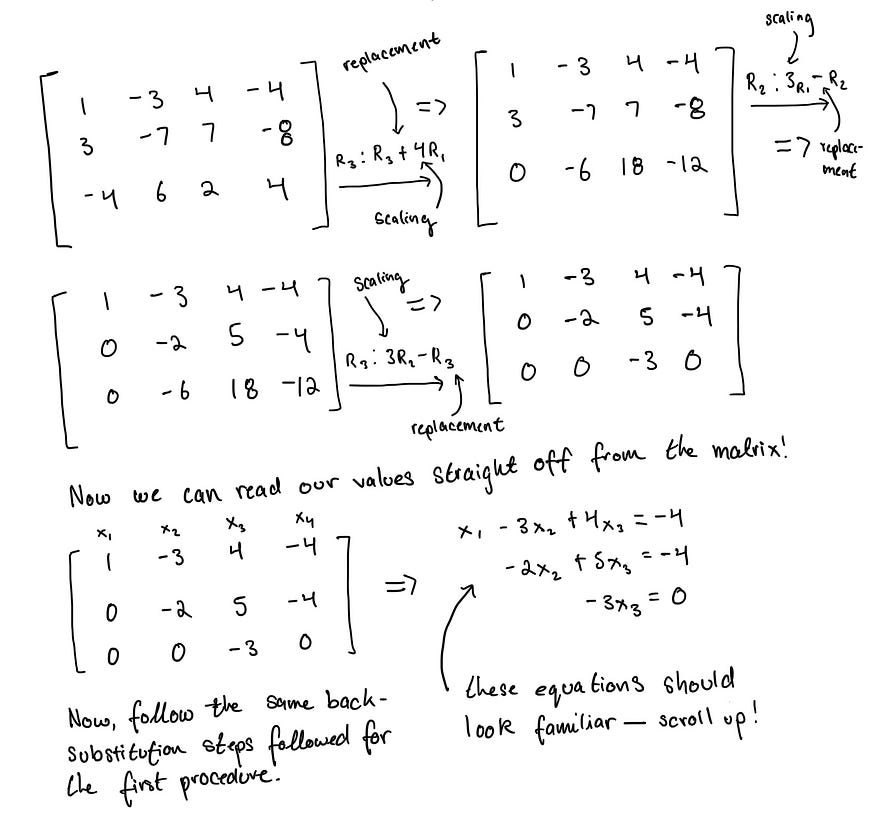
线性代数1：线性方程和系统

图片来自施泰德博物馆 Digital Collection (staedelmuseum.de) 一、前言通过这些文章，我希望巩固我对这些基本概念的理解，同时如果可能的话，通过我希望成为一种基于直觉的数学学习方法为其他人提供额外的清晰度。如果有任何错误或机会需要我进一步阐述