算法学习笔记–狄克斯特拉算法 主要内容 加权图：提高或降低某些边的权重介绍狄克斯特拉算法，能找出加权图中前往X的最短路径图中的环会导致狄克斯特拉算法不管用，如果有负权重也不适用 如果要处理负权重的图，可以使用贝尔曼-福德算法 狄克斯特算法的四个步骤 找出最便宜的节点，即可在最短时间内到达的节点对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。重复这个过程，直到对图中的

本章内容 继续图的讨论，介绍加权图------提高或降低某些边的权重。介绍狄克斯特拉算法，让你能够找出加权图中前往X的最短路径。介绍图中的环，它导致狄克斯特拉算法不管用。   在前一章，你找出了从A点到B点的路径。 这是最短路径，因为段数最少------只人三段，但不一定是最快路径。如果给这些路段加上时间，你将发现有更快的路径。 你在前一章使用了广度优先搜索，它找出的是段最少的路

使用情况 狄克斯特拉算法仅适用于有向无环图，且所有权重都是非负数。 算法步骤 1、找到从权值最“便宜”的节点，即可在最短时间(路程、花费等)内前往的节点；2、对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销；3、重复上述过程，直到对图中的每个节点都这样处理；4、计算最终路径。 Python实现 # the graphgraph = {} # 定义一个散列表#

1. 简介 广度优先算法可以找出段数最少的路径，但是对于路径上带权重的图，想要找出最快的路径，则需要使用狄克斯特拉算法。 2. 原理 为了说明狄克斯特拉算法的原理，使用换钢琴的的例子来做说明. 假设Rama想拿自己的乐谱换架钢琴： Alex说：“这是我最喜欢的乐队Destroyer的海报，我愿意拿它换你的乐谱。如果你再加5美元，还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。”Am

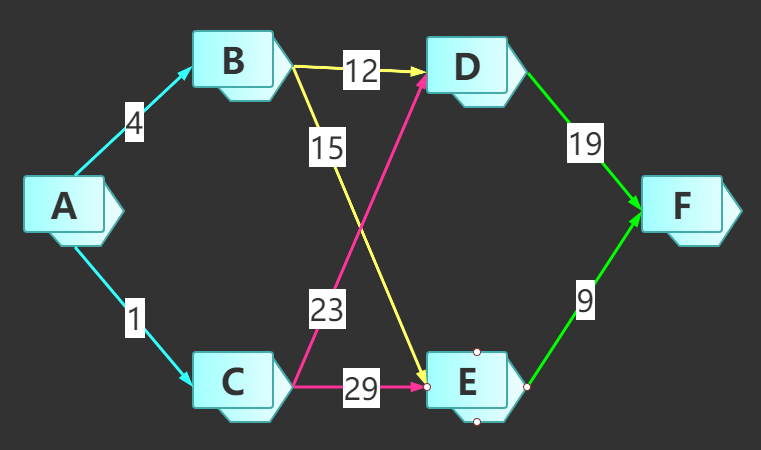
前言：此算法是解决从原点出发到其他节点的最短路径。但是也有此算法的限制条件和前提 路径是有方向且无环的路径的消耗不为负数(权重不为负数) 题目：如下图所示，从起点为A，终点为F，路径每一条边上的数字为消耗的时间权重，求A点到F点最少需要多少时间？ 题目：如下图所示，从起点为A，终点为F，经过路径上的每一条边上的数字为消耗的时间权重，求A点到F点最少需要多少时间？ file 狄克斯

图的搜索（二）：贝尔曼-福特算法、狄克斯特拉算法和A*算法 贝尔曼-福特算法 贝尔曼-福特（Bellman-Ford）算法是一种在图中求解最短路径问题的算法。最短路径问题就是在加权图指定了起点和终点的前提下，寻找从起点到终点的路径中权重总和最小的那条路径。 设置A为起点，G为终点。 首先设置各个顶点的初始权重 :起点为 0,其他顶点为无穷大(∞)。这个权重表示的是从 A 到该顶点的

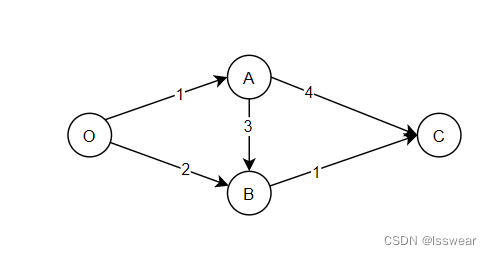
《算法图解》中提到的狄克斯特拉算法，用php实现。 一 原理及解释 根据示例图求出起点到终点的最小耗费路径。 因为涉及每条路径的权重，所以这种算法仅适合有向路径。 所谓有向路径，指仅从起点指向终点的路径。 相对的无向路径，指起点和终点互相指向的路径，一般这样的路径不带箭头。 该算法设定每条路径没有权重为负的路径，且没有不可指向终点的路径，所以所有节点都有效。 起点“O”，终点“C”，