本文主要是介绍算法图解 第7章 狄克斯特拉算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本章内容
- 继续图的讨论,介绍加权图------提高或降低某些边的权重。
- 介绍狄克斯特拉算法,让你能够找出加权图中前往X的最短路径。
- 介绍图中的环,它导致狄克斯特拉算法不管用。
在前一章,你找出了从A点到B点的路径。
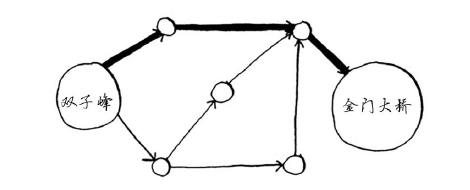
这是最短路径,因为段数最少------只人三段,但不一定是最快路径。如果给这些路段加上时间,你将发现有更快的路径。

你在前一章使用了广度优先搜索,它找出的是段最少的路径(如第一个图所示)。如果你要找出最快的路径(如第二个图所示),该如何办呢?为此,可使用另一处算法------狄克斯特拉算法(Dijkstra's algorithm)。
7.1 使用狄克斯特拉算法
下在来看看如何对下面的图使用这种算法。
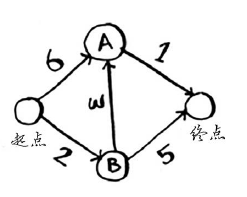
其中每个数字表示的都是时间,单位分钟。为找出从起点到终点耗时最短的路径,你将使用锹克斯特拉算法。
如果你使用广度优先搜索,将得到下面这条段数最少的路径。
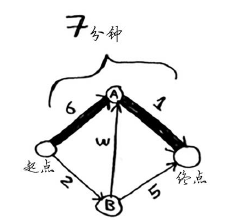
这条路径耗时7分钟。下面来看看能否找到耗时更短的路径!狄克斯特拉算法包含4个步骤。
(1)找出“最便宜”的节点,即可在最短时间内到达的节点。
(2)更新该节点的邻居的开销,其含义稍后介绍。
(3)重复这个过程,直到对图中的每个节点都这样做了。
(4)计算最终路径。
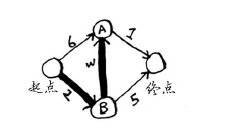
第一步:找出最便宜的节点。你站在起点,不知道该前往节点A还是前行节点B。前往这两个节点都要多长时间呢?
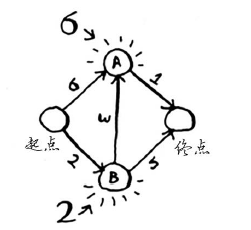
前往节点A需要6分钟,而前往节点B需要2分钟。至于前行其他节点,你还不知道需要多长时间。
由于你还不知道前往终点需要多长时间,因此你假设为无穷大(这样做的原因你马上就会明白)。节点B是最近的----2分钟就能达到。
第二步:计算经节点B前往其各个邻居所需的时间
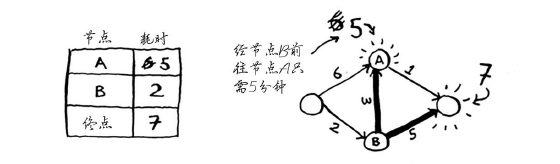
第二步:计算经节点B前往其各个邻居所需要的时间。
你刚找到了一条前往节点A的更短路径!直接前往节点A需要6分钟。
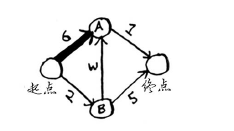
但经由节点B前往A只需要5分钟!
对于 节点B的邻居,如果找到前往它的更短路径,就更新其开销。在这里,你找到了:
前往节点A的更短路径(时间从6分钟缩短到5分钟);
前往终点的更短路径(时间从无穷大缩短到7分钟)。
第三步:重复!
重复第一步:找出可在最短时间内前往的节点。你对节点B执行了第二步,除节点B外,可在最短时间内前往终点的节点是节点A。
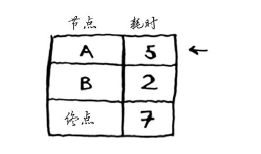
重复第二步:更新节点A的所有邻居的开销。
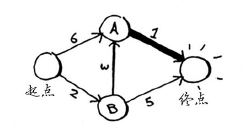
你发现前往终点的时间为6分钟!
你对每个节点都运行了狄克斯特拉算法(无需对终点这样做)。现在,你知道:
前往节点B需要2分钟;
前往节点 A需要5分钟;
前往终点需要6分钟。
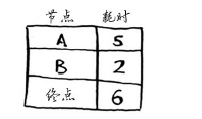
最后一步------计算最终路径将留到下一节去介绍。
7.2 术语
介绍其他狄克斯特拉算法使用示例前,先来澄清一些术语。
狄克斯特拉算法用于每条边都有关联数字的图,这些数字乐为权重(weight)。
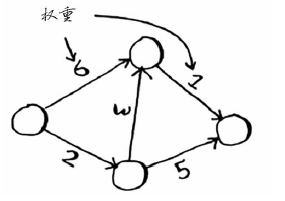
带权重的图称为加权图(weighted graph),不带权重的图称为非加权图(unweighted graph)。
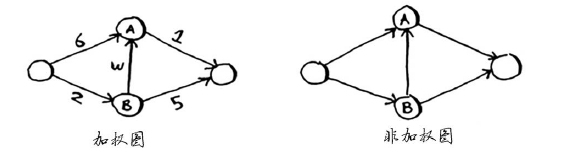
要计算非另权图中的最短路径,可使用广度优先搜索。要计算加权图中的最短路径,可使用狄克斯特拉算法。图学可能有环,而环类似右面这样。
这意味着你可以从一个节点出发,走一圈后又回到这个节点。假设在下面这个带环图中,你要找出从起点到终点的最短路径。

绕环前行是否合理呢?你可以选择避开环的路径。
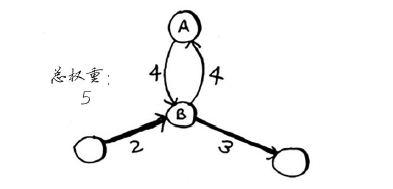
也可以选择包含环的路径。
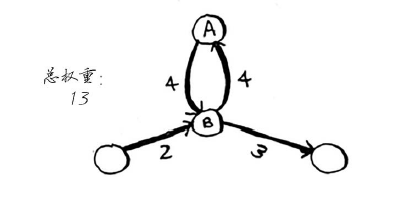
这两条路径都可到达终点,但环增加了权重。如果你愿意,甚至可绕环两次。
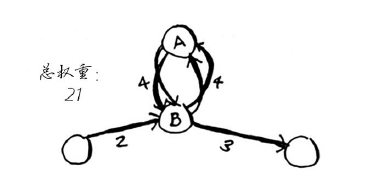
但每绕环一次,总权重都增加8.因此,绕环的路径不可能是最短的路径。
最后,还记得第6章对有向图和无向图的讨论吗?

无向图意味着两个节点彼此指向对方,其实就是环!
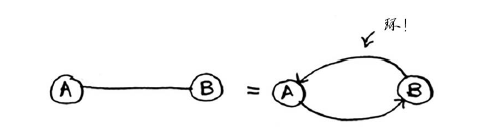
在无向图中,每条边都是一个环。狄克斯特拉算法只适用有向无环图(directed acyclic graph,DAG)。
7.3 换钢琴
术语介绍得差不多了,我们来看一个例子!这是Rama,想拿一本乐谱换架钢琴。
Alex说:“这是我最喜欢的乐队Destroyer的海报,我愿意拿它换你的乐谱。如果你再加5美元,还可拿乐谱换我这张稀有的Rick Astley 黑胶唱片。" Amy说:"哇,我听说这张黑胶唱片里有首非常好听的歌曲,我愿意拿我的吉他或架子鼓换这张海报或黑胶唱片。"
Beethoven惊呼:”我一直想要吉他,我愿意拿我的钢琴换Amy的吉他或架子鼓。“
太好了!只要再花一点钱,Rama就能拿乐谱换架钢琴。现在他需要确定的是,如何花最少的钱实现这个目标。我们来绘制一个图,列出大家的交换意愿。

这个图中的节点是大家愿意拿出来交换的东西,边的权重是交换时需要额外加多少钱。拿海报换吉他需要额外加30美元,拿黑胶唱片换吉他需要额外加15美元。Rama 需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。为此,可以使用狄克斯特拉算法!别忘了,狄克斯特拉算法包含四个步骤。在这个示例中,你将完成的有这些步骤,因此你了将计算最终路径。动手之前,你需要做些准备工作:创建一个表格,在其中列出每个节点的开销。这里的开销指的是达到节点需要额外支付多少钱。

在执行狄克斯特拉算法的过程中,你将不断更新这个表。为计算最终路径,还需在这个表中添加表示父节点的列。
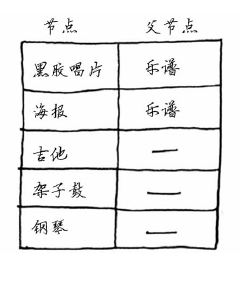
这列的作用将稍后介绍。我们开始执行算法吧。
每一步:找出最便宜的节点。在这里,换海报最便宜,不需要支付额外的费用。不家更便宜的换海报的途径吗?这一点非常重要,你一定要想一想。Rama能够通过一系列交换得到海报,还能额外得到钱吗?想清楚后接着往下读。答案是不能,因为海报是Rama能够到达的最便宜的节点,没法再便宜了。下面提供了另种思考角度。假设你要从家里去单位。
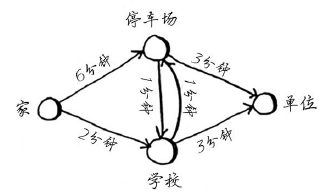
如果你走经过学校的路,到学校需要2分钟。如果你走经过停车场的路,到停车场需要6分钟。如果经停车场前行学校,能不能将时间缩短到少于2分钟呢?不可能,因为只前往停车场就超过2分钟了。另一方面,有没有能更快到达停车场的路呢?有。

这就是狄克斯特拉算法背后的关键理念:找出图中最便宜的节点,并确保没有到该节点的更便宜的路径!
回到换钢琴的例子。换海报需要支付的额外费用最少。
第二步:计算前往该节点的各个邻居的开销。

现在的表中包含低音吉他和架子鼓的开销。这些开销是用海报交换它们时需要支持的额外费用。因此父节点为海报。这意味着,要到达低音吉他,需要沿从海报出发的边前行,对架子鼓来说亦如此。

再次执行第一步:下一个最便宜的节点是黑胶唱片------需要额外支付5美元。
再次执行第二步:更新黑胶唱片的各个邻居的开销。

你更新了架子鼓和吉他的开销!这意味着经”黑胶唱片“前往”架子鼓“和”吉他“的开销更低,因此你将这些乐器的父节点改为黑胶唱片。
下一个最便宜的是吉他,因此更新其邻居的开销。

你终于计算出了用吉他换钢琴的开销,于是你将其父节点设置为吉他。最后,对最后一个节点---架子鼓,做同样的处理。

如果用架子鼓换钢琴,Rama需要额外支付的费用更少。因此,采用最便宜的交换路径时,Ramma需要额外支付35美元。
现在来兑现前面的承诺,确定最终的路径。当前,我们知道最短路径的开销为35美元,但如何确定这条路径呢?为此,先找出钢琴的父节点。

钢琴的父节点为架子鼓,这意味着Rama需要用架子鼓来换钢琴。因此你就沿着这一边。
我们来看看需要沿着哪些边前行。钢琴的父节点为架子鼓。

驾子鼓的父节点为黑胶唱片。

因此Rama需要用黑胶唱片换架子鼓。显然,他需要用乐谱来换黑胶唱片。。通过沿父节点回溯,便得到了完整的交换路径。

下面是Rama需要做的一系列交换。

本章前面使用的都是术语最短路径的字面意思:计算两点或两人之间的最短路径。但希望这个示例让你明白:最短路径指的并不一定是物理距离,也可能是让某种度量指标最小。在这个示例中,最短路径指的是Rama想要额外支付的费用最少。这都要归功于锹克斯特拉!
7.4 负权边
在前面的交换示例中,Alex提供了两种可用乐谱交换的东西。
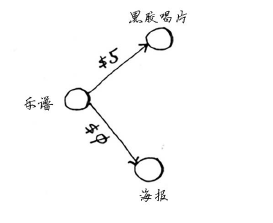
假设黑胶唱片不是Alex的,而是Sarah的,且Sarah愿意用黑胶唱片和7美元换海报。换句话说,换得Alex的海报后,Rama用它来换Sarah的黑胶唱片时,不但不用支付额外的费用,还可得7美元。对于这种情况,如何在图中表示出来呢?

从黑胶唱片到海报的边的权重为负!即这种交换让Rama能够得到7美元。现在,Rama有两种获得海报的方式。

第二种方式的开销少2美元,他就采取这种方式。然而,如果你对这个图运行狄克特拉算法,Rama将选择错误的路径-----更长的那条路径。如果有负权边,就不能使用狄克斯特拉算法。因为负权边会导致这种算法不管用。下面来看看这个图执行狄克斯特拉算法的情况。首先,创建开销表。
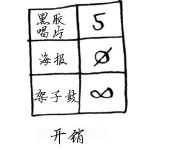
接下来,找出开销最低的节点,并更新其邻居的开销。在这里,开销最低的节点是海报。根据狄克斯特拉算法,没有比不支付任何费用获得海报更便宜的方式。(你知道这并不对!)无论如何,我们来更新其邻居开销。
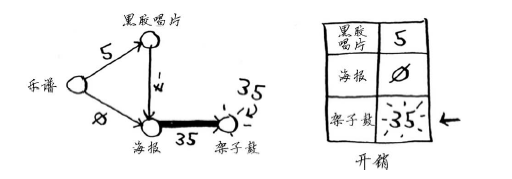
现在,架子鼓的开销变成了35美元。
我们来找出最便宜的未处理节点。
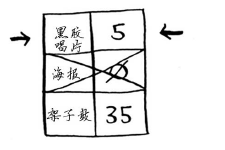
更新其邻居的开销。
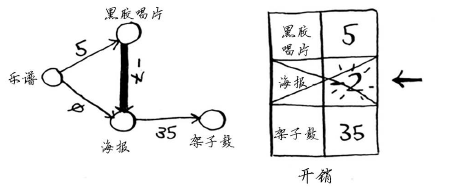
海报节目已处理过,这里却更新了它的开销。这是一个危险信号。节点一旦被处理,就意味着没有前往该节点的更便宜途径,但你刚才却找到了前往海报节点的更便宜途径!架椰鼓没有任何邻居,因此算法到此结束,最终开销如下。
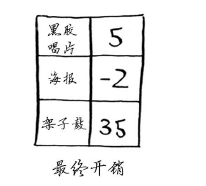
换得架子鼓的开销为35美元。你知道有一种交换方式只需要33美元,但狄克斯特拉算法没有找到。这是加为狄克斯特拉算法这样假设:对于处理过的海报节点,没有前往该节点的更短路径。这处假设公在没有负权边时才成立。因此,不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中,要找出最短路径,可使用另一处算法------贝乐曼-福德算法(Bellman-Ford algorithm)。本书不介绍这种算法,你中以在网上找到其详尽的说明。
7.5 实现
下面来看看如何使用代码来实现狄克斯特拉算法,这里以下面的图为例。

要编写解决这个问题的代码,需要三个散列表。

随着算法的进行,你将不断更新散列表consts和parents。首先需要实现这个图,为此可像第6章那样使用一个散列表。
graph = {}
在前一章中,你像下面这样将节点的所有邻居都存储在散列表中。
graph["ypu"] = ["alice","bob","claire"]
但这里需要同时存储邻居和前往邻居的开销。例如,起点有两个邻居---------A和B。
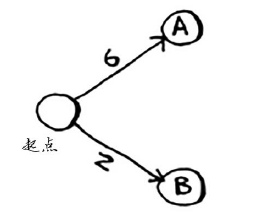
如何表示这些边的权重呢?为何不使用另一个散列表呢?
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

因此graph["start"] 是一个散列表。要获取起点的所有邻居,可像下面这样做。
>>> print graph["start"].keys()
["a","b"]
有一条从起点到A的边,还有一条从起点到B的边。要获悉这此边的权重,该如何办呢?
>>> print graph["start"]["a"]
2
>>> print graph["start"]["b"]
6
下面来添加其亿节点及其邻居。
graph['a'] = {}
grapn["a"]["fin"] = 1
graph["b"] ={}
graph["b"]["a"] = 3
graphn["b"]["fin"] = 5
graph["fin"] = {} <—————终点没有任何邻居。

接下来,需要用一个散列表来存储每个节点的开销。
节点的开销指的是从起点出发前往该节点需要多长时间。你知道的,从起点到节点B需要2分钟,从起点到节点A需要6分钟(但你可能会找到所需要时间更短的路径)。你不知道到终点需要多长时间。对于学不知道的开销,你将其设置为无穷大。在Phthon中能够表示无穷大吗?你可以这样做:
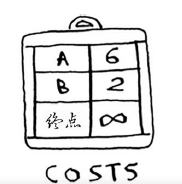
infinity = float("inf")
创建开销表的代码如下:
infinity = float("inf")
consts = {}
const["a"] = 6
const["b"] = 2
consts["fin"] = infinity
还需要一个存储父节点的散列表:
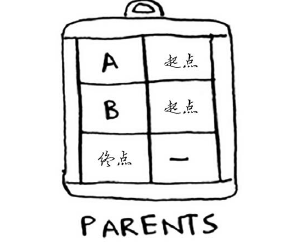
创建这个散列表的代码如下:
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
最后,你需要一个数组,用于记录处理过的节点,因为对于同一个节点,你不用处理多次。
processed = []
准备工作做好了,下面来看看算法。

我先列出代码,然后再详细介绍。代码如下。
#在未处理的节点中找出开销最小的节点
node = find_lowest_cost_node(consts)
while node is not None: #这个while循环在所有节点都被处理过后结束const = consts[node]neighbors = graph[node]for n in neighbors.keys(): #遍历当前节点所有邻居new_cost = cost + neighbors[n]if const[n] > new_cost: #如果经当前节点前往邻居更近,const[n] = new_cost #就更新该邻居的开销parents[n] = node #同时将该邻居的父节点设置为当前节点processed.append(node) #即当前节点标记为处理过node = find_lowest_const_node(consts) #找出接下来要处理的节点,并循环这就是实现狄克斯特拉算法的Python代码!函数find_lowest_const_node的代码稍后列出,我们先来看看这些代码的执行过程。
找出开销最低的节点。

获取该节点的开销和邻居。

遍历邻居。
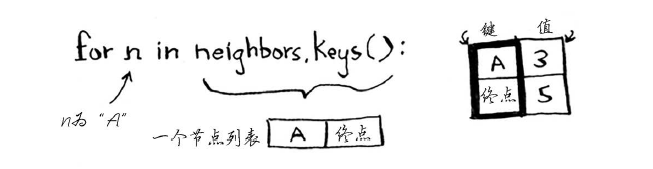
每个节点都有开销。开乐指的是从起点前往该节点需要多长时间。在这里,你计算从起点出发,经节点B前往节点A(而不是直接前往节点A)需要多长时间。

接下来对新旧开销进行比较。

找到了一条前往节点A的更短路径!因此更新节点 A的开销。

这条新路径经由节点B,因此节点A的父节点改为节点B。

现在回到了for循环开头。 下一下邻居是终点节点。
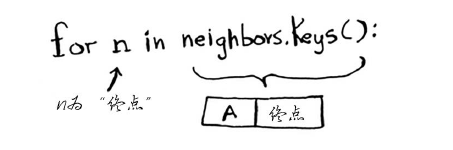
经节点B前往终点需要多长时间呢?
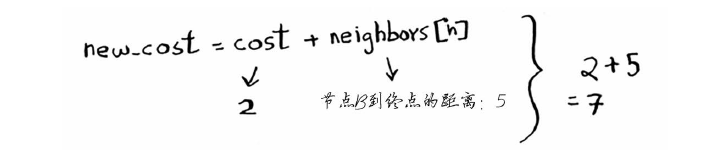
需要7分钟。终点原来的开销为无穷大,比7分钟长。

设置终点节点的开销和父节点。

你更新了节点B的所有邻居的开销。现在,将节点B标记为处理过。

找出接下来要处理的节点。

获取节点A的开销和邻居。

节点A只有一个邻居:终点节点。

当前,前往终点需要7分钟。如果经节点A前往终点,需要多长时间呢?

经节点A前往终点所需的时间更短!因此更新终点的开销和父节点。

处理所有的节点后,这个算法就结束了。希望前面对执行过程的详细介绍让你对这个算法有更深入的认识。函数find_lowest_const_node找出开销最低的节点,其代码非常简单,如下所示。
def find_lowest_cost_node(costs):lowest_cost = float("inf")lowest_cost_node = Nonefor node in costs: #遍历所有节点cost = costs[node]if cost < lowest_cost and node not in processed: #如果当前节点的开销更低且未处理过,就将其视为开销最低的节点lowest_cost = costslowest_cost_node = nodereturn lowest_cost_node7.6 小结
广度优先搜索用于在非加权图查找最短路径。
狄克斯特拉算法用于在加权图中查找最短路径。
仅当权重为正时狄克斯特拉算法才管用。
如果图中包含负权边,请使用贝乐曼-福德算法。
这篇关于算法图解 第7章 狄克斯特拉算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









