狄克斯特拉算法(Dijkstra算法)---单源最短路径问题

前言：此算法是解决从原点出发到其他节点的最短路径。但是也有此算法的限制条件和前提

• 路径是有方向且无环的
• 路径的消耗不为负数(权重不为负数)

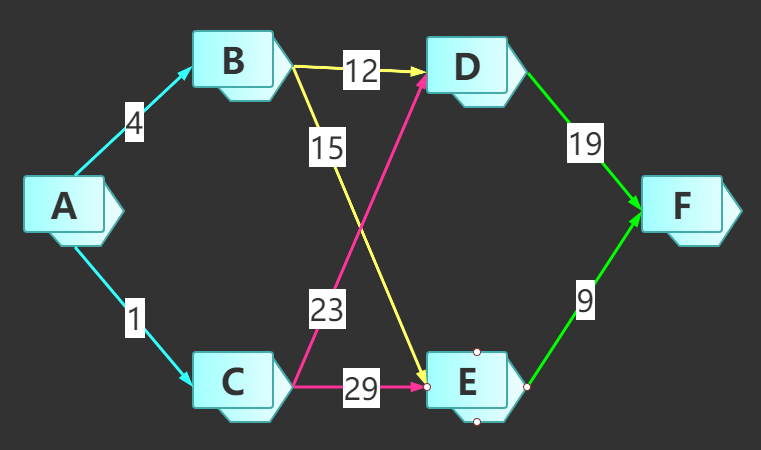
题目：如下图所示，从起点为A，终点为F，路径每一条边上的数字为消耗的时间权重，求A点到F点最少需要多少时间？

题目：如下图所示，从起点为A，终点为F，经过路径上的每一条边上的数字为消耗的时间权重，求A点到F点最少需要多少时间？

file

狄克斯特拉算法按照如下规则运行

1. 找出目前知道的最便宜的节点，即最短时间内到达的节点(不知道的节点算无穷大，如：D、E、F)。
2. 更新对应最便宜节点相邻节点的开销。
3. 对图中的每个节点都执行第一步和第二步，直到没有节点可执行为止。
4. 计算最终节点

示例代码如下：

using System.Collections.Generic;
using UnityEngine;public class DijkstraAlgorithm : MonoBehaviour
{/// <summary>/// 相当于Main函数/// </summary>void Start(){InvokeDijkstra();}/// <summary>/// 对应的节点到周围节点需要的时间(权重)/// </summary>private Dictionary<string, Dictionary<string, float>> graphDictionary = new Dictionary<string, Dictionary<string, float>>();/// <summary>/// 从原点到指定节点需要的时间(权重)/// </summary>private Dictionary<string, float> sourceToNodeCost = new Dictionary<string, float>();/// <summary>/// 节点对应的父节点/// </summary>private Dictionary<string, string> nodeParentDictionary = new Dictionary<string, string>();/// <summary>/// 已经处理过的节点集合，此处理更新对应最便宜节点相邻节点的开销/// </summary>private List<string> processedNodeList = new List<string>();public void InvokeDijkstra(){//初始化节点和对应邻居节点的数据结构graphDictionary.Add("A", new Dictionary<string, float>());graphDictionary.Add("B", new Dictionary<string, float>());graphDictionary.Add("C", new Dictionary<string, float>());graphDictionary.Add("D", new Dictionary<string, float>());graphDictionary.Add("E", new Dictionary<string, float>());graphDictionary.Add("F", new Dictionary<string, float>());//添加对应的节点到邻居节点的花销graphDictionary["A"].Add("B", 4.0f);graphDictionary["A"].Add("C", 1.0f);graphDictionary["B"].Add("D", 12.0f);graphDictionary["B"].Add("E", 15.0f);graphDictionary["C"].Add("D", 23.0f);graphDictionary["C"].Add("E", 429.0f);graphDictionary["D"].Add("F", 19.0f);graphDictionary["E"].Add("F", 9.0f);//原点是第一个节点，所以花费为0sourceToNodeCost.Add("A", 0);var lowestConstNodeName = FindLowestConstNode(sourceToNodeCost);while (!string.IsNullOrEmpty(lowestConstNodeName)){//找到对应的邻居foreach (var node in graphDictionary[lowestConstNodeName]){//节点的总体花费 = 原点到父节点的总体花费 + 父节点到此节点的花费float tempCost = sourceToNodeCost[lowestConstNodeName] + node.Value;float originalCost = sourceToNodeCost.ContainsKey(node.Key) ? sourceToNodeCost[node.Key] : float.PositiveInfinity;if (tempCost< originalCost){sourceToNodeCost[node.Key] = tempCost;nodeParentDictionary[node.Key] = lowestConstNodeName;}}//此节点已经完成处理processedNodeList.Add(lowestConstNodeName);//查找下一个花费最少并且没有处理的节点lowestConstNodeName = FindLowestConstNode(sourceToNodeCost);}var fullPath = ShortestPath("F");Debug.Log($"最短的路径为：{fullPath}");}/// <summary>/// 发现时间最少且没有被处理的节点/// </summary>/// <returns></returns>public string FindLowestConstNode(Dictionary<string, float> sourceToNodeCost){float tempValue = float.PositiveInfinity;string nodeName = "";foreach (var node in sourceToNodeCost){if (!processedNodeList.Contains(node.Key)){if (node.Value < tempValue){tempValue = node.Value;nodeName = node.Key;}}}return nodeName;}public string ShortestPath(string finalNodeName){string result = "";if (nodeParentDictionary.ContainsKey(finalNodeName)){result += ShortestPath(nodeParentDictionary[finalNodeName]);result += finalNodeName + " --> ";}else{result += finalNodeName + " --> ";}return result;}
}