本文主要是介绍狄克斯特拉(Dijkstra) 算法 php实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《算法图解》中提到的狄克斯特拉算法,用php实现。
一 原理及解释
根据示例图求出起点到终点的最小耗费路径。
因为涉及每条路径的权重,所以这种算法仅适合有向路径。
所谓有向路径,指仅从起点指向终点的路径。
相对的无向路径,指起点和终点互相指向的路径,一般这样的路径不带箭头。
该算法设定每条路径没有权重为负的路径,且没有不可指向终点的路径,所以所有节点都有效。
起点“O”,终点“C”,实例图如下
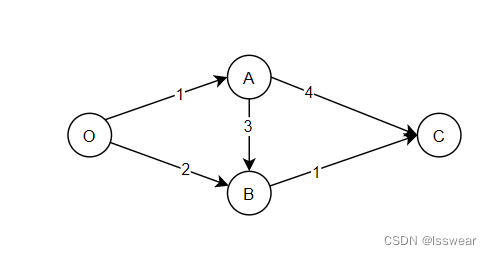
根据图示,路径0到A耗费1总耗费1记作A<-O:1:1,以此类推B<-O:2:1,选取耗费最小的路径A<-O:1:1,此时O节点遍历完成。
从节点A再次开始C->A:4,总耗费需要加上之前路径的耗费所以C->A:4:5,A节点遍历完成。
剩余B节点未处理,选取B节点开始C->B:1:3,B节点遍历完成。因为总消耗3小于总消耗5,所以选择C->B路径。
因为C节点是终点,不用便利。所以其余节点遍历完成,则C节点处理完成。
最终选择路径O->B->C,总消耗3。
二 处理流程
1、初始化
| 节点 | 总耗费 | 父节点 | 遍历完成 |
| O | FALSE | FALSE | FALSE |
| A | FALSE | FALSE | FALSE |
| B | FALSE | FALSE | FALSE |
| C | FALSE | FALSE | FALSE |
2、选取起点节点O
| 节点 | 总耗费 | 父节点 | 遍历完成 |
| O | FALSE | FALSE | TRUE |
| A | 1 | O | FALSE |
| B | 2 | O | FALSE |
| C | FALSE | FALSE | FALSE |
下一步,选取耗费最少且未遍历完成的节点,但是要注意耗费的值不能是FALSE。可将耗费中FALSE视为最大。
某些语言中有无穷大的常量关键字,可以直接用大小对比排除未设置耗费数量的节点。
3、选取节点A
| 节点 | 总耗费 | 父节点 | 遍历完成 |
| O | FALSE | FALSE | TRUE |
| A | 1 | O | TRUE |
| B | 2 | O | FALSE |
| C | 4 | A | FALSE |
B->A:3:4,原有节点总耗费为2,小于4。所以不采用B->A,即B->A的数据不更新到表中。
下一步,选取耗费最少且未遍历完成的节点。
4、选取节点B
| 节点 | 总耗费 | 父节点 | 遍历完成 |
| O | FALSE | FALSE | TRUE |
| A | 1 | O | TRUE |
| B | 2 | O | TRUE |
| C | 3 | B | TRUE |
B->C:1:3,原有节点总耗费为4,大于3。所以采用C->B,即C->B的数据更新到表中。
此时除去终点的节点都处理完,代表终点处理完成,即节点C处理完成。
5、处理流程总结
1、初始化表
2、选取起点节点
3、开始首次处理,即是用节点数据更新表数据
4、设置节点处理完成
5、选取耗费最少且未遍历完成的节点
6、重复4、5步操作。当节点为终点节点时推出循环
7、生成结果
三 php实现
//狄克斯特拉(Dijkstra) 算法 实现
class Test
{/*** $tableitem =['node'=>'','cost'=>'','prev'=>'']*/private $table = []; //计算开销数据private $result = []; //结算表private $data = [];private $start;private $end;public function __construct($data, $start, $end){$this->data = $data;$this->start = $start;$this->end = $end;}private function insert_tables($data){foreach ($data as $key => $value) {$this->insert_table($key);if (is_array($value)) {$this->insert_tables($value);}}}/*** 向table加数据** @param [type] $node* @return void* @author wj* @date 2023-10-18*/private function insert_table($node){if (!isset($this->table[$node])) {$this->table[$node] = ['node' => $node,'cost' => false,'prev' => false,'isChecked' => false,];}}/*** 改table数据** @param [type] $node* @param [type] $cost* @param [type] $prev* @return void* @author wj* @date 2023-10-18*/private function update_table($node, $cost, $prev){$info = $this->table[$node];if ($cost < $info['cost'] || false == $info['cost']) {$this->table[$node]['cost'] = $cost;$this->table[$node]['prev'] = $prev;}}/*** 处理节点** @param boolean $node* @return void* @author wj* @date 2023-10-18*/private function deal_node($node = false){if (empty($node)) {$node = $this->get_need_deal_node();}if (empty($node) || !isset($this->data[$node])) {return false;}$usedata = $this->data[$node];$prev = $node;$table_cost = $this->table[$prev]['cost'];foreach ($usedata as $key => $cost) {$totalcost = $cost + (int) $table_cost;$this->update_table($key, $totalcost, $prev);}$this->table[$node]['isChecked'] = true;return true;}/*** 取得最小未处理节点** @param [type] $node* @return void* @author wj* @date 2023-10-18*/private function get_need_deal_node(){$table = $this->table;$min_node = false;$cost = false;foreach ($table as $key => $value) {if ($value['isChecked'] || false === $value['cost']) {continue;}if ($value['cost'] < $cost || false === $cost) {$cost = $value['cost']; //最小开销$min_node = $key;}}return $min_node;}/*** 设定data 无没用分支 没有负权** @param [type] $data* @param [type] $start* @param [type] $end* @return void* @author wj* @date 2023-10-18*/public function dotest(){//初始化table;$this->insert_tables($this->data);$node = $this->start;//处理节点while ($node) {$result = $this->deal_node($node);$node = $this->get_need_deal_node();if ($node == $this->end) {$this->table[$this->end]['isChecked'] = true;break;}}}public function getresult(){$end = $this->end;$result = [];$node = $end;while ($node) {$nodeinfo = $this->table[$node];$result[$nodeinfo['node']] = $nodeinfo;$node = $nodeinfo['prev'];}$result = array_reverse($result);$path = implode("->", array_keys($result));$lastnode = end($result);$cost = $lastnode['cost'];$data = ['result' => $result,'path' => $path,'cost' => $cost,];return $data;}
}
$data = ["O" => ["A" => 0,"B" => 1,],"A" => ["C" => 1,"B" => 2,],"B" => ["D" => 2,],"C" => ["D" => 3,],
];
$t = new Test($data, "O", "D");
$t->dotest();
$data = $t->getresult();
var_dump($data);#执行结果
array(3) {'result' =>array(3) {'O' =>array(4) {'node' =>string(1) "O"'cost' =>bool(false)'prev' =>bool(false)'isChecked' =>bool(true)}'B' =>array(4) {'node' =>string(1) "B"'cost' =>int(1)'prev' =>string(1) "O"'isChecked' =>bool(true)}'D' =>array(4) {'node' =>string(1) "D"'cost' =>int(3)'prev' =>string(1) "B"'isChecked' =>bool(true)}}'path' =>string(7) "O->B->D"'cost' =>int(3)
}这篇关于狄克斯特拉(Dijkstra) 算法 php实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






