步长专题
H.264量化参数QP和量化步长Qstep
1. 量化参数QP是量化步长Qstep的序号。对于亮度(Luma)编码而言,量化步长Qstep共有52个值,QP取值0~51,对于色度(Chroma)编码,Q的取值0~39。 QP取最小值0 时,表示量化最精细;相反,QP取最大值51时,表示量化是最粗糙的。 QP和Qstep具有线性相关性,Qstep随着QP的增加而增加,每当QP值增加6,Qstep便增加一倍。 量化是在
python计算开始时间到结束时间步长一个小时
为了计算从开始时间到结束时间,每隔一小时的时间间隔,你可以使用Python的datetime模块来处理日期和时间。以下是一个简单的例子,它生成从开始时间到结束时间每隔一小时的时间列表。 from datetime import datetime, timedelta# 开始时间start_time_str = '2023-03-01 08:00:00'start_time = datetim
理解CNN参数及PyTorch实例,卷积核kernel,层数Channels,步长Stride,填充Padding,池化Pooling,PyTorch中的相关方法,MNIST例子
1.34.理解CNN参数及PyTorch实例 1.34.1.卷积核kernel 1.34.2.层数Channels 1.34.3.步长Stride 1.34.4.填充Padding 1.34.5.池化Pooling 1.34.6.PyTorch中的相关方法 1.34.7.MNIST例子 1.34.理解CNN参数及PyTorch实例 参考地址:http://guileen.github.io/2
基于长短期记忆神经网络LSTM的多步长时间序列预测
基于长短期记忆神经网络LSTM的多步长多变量时间序列预测 长短时记忆网络(LSTM)是一种能够学习和预测长序列的递归神经网络。LSTMs除了学习长序列外,还可以学习一次多步预测,这对于时间序列的预测非常有用。LSTMs的一个困难在于,它们可能难以配置,而且需要大量的准备工作才能获得适合学习的格式的数据。 在本教程中,您将了解如何使用Keras在Python中开
父类指针的步长和子类指针的步长是不一样的
当用父类指针或者引用指向子类对象时,可以发生多态(是因为有vptr指针和虚函数表的存在),但是这个指针和子类指针的步长时不一样,具体看如下代码,特别注意看注释。 代码如下: #include <iostream>using namespace std;//结论://多态是用父类指针指向子类对象 和 父类步长++,是两个不同的概念class Parent{public:Parent(in
YOLOv9独家原创改进|增加SPD-Conv无卷积步长或池化:用于低分辨率图像和小物体的新 CNN 模块
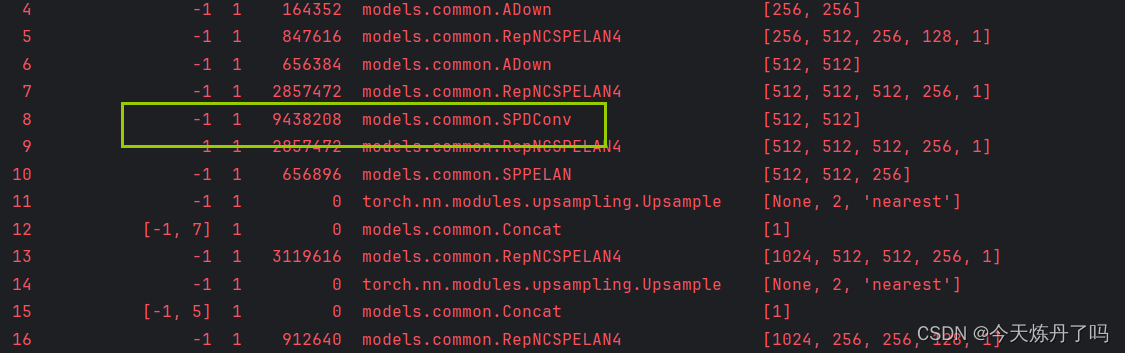
专栏介绍:YOLOv9改进系列 | 包含深度学习最新创新,主力高效涨点!!! 一、文章摘要 卷积神经网络(CNNs)在计算即使觉任务中如图像分类和目标检测等取得了显著的成功。然而,当图像分辨率较低或物体较小时,它们的性能会灾难性下降。这是由于现有CNN常见的设计体系结构中有缺陷,即使用卷积步长和/或池化层,这导致了细粒度信息的丢失和较低效的特征表示的学习。为此,
YOLOv9改进|增加SPD-Conv无卷积步长或池化:用于低分辨率图像和小物体的新 CNN 模块
专栏介绍:YOLOv9改进系列 | 包含深度学习最新创新,主力高效涨点!!! 一、文章摘要 卷积神经网络(CNNs)在计算即使觉任务中如图像分类和目标检测等取得了显著的成功。然而,当图像分辨率较低或物体较小时,它们的性能会灾难性下降。这是由于现有CNN常见的设计体系结构中有缺陷,即使用卷积步长和/或池化层,这导致了细粒度信息的丢失和较低效的特征表示的学习。为此,
tensorflow中卷积神经网络中 步长stride的定义
在tensorflow中,卷积神经网络的使用方法如下: tf.nn.conv2d(input, filter, striders, padding, use_cudnn_on_gpu=None, name=None) 其中,步长stride是一个一维的向量,长度为4。 形式是[a,x,y,z],分别代表[batch滑动步长,水平滑动步长,垂直滑动步长,通道滑动步长] 在tensorf
图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化
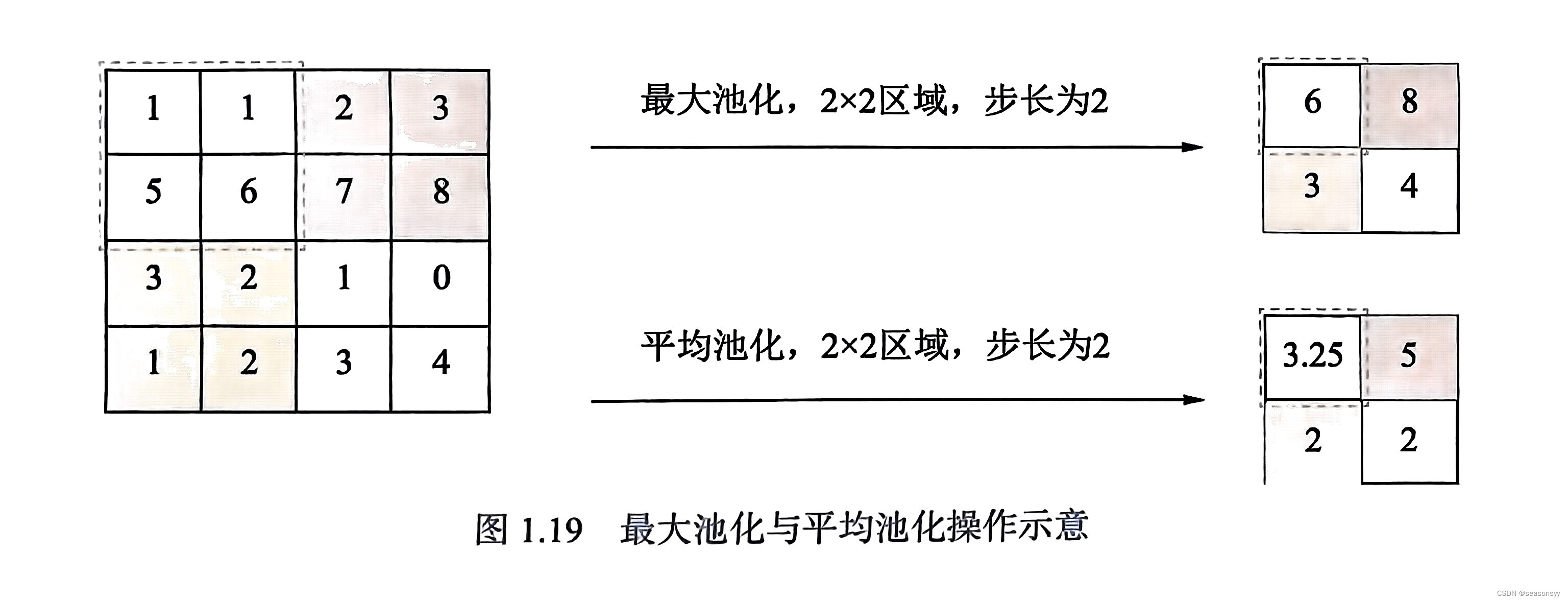
图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化 卷积神经网络的一些基本概念:图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化 1.图像卷积、步长、填充 图像卷积:卷积核矩阵在一个原始图像矩阵上 “从上往下、从左往右”滑动窗口进行卷积计算,然后将所有结果组合到一起得到一个新的矩阵的过程。(图1.13) 用一个相同的卷积核对整幅图像进行进行卷积操作,相当于
C++中父子类中指针的步长问题
#include <iostream>using namespace std;class Parent{public:Parent(int a=0){this->a = a;}virtual void print(){cout << "我是爹" << endl;}private:int a;};class Child:public Parent{public:Child(int a
非精线搜索步长规则Armijo规则Goldstein规则Wolfe规则
非精确线搜索步长规则 在数值优化中,线搜索是一种寻找合适步长的策略,以确保在目标函数上获得足够的下降。如最速下降法,拟牛顿法这些常用的优化算法等,其中的线搜索步骤通常使用Armijo规则、Goldstein规则或Wolfe规则等。 设无约束优化问题: min f ( x ) , x ∈ R n \min f(x),{\kern 1pt} \,x \in {R^n} minf(x),x∈R
rust for循环步长-1,反向逆序遍历
fn main() {for i in (0..3).rev().step_by(1) {print!("{}", i);}}// 打印结果:210 Trait std::iter::Iterator fn rev(self) -> Rev where Self: Sized + DoubleEndedIteratorfn step_by(self, step: usize) -> St
脉冲神经网络(SNN)论文阅读(五)-----AAAI-2024 时间步长逐渐收缩的SNN
原文链接:CSDN-脉冲神经网络(SNN)论文阅读(五)-----AAAI-2024 时间步长逐渐收缩的SNN Shrinking Your TimeStep: Towards Low-Latency Neuromorphic Object Recognition with Spiking Neural Networks 目录论文信息主要贡献Timestep ShrinkageEarly C
Jm18.6绘制量化步长变化时,码率和psnr的关系
jm下载地址为:http://iphome.hhi.de/suehring/tml/ 修改步长的参数为:QPISlice 、QPPSlice 、QPBSlice InputFile :输入的yuv文件 FrameRate:帧率 SourceWidth = 320 # Source frame width SourceHeight =
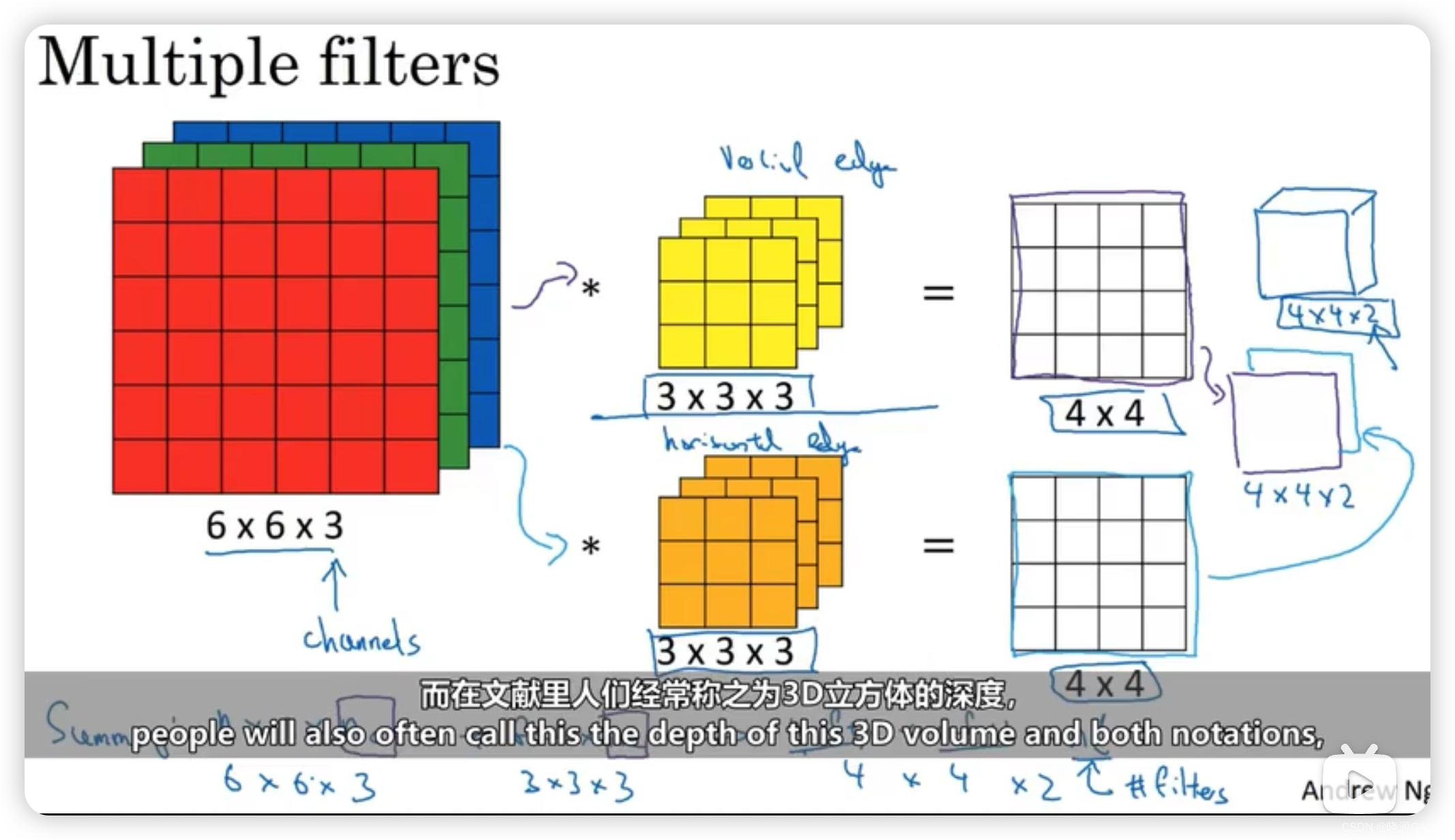
深度学习|10.5 卷积步长 10.6 三维卷积
文章目录 10.5 卷积步长10. 6 三维卷积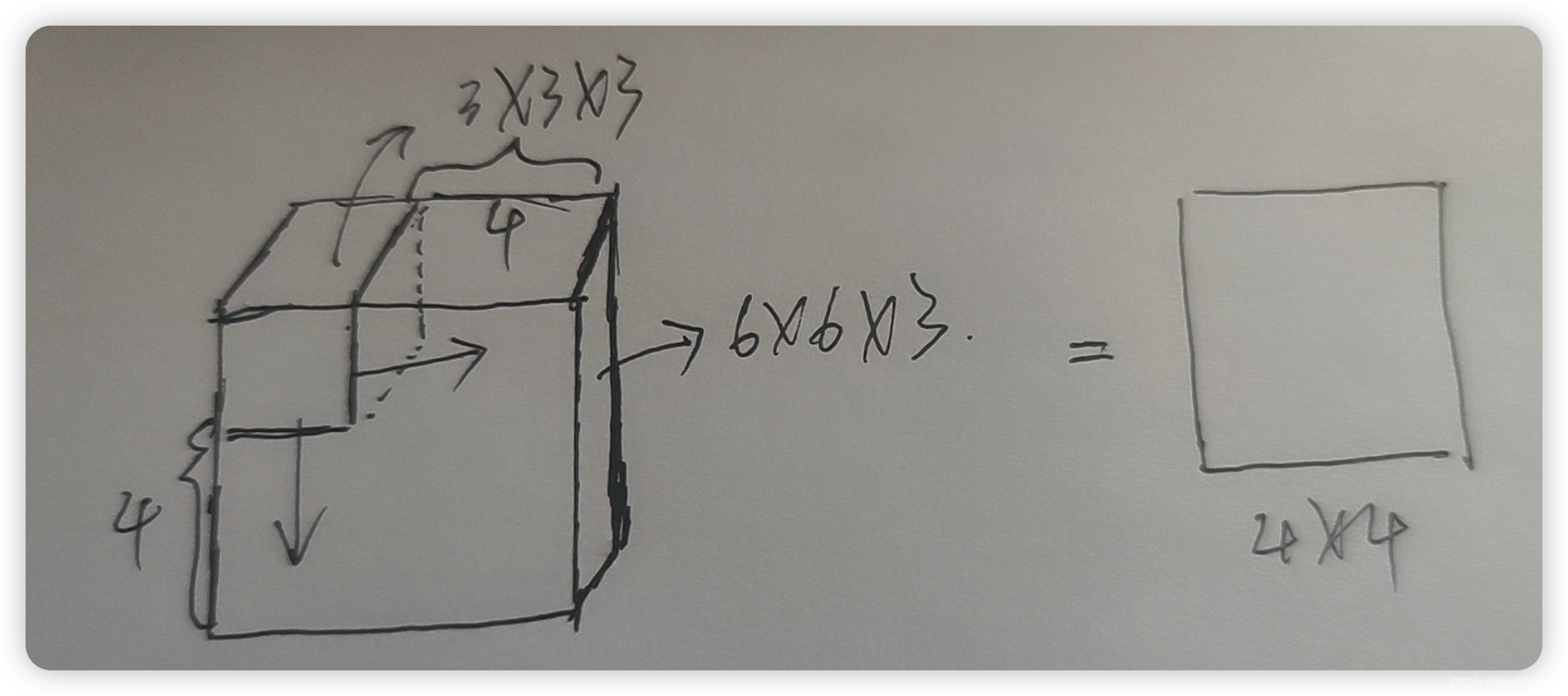 10.5 卷积步长 卷积步长是指每计算一次卷积,卷积移动的距离。 设步长为k,原矩阵规模为nxn,核矩阵规模为fxf,则k+k+k+k+…+k+f<n,新生成的
Excel实现字母+数字拖拉自动递增,步长可更改
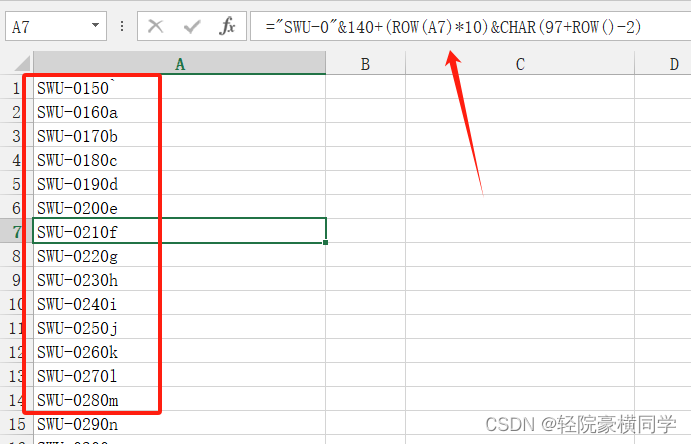
目录 1、带有字母的数字序列自增加(步长可变) 2、仅字母自增加 3、字母+数字同时自增 1、带有字母的数字序列自增加(步长可变) 使用Excel通常可以直接通过拖拉的方式,实现自增数字,但对于可变步长的自增,需要使用公式实现。 公式:="SWU-0"&(140+(ROW(A9)*10)) 公式说明: &表示连接各个字符;RO
梯度下降算法步长和收敛条件的设置的一些看法
在上一篇中介绍了梯度下降算法,还是利用了上面的那个x^2+y^2的例子,来求解下,代码如下: function [] = gradient(step, threadhold)%在这里主要是演示对z=x^2+y^2的用梯度下降算法%设置x和y的初始值%x = 100;y = 100;%先计算前两个步骤的值last_step_result = x*x + y*y;x = x - s
强化学习小笔记 —— 如何选择合适的更新步长
在强化学习中,动作价值函数的更新可以使用增量法,如下所示: Q k = 1 k ∑ i = 1 k r i = 1 k ( r k + ∑ i = 1 k − 1 r i ) = 1 k ( r k + ( k − 1 ) Q k − 1 ) = 1 k ( r k + k Q k − 1 − Q k − 1 ) = Q k − 1 + 1 k [ r k − Q k − 1 ] \begin{
GUI疑难杂症——GUI界面设置Simulink变步长值
问题简述:GUI界面中放置一个可编辑文本edit1,通过改变edit1值来控制Simulink模型的步长值,此处选择步长类型为变步长(Variable-step),需要设置的值为Max step size(变步长最大值)。 解决步骤: 在MATLAB命令行输入以下代码,查看名为Model_Name模型的所有属性: >>simget(‘Mode_Name’); %%此处Model_Name为自
H.264——量化参数QP和量化步长Qstep
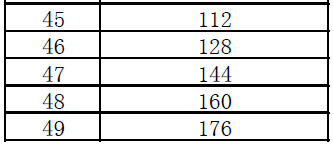
目录 什么是QP和QstepQP与Qsetp对应图QP的调节效果量化min qp 最小量化步长max qp最大量化步长 什么是QP和Qstep 量化参数QP是量化步长Qstep的序号。 对于亮度(Luma)编码而言,量化步长Qstep共有52个值,QP取值0-51对于色度(Chroma)编码,Q的取值0-39。 QP与Qsetp对应图 QP的调节效果 QP取最小
H.264量化参数QP和量化步长Qstep
1. 量化参数QP是量化步长Qstep的序号。对于亮度(Luma)编码而言,量化步长Qstep共有52个值,QP取值0~51,对于色度(Chroma)编码,Q的取值0~39。 QP取最小值0 时,表示量化最精细;相反,QP取最大值51时,表示量化是最粗糙的。 QP和Qstep具有线性相关性,Qstep随着QP的增加而增加,每当QP值增加6,Qstep便增加一倍。 量化是在
c语言最优步长坐标轮换法,无约束优化方法-直接方法(坐标轮换法)
无约束最优化方法的一般步骤可以总结如下: 选择初始点 ,这一点越靠近局部极小点 越好; 已取得某设计点 ,选择一个设计方向 ,沿此方向搜索,函数值需是下降的, 是下降方向; 从 出发,沿 方向进行搜索,确定步长因子 ,得到新的设计点 , 并满足
Kotlin中的步长
步长是 Kotlin 中用于迭代区间或集合时控制迭代步进的概念。在 Kotlin 中,我们可以使用 step 关键字来指定迭代时的步长。 在 Kotlin 中,有多种方式可以定义一个区间(Range)。我们将通过以下示例代码来展示不同类型的区间以及如何使用步长进行迭代: fun main() {// 正向区间 [1, 4]for (i in 1.rangeTo(4)) {print("$i\t
tqdm包进度条长度固定,前后缀步长配置,设置自定义显示内容
呆呆象呆呆的所有博客目录 1、tqdm包安装 pip install tqdm 2、引用 引用包的时候注意细节,不是直接引用,而是引用里面的一个类 from tqdm import tqdm或者from tqdm import trange 3、使用方法1:tpdm和trange最简单方法 主要方式1:使用tqdm 是使用tqdm封装任意迭代器 代码1演示如下(包装r