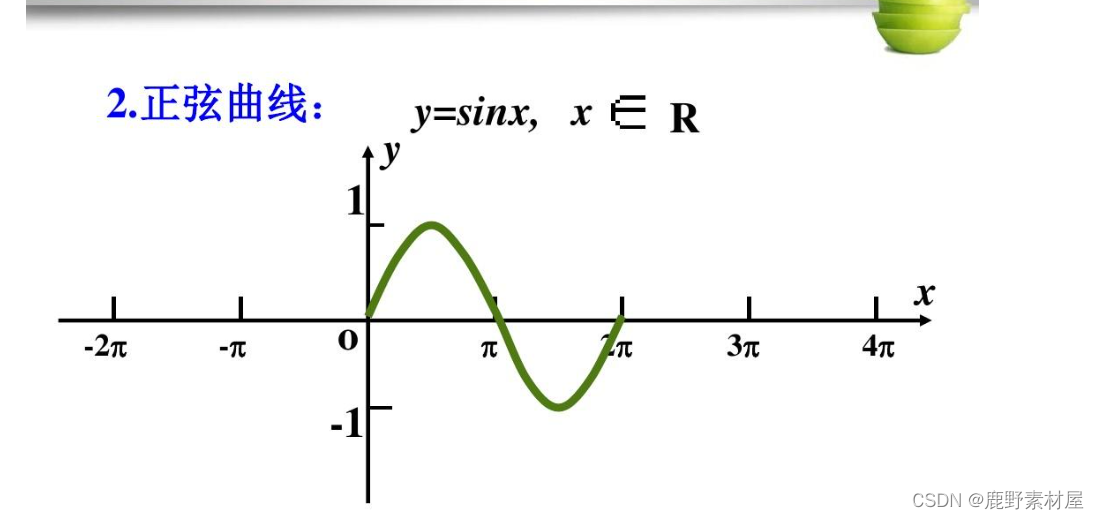
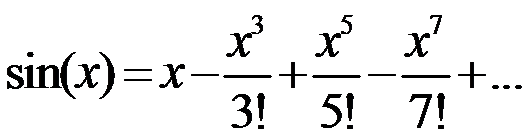正弦专题
基于自适应狮群算法优化GRU神经网络进水量预测,gsclst-gru进水量预测,基于黄金正弦改进的狮群算法优化GRU进水量预测
目录 背影 摘要 LSTM的基本定义 LSTM实现的步骤 gru的原理 狮群群算法原理 基于自适应狮群算法优化BILSTM神经网络进水量预测,gsclst-gru进水量预测,基于黄金正弦改进的狮群算法优化BILSTM进水量预测 结果分析 展望 参考论文 背影 传统的方法回归分析容易陷入局部最优准确率低,为提高精度,本文用 ,gsclst-gru进水量预测,基于黄金正弦改进的狮群算法优化GRU
Python优化算法17——黄金正弦算法(GSA)
科研里面优化算法都用的多,尤其是各种动物园里面的智能仿生优化算法,但是目前都是MATLAB的代码多,python几乎没有什么包,这次把优化算法系列的代码都从底层手写开始。 需要看以前的优化算法文章可以参考:Python优化算法_阡之尘埃的博客-CSDN博客 黄金正弦算法(Golden Sine Algorithm, GSA)是一种基于自然启发的优化算法,利用黄金比例和正弦函数的特性进
用正弦函数实现跳跃弧线
1,想法来源 在游戏中,需要实现一个跳跃的功能,我最开始用的是重力加速度。即水平速度不变,垂直速度加等于重力,但策划觉得不好调。 最后决定使用固定的曲线函数实现,即X轴速度不变,Y轴按照距离最高点的距离求位置。 这样就可以就联想到了正弦函数。 2,正弦函数 标准的正弦函数如下: 代码实现如下: double a = 30; // converting value to radi
仿真实例1——正弦函数仿真(ROM)
欲观原文,请君移步微信 对于FPGA来说,产生三角函数,幂函数,指数函数或者log函数等,如果真的使用乘法器来撘电路,那是极其消耗DSP资源的 ,所以一般情况下都是采用LUT进行查表获取的。 所以产生一个正弦波形的实现步骤如下:1.正弦函数的在给定取值范围内的函数值2.将正弦函数的函数值存入ROM或者RAM中(初始化)3.从ROM或者RAM中读出函数值 1.matlab获取正弦函数值 t=[
C语言实现正弦信号扫频
C语言实现正弦信号扫频 包含必要的头文件:首先,你需要包含 <stdio.h> 和 <math.h> 头文件,分别用于输入输出和数学函数的使用。 定义扫频参数:定义正弦扫频的参数,例如起始频率、结束频率、扫频时间等。 生成正弦波信号:使用正弦函数生成扫频信号,可以根据当前时间和扫频参数计算出对应的频率。 输出信号:将生成的正弦扫频信号输出到音频设备或保存为音频文件。 控制扫频过程:可以使
【优化算法】正弦余弦算法(SCA)【含Matlab源码 1308期】
⛄一、获取代码方式 获取代码方式1: 完整代码已上传我的资源:【优化算法】正弦余弦算法(SCA)【含Matlab源码 1308期】 点击上面蓝色字体,直接付费下载,即可。 获取代码方式2: 付费专栏Matlab优化求解(初级版) 备注: 点击上面蓝色字体付费专栏Matlab优化求解(初级版),扫描上面二维码,付费29.9元订阅海神之光博客付费专栏Matlab优化求解(初级版),凭支付凭证,私
通用MCU使用查表计算正弦值sin和查看计算时间
生成SIN_COS_TABLE 四分之一周期为256个点 #include <stdio.h>#include <math.h>#define POINT_NUM 256#define PI 3.141592fint main(){for (int i = 0; i < POINT_NUM; i++) {printf("[ %d:\t0x%04X ]", i, (un
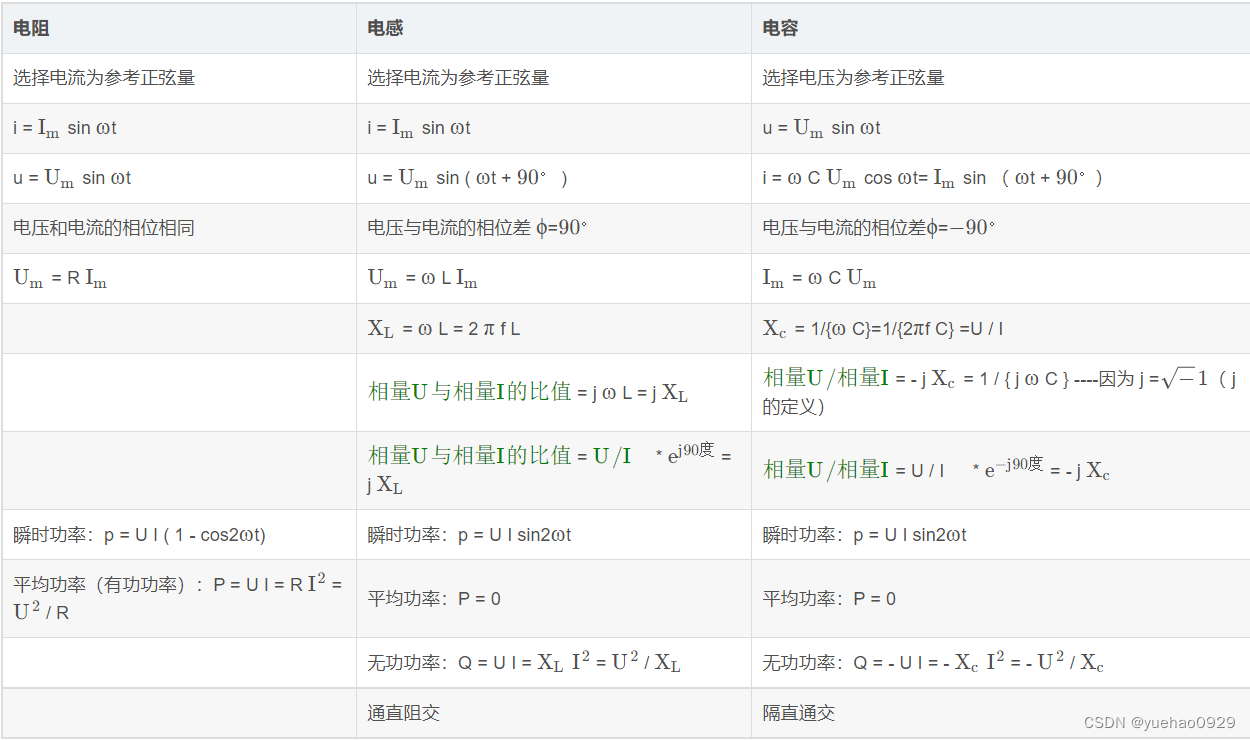
电工技术学习笔记——正弦交流电路
一、正弦交流电路 1. 正弦量的向量表示法 向量表示方法:正弦交流电路中,相量表示法是一种常用的方法,用于描述电压、电流及其相位关系。相量表示法将正弦交流信号表示为复数,通过复数的运算来描述电路中各种参数的相互关系 2.向量表示法的计算步骤 确定电压、电流的幅值和相位:根据实际电路情况,确定电压、
正弦实时数据库(SinRTDB)的使用(8)-过滤查询
前文已经将正弦实时数据库的使用进行了介绍,需要了解的可以先看下面的博客: 正弦实时数据库(SinRTDB)的安装 正弦实时数据库(SinRTDB)的使用(1)-使用数据发生器写入数据 正弦实时数据库(SinRTDB)的使用(2)-接入OPC DA的数据 正弦实时数据库(SinRTDB)的使用(3)-用户管理 正弦实时数据库(SinRTDB)的试用(4)-快照查询 正弦实时数据库(Sin
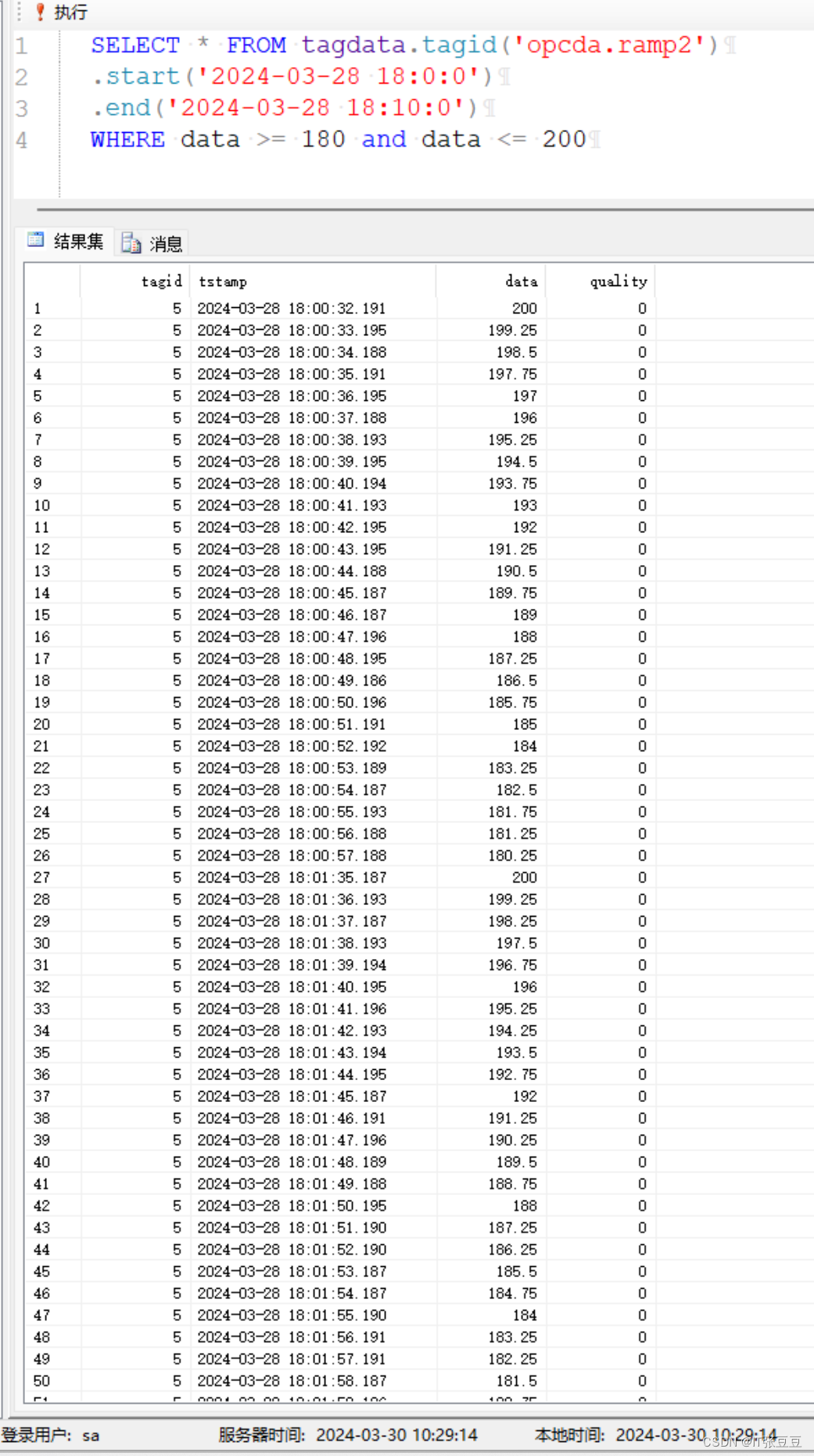
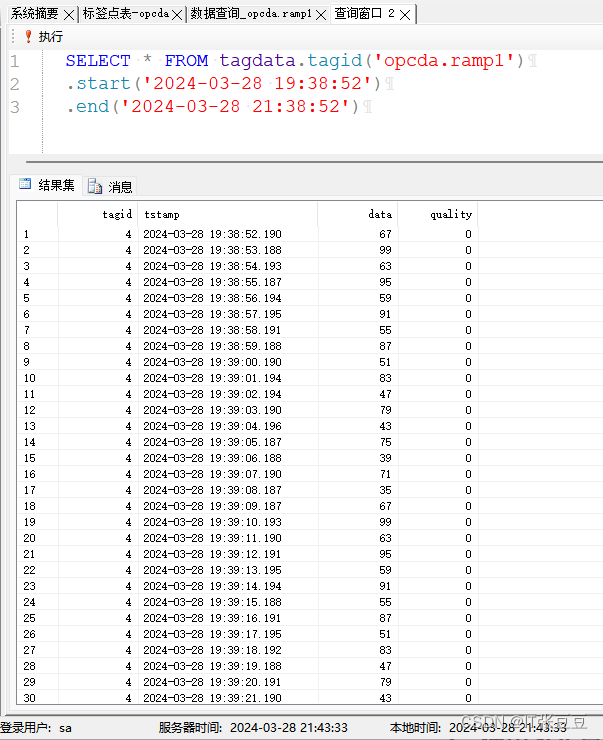
正弦实时数据库(SinRTDB)的使用(5)-历史数据查询
前文已经将正弦实时数据库的使用进行了介绍,需要了解的可以先看下面的博客: 正弦实时数据库(SinRTDB)的安装 正弦实时数据库(SinRTDB)的使用(1)-使用数据发生器写入数据 正弦实时数据库(SinRTDB)的使用(2)-接入OPC DA的数据 正弦实时数据库(SinRTDB)的使用(3)-用户管理 正弦实时数据库(SinRTDB)的试用(4)-快照查询 若需要试用正弦实时数据
正弦实时数据库(SinRTDB)的使用(5)-历史数据查询(一)
前文已经将正弦实时数据库的使用进行了介绍,需要了解的可以先看下面的博客: 正弦实时数据库(SinRTDB)的安装 正弦实时数据库(SinRTDB)的使用(1)-使用数据发生器写入数据 正弦实时数据库(SinRTDB)的使用(2)-接入OPC DA的数据 正弦实时数据库(SinRTDB)的使用(3)-用户管理 正弦实时数据库(SinRTDB)的试用(4)-快照查询 若需要试用正弦实时数据
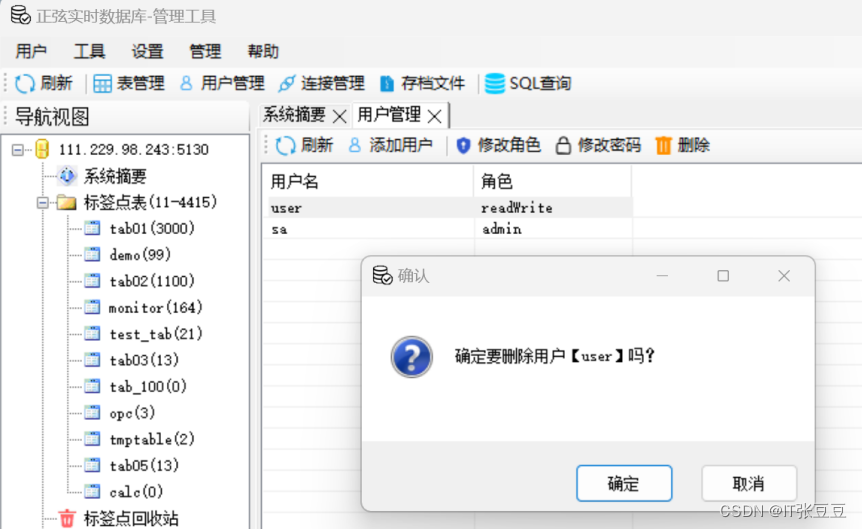
正弦实时数据库(SinRTDB)使用(3)-用户管理
通过实时数据库管理工具登录后,在头部功能区的用户管理或左侧导航菜单的用户管理都可以打开用户管理功能界面,用户管理功能界面展示在中部主窗口区。 用户管理界面如下所示: 用户管理顶部包含刷新、添加用户、修改角色、修改密码及删除用户等功能; 用户管理界面包含展示所有用户信息列表,包含用户名及角色信息。角色包含如下几种: admin: 管理员,若用户名为sa,则
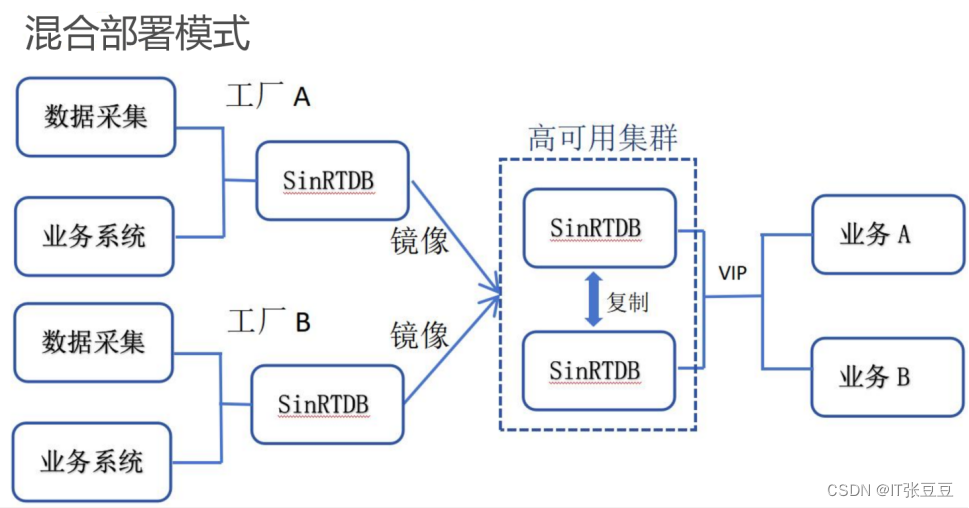
正弦实时数据库(SinRTDB)的部署架构
为了适应各种类型的项目需求,正弦实时数据库支持单机部署、双主高可用集群部署、混合部署模式,各部署模式的特点如下: 单机部署 应用于风力发电、光伏、火电 等厂、站级监控系统。支持组态、实时计算、报警服务、报表统计等业务。 双主高可用集群部署 应对高可用场景下的风力发电、光伏、火电 等厂、站级监控系统。支持组态、实时计算、报警服务、报表统计等业务。两台数据库服务可以同时对外提供服务,提高数
电力电子论文中的正弦激励响应公式推导
论文推导计划 数学原理(正弦激励下的响应计算) 参考书:高等数学、工程数学、自动控制原理、电路原理 上一期(二阶微分方程求解) 二阶线性微分方程求解链接: 二阶线性微分方程求解 文章目录 论文推导计划前言一、基本的数学原理电路理论中的 L a p l a c e Laplace Laplace变换理论(暂态解+稳态解)相量法(只可求稳态解) 二、具体应用1.一阶RC电路的正弦激励 总结
c语言实验--正弦,C语言实验报告-正弦信号模拟采样及特征参数分析软件设计
南昌航空大学实验报告 2012 年 12 月 13 日 课程名称: C语言实验 实验名称:正弦信号模拟采样及特征参数分析软件设计 班级: xxxxx班 xx号 姓名: XXX 地点: 指导教师评定: 签名: 一、实验目的 1. 了解正弦信号采样的基本原理; 2. 了解正弦信号采样的离散处理方法; 3. 进一步掌握C语言输入输出语句的使用和编程方法; 4. 进一步掌握C语言顺序结构、选择结构和循环
c语言实验--正弦,c语言实验报告-正弦信号模拟采样及特征参数分析软件设计.doc...
c语言实验报告-正弦信号模拟采样及特征参数分析软件设计.doc 南昌航空大学实验报告2012年12月13日课程名称:C语言实验实验名称:正弦信号模拟采样及特征参数分析软件设计班级:xxxxx班xx号姓名:XXX地点:指导教师评定:签名:一、实验目的1.了解正弦信号采样的基本原理;2.了解正弦信号采样的离散处理方法;3.进一步掌握C语言输入输出语句的使用和编程方法;4.进一步掌握C语言顺序结构、
【信号分析与处理】matlab图像法验证正弦信号的两个性质
1.同频率正弦型信号相加结果仍是同频率正弦信号(由辅助角公式) 2.如果一个正弦信号的频率f1是另外一个正弦信号f0的整数倍,则合成信号是频率为f0的非正弦信号 x=[-10:0.01:10];>> y1=sin(x);>> y2=sin(2*x);>> y3=cos(x+pi/6);>> plot(x,y1+y3);>>> plot(x,y1+y2); 得到的图像结果如下: 同
连续正弦信号使用FFT做频谱分析
一个偶对称的连续波,如何用FFT做频谱分析,用正弦信号做了个例子,不论任何连续信号,都可以仿照这个例子进行频谱分析。 %==========================================================================%Name: sinfft.m%Desc: 使用FFT求y=sin(2*pi*10*t)的频谱,抽样频率为40hz(大于信号最高频
为什么信号都能够用正弦信号表示?
1 矢量分解 我们知道两个矢量 V 2 → a n d V 1 → 相互正交,夹角为 90 ° 我们知道两个矢量\overrightarrow{V_2}and\overrightarrow{V_1}相互正交,夹角为90\degree 我们知道两个矢量V2 andV1 相互正交,夹角为90° 即 V 2 → ⋅ V 1 → = ∣ V 1 ∣ ⋅ ∣ V 2 ∣ c o s 9
51控制ST7735画正弦函数
主控芯片:STC8A8KS4A12 显示屏参数:1.8寸 128X160像素彩屏 ST7735驱动芯片 一共三个文件:main.C ST7735.C ST7735.H 如有疑惑发邮件至3456939016@QQ.COM,本人也是小白,欢迎打扰 如图,代码在图片后: main.C#include <STC8.H>#include <math.h>#include "
zzuli:1053正弦函数
题目描述 输入x,计算上面公式的前10项和。 输入 输入一个实数x。 输出 输出一个实数,即数列的前10项和,结果保留3位小数。 样例输入 Copy 1 样例输出 Copy 0.841 #include <stdio.h>int main(){int i;double x;scanf("%lf",&x);double sum=0,den=1,mol=x,sign=1
1.5C语言 双曲正弦函数(*) 优化麦克劳林公式
一.传统算法 #include<stdio.h>#include<math.h>int jc(int x);int main(){double x,eps,y=0.0;scanf("%lf%lf",&x,&eps);int de=1,i=1;double item=1.0;while(fabs(item)>=eps){item=pow(x,i)/jc(de);i+=2;y+=item;
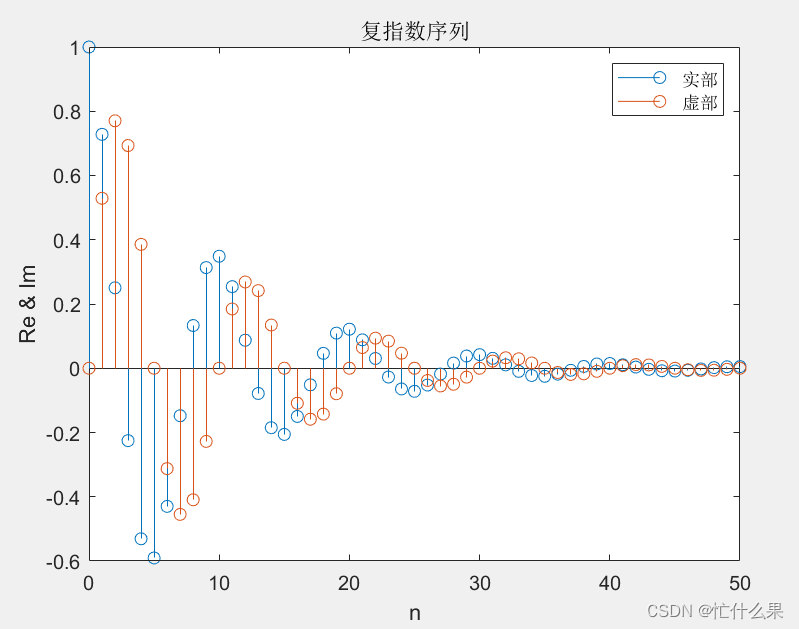
用 MATLAB 产生单位抽样序列、单位阶跃序列、矩形序列、正弦序列和复指数序列
%% 单位抽样(脉冲)序列(冲激函数)% 参数设置n = -10:10; % 定义时间范围delta = (n == 0); % 生成单位抽样序列% 绘图figure;stem(n, delta);title('单位抽样序列');xlabel('n');ylabel('delta[n]');%% 单位阶跃序列% 参数设置n = -10:10; % 定义时间范围u = (n >
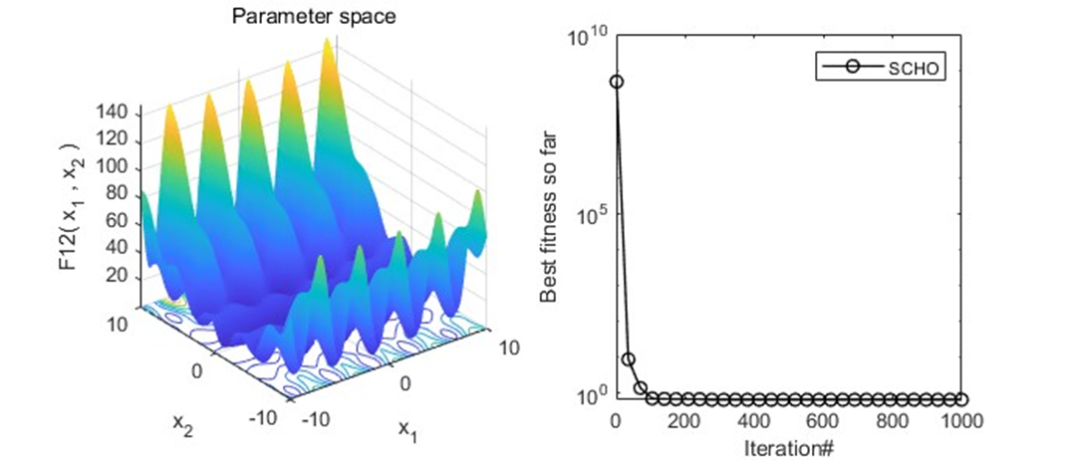
2023年智能算法之双曲正弦余弦优化器(SCHO),原理公式详解,附matlab代码
双曲正弦余弦优化器(Sinh Cosh Optimizer,SCHO)是一种新型元启发式算法,该算法基于双曲正弦和双曲余弦特性的数学启发,具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2023年10月发表在SCI一区,Top顶刊Knowledge-Based Systems上。 SCHO的灵感来源有三点。首先,如何在勘探和开发之间取得平衡是一个巨大的挑战,其次,面对复杂多样的问题,仍需
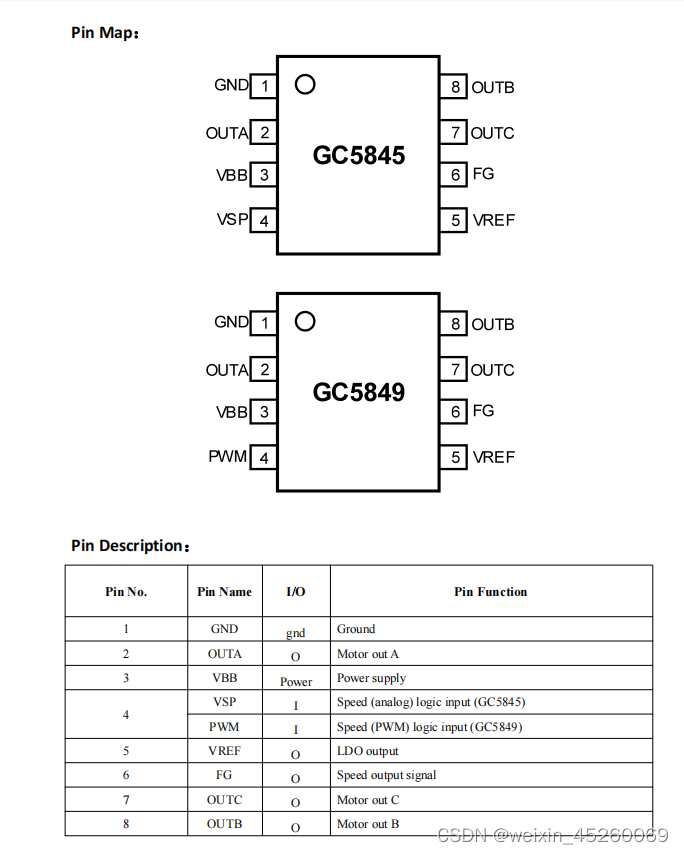
三相电机驱动器纳入正弦驱动芯片GC5845和GC5849,180°正弦驱动,低噪音高效控制算法支持
GC5845和GC5849是一个三相电机驱动器纳入正弦驱动器,以尽量减少中等功率风扇的噪音和振动。提供速度输入以控制电机速度。这允许通过消除外部可变电源节省系统成本。或者,可以使用低至4V的电源调制来调节电机速度。 芯片的特点: 180°正弦驱动,低噪音高效控制算法支持 无传感器操作 模拟速度输入(GC5845)