为什么信号都能够用正弦信号表示？

1 矢量分解

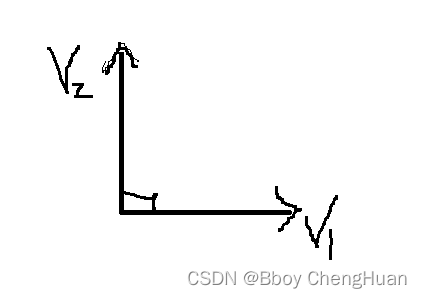
$$我们知道两个矢量\overrightarrow{V_2}and\overrightarrow{V_1}相互正交，夹角为90°$$
即$$\overrightarrow{V_2}\cdot \overrightarrow{V_1}=\left|V_1\right|\cdot \left|V_2\right|cos90°=0$$
在这个平面坐标上可以对任意方向的信号进行二维分解

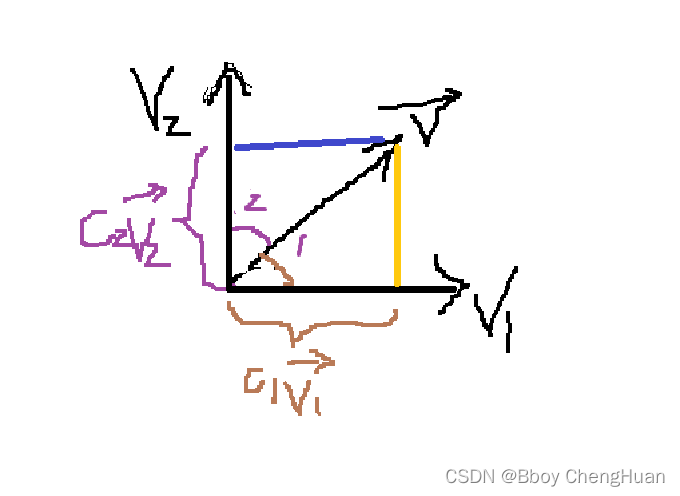
如上图我们对V进行分解即使用V1和V2表示出来
$$\overrightarrow{V}=c_1{\overrightarrow{V}}_2+c_2{\overrightarrow{V}}_2$$
其中$$c_1=\frac{\left|\overrightarrow{V}\right|cos{\theta }_1}{\left|{\overrightarrow{V}}_1\right|}=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_1}{{\overrightarrow{V}}_1\cdot {\overrightarrow{V}}_1}$$
$$c_2=\frac{\left|\overrightarrow{V}\right|cos{\theta }_2}{\left|{\overrightarrow{V}}_2\right|}=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_2}{{\overrightarrow{V}}_2\cdot {\overrightarrow{V}}_2}$$
同理我们对于三维向量进行分解

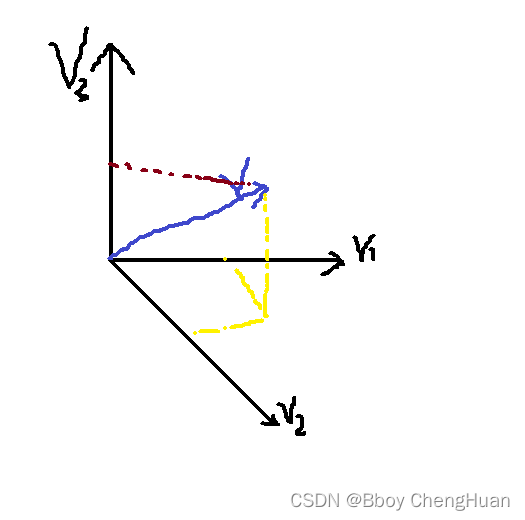
$$\overrightarrow{V}=c_1{\overrightarrow{V}}_2+c_2{\overrightarrow{V}}_2+c_3{\overrightarrow{V}}_3$$
其中$$c_1=\frac{\left|\overrightarrow{V}\right|cos{\theta }_1}{\left|{\overrightarrow{V}}_1\right|}=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_1}{{\overrightarrow{V}}_1\cdot {\overrightarrow{V}}_1}$$
$$c_2=\frac{\left|\overrightarrow{V}\right|cos{\theta }_2}{\left|{\overrightarrow{V}}_2\right|}=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_2}{{\overrightarrow{V}}_2\cdot {\overrightarrow{V}}_2}$$
$$c_3=\frac{\left|\overrightarrow{V}\right|cos{\theta }_3}{\left|{\overrightarrow{V}}_3\right|}=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_3}{{\overrightarrow{V}}_3\cdot {\overrightarrow{V}}_3}$$
由低维推广至高维，我们可以知道n维空间的任意矢量V,可以准确表示为n个正交矢量的线性组合，即：
$$\overrightarrow{V}=c_1{\overrightarrow{V}}_2+c_2{\overrightarrow{V}}_2+\cdots +c_n{\overrightarrow{V}}_n$$
其中任意$$c_r=\frac{\overrightarrow{V}\cdot {\overrightarrow{V}}_r}{{\overrightarrow{V}}_r\cdot {\overrightarrow{V}}_r}$$
$${\overrightarrow{V}}_i\cdot {\overrightarrow{V}}_j=0(i\ne j)$$

我们可以将这种矢量分解的思想推广至信号分解中。

2 信号分解

信号正交：在($t_1$,$t_2$)区间的两个函数${\phi }_1（t）$和${\phi }_2（t）$满足${\int }_{t_1}^{t_2}{\phi }_1（t）{\phi }_2（t{）}^{\ast }\mathrm{d}t=0$（信号卷积为0），则称${\phi }_1（t）$和${\phi }_2（t）$在该区间内正交。
对于已知信号的分解我们需要先找到一个正交函数集（即映射的平面坐标轴，于多个函数而言在($t_1$,$t_2$)区间的n个函数${\phi }_1（t），{\phi }_2（t），\cdots ,{\phi }_n（t）$满足${\int }_{t_1}^{t_2}{\phi }_i（t）{\phi }_j（t{）}^{\ast }\mathrm{d}t=0（i\ne j）$，则称该函数集在该区间内正交。

另外信号的分解更加苛刻一点，需要完备正交函数集即在正交函数集外，不存在任何函数$\phi (t)$满足
${\int }_{t_1}^{t_2}\phi （t）{\phi }_j（t{）}^{\ast }\mathrm{d}t=0（{\phi }_j取自正交函数集）$

则该正交函数集便升级为完备正交函数集

恰好有两个典型的完备正交函数集在区间$(t_0,t_0+T)$
(1)三角函数集{$1，cos(n\Omega t),sin(n\Omega t),n=1,2,\cdots$}
(2)虚指数函数集{$e^{jn\Omega t},n=0,\pm 1,\pm 2,\cdots$}
可自行进行证明，傅里叶已证实
接下来我梦使用信号正交分解

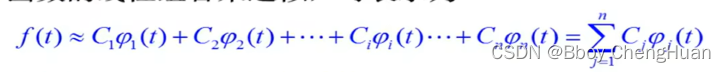
为了求解$f(t)$与我们近似函数之间误差最小，引入一个均方误差函数
$$\overline{{\epsilon }^2}=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}[f(t)-\sum _{j=1}^n{C}_j{\phi }_j(t){]}^2\mathrm{d}t$$
对其求$C_i$偏导,并令其等于0
$$\frac{\partial \overline{{\epsilon }^2}}{\partial C_i}=\frac{\partial {\int }_{t_1}^{t_2}[f(t)-{\sum }_{j=1}^n{C}_j{\phi }_j(t){]}^2\mathrm{d}t}{\partial C_i}$$
对于求和项而言两两正交所以只留下$C_i^2{\phi }_i^2$，展开被积积分，并求导，只有两项不为0即
$$-2{\int }_{t_1}^{t_2}f(t){\phi }_i(t)\mathrm{d}t+2C_i{\int }_{t_1}^{t_2}{\phi }_i^2(t)\mathrm{d}t=0$$
即
$$C_i=\frac{{\int }_{t_1}^{t_2}f(t){\phi }_i(t)\mathrm{d}t}{{\int }_{t_1}^{t_2}{\phi }_i^2(t)\mathrm{d}t}=\frac{1}{K}{\int }_{t_1}^{t_2}f(t){\phi }_i(t)\mathrm{d}t$$
回代：

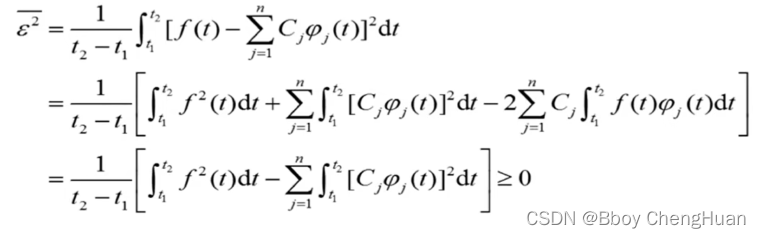
可知取得项数越多即n越大，均方误差越小。当$n\to \infty$时，均方误差为0

3 结论

任意信号可以表示为无穷个正交函数之和即：
$$f(t)=C_1{\phi }_1（t）+C_2{\phi }_2（t）+\cdots +C_n{\phi }_n（t）=\sum _{i=1}^{\infty }{C}_i\phi (t)$$
也可称为正交展开式，或者广义傅里叶级数。
因此任意信号可以使用正弦完备正交函数集来表示

参考视频讲解：

郭宝龙信号系统讲解