2023年智能算法之双曲正弦余弦优化器（SCHO），原理公式详解，附matlab代码

双曲正弦余弦优化器（Sinh Cosh Optimizer，SCHO）是一种新型元启发式算法，该算法基于双曲正弦和双曲余弦特性的数学启发，具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2023年10月发表在SCI一区，Top顶刊Knowledge-Based Systems上。

SCHO的灵感来源有三点。首先，如何在勘探和开发之间取得平衡是一个巨大的挑战，其次，面对复杂多样的问题，仍需要提出新的元启发式算法。最后，基于数学启发的优化算法的提出，如sin、cos算法和算术优化算法(AOA)，为研究元启发式算法指明了一个新的可能方向。双曲函数是三角函数中常见的一类，其中sinh和cosh是最基本的双曲函数。元启发式算法可以利用cosh和sinh的两个特性。一是cosh值总是大于1，这是勘探与开发的关键边界，另一种是sinh值在[−1,1]区间内，且接近于零，可以提高勘探开发效率。

算法原理

（1）初始化阶段

与其他元启发式算法一样，SCHO也从随机初始化一组候选解开始。初始化的候选解的数学公式如下所示：  其中X是由以下公式得到的随机候选解集合，  表示第i个解的第j个位置，N表示候选解的个数，dim为问题维数。  其中rand表示[0,1]中的随机值，ub和lb分别为变量的上界和下界。

（2）勘探阶段

在本研究中，探索下一个位置仍然与它的位置有关，并得到了迄今为止的最优解。在优化过程中，探索分为两个阶段，应该存在于以后的迭代中，以逃避局部最优。在这两个阶段之间切换的值通过以下数学公式：  其中Max迭代表示迭代的最大值，floor是MATLAB中向下舍入的函数，ct是用于设置两相切换点的系数。在第一阶段中，在早期的迭代中，搜索代理位置附近的搜索空间外部将被探索，然后搜索代理将逐渐接近获得的最佳解。第一阶段勘探位置更新函数的数学公式如下所示：  其中t表示当前迭代，  、  分别表示第i个解在当前迭代和下次迭代中的第j个位置；  为到目前为止得到的最优解的第j个位置，r1,r2为区间[0,1]内的随机数；  为第一勘探阶段  的权重系数，控制第一阶段候选解远离自身，逐渐向最优解探索，通过以下公式计算得到。  其中  为单调递减函数，由以下公式计算，  和  为[0,1]中的随机数；  是控制第一阶段勘探精度的敏感系数，固定为0.388；  从一个很小的值逐渐减小，这说明了自身位置对于位置更新的重要性，因此，候选解在第一阶段逐渐远离自己，然后寻找最优解。其中  为控制勘探精度的敏感系数，根据本案例实验，其值为0.45。  在第二阶段的探索中，搜索代理几乎不受最佳解的影响，因此它们基于当前位置进行无方向性的探索。其位置更新函数的数学公式如下所示：  其中，ε是一个极小的正数，根据本文实验，ε为0.003。W2为第二勘探阶段最佳的  的权重系数，  乘以ε大大削弱了最优解对当前解的影响，从而导致对  周围的候选解进行无向随机勘探，W2由以下公式计算得到：  其中r6为[0,1]中的随机数，a2为用以下公式计算得到的单谐递减函数：  式中，n为控制第二阶段勘探精度的敏感系数，根据本文实验，取值为0.5。

（3）开发阶段

为了充分利用搜索空间，开发分为两个阶段，在整个迭代过程中进行。在第一个开发阶段，开发了X的邻近空间，因此开发公式如下表示：  其中  ,  属于区间[0，1]中的随机数。  是第一阶段开发的权重系数，它控制候选解从近到远地开发其周围的搜索空间，其数学公式如下所示： 其中  ,  是[0,1]中的随机数，a1已由上面公式定义，u与第一勘探阶段相同，固定为0.388。

在开发的第二阶段，候选解将围绕迄今为止获得的最优解进行深度开发，并且围绕最优解的开发强度将随着迭代次数的增加而增加。位置更新函数如下所示：  其中  、  是区间[0，1]中的随机数，  控制第二开发阶段的程度，它的绝对值在后面的迭代中逐渐增加，增加了开发程度。方程中绝对值前面的系数用于保持候选解的多样性。

（4）有界搜索策略

为了充分利用潜在的搜索空间，在SCHO中采用了一种类似于后期动物狩猎的策略，称为有界搜索策略。通过在早期迭代中探索整个搜索区域，可以找到潜在的搜索空间。为了充分挖掘和利用潜力空间，首先将所有候选解随机初始化到该潜力空间中，然后对该空间进行深度挖掘和利用。该策略的每一开始都是通过以下公式计算：  其中k是从1开始的正整数，  由以下公式计算，  分别表示开始当前和下一个有界搜索策略的迭代次数。α是一个敏感系数，它控制着潜空间深部勘探开发的精度，本实验通过实验将α取为4.6。  其中β控制启动有界搜索策略的值，并设置为1.55。当SCHO每次都使用有界搜索策略时，优化问题的上界和下界将使用以下公式计算： 

其中  和  表示潜在搜索空间的上界和下界，  表示次优解的第  个位置。

 结果展示

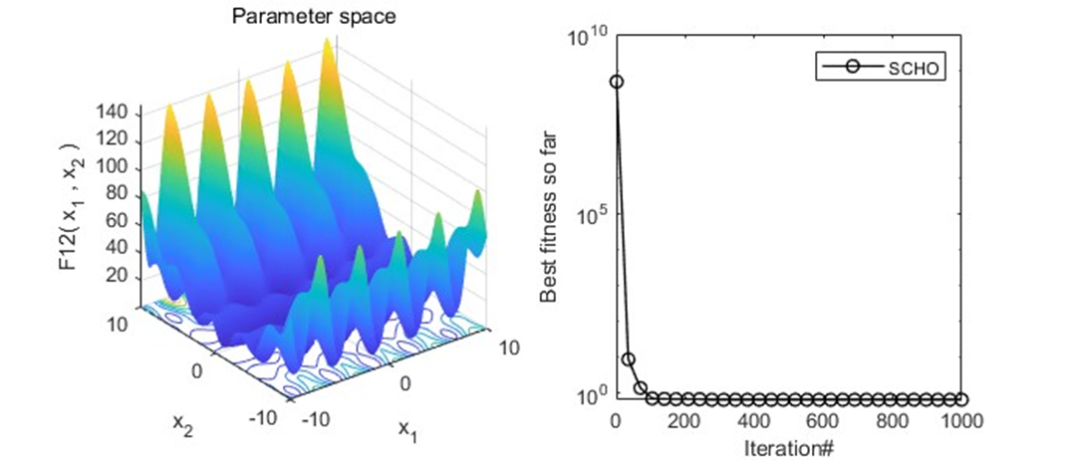
以为CEC2005函数集为例，进行结果展示：

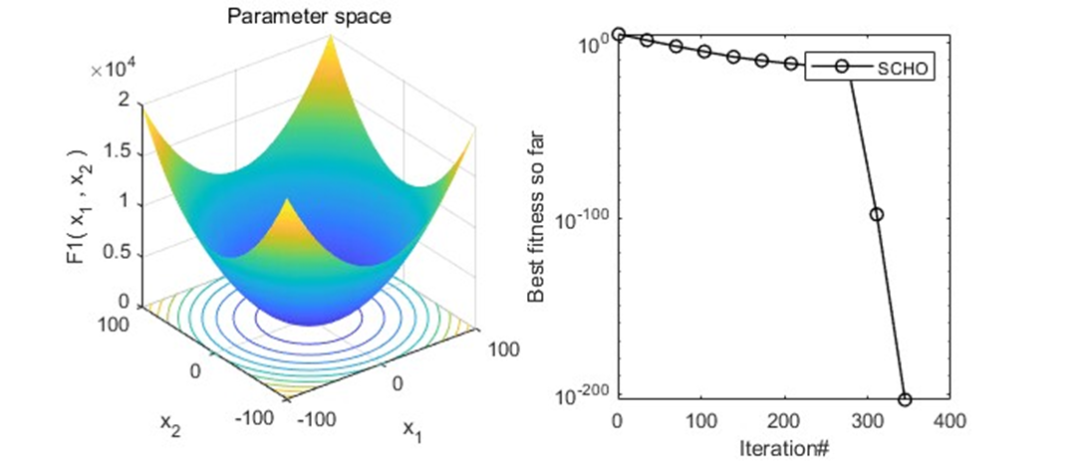
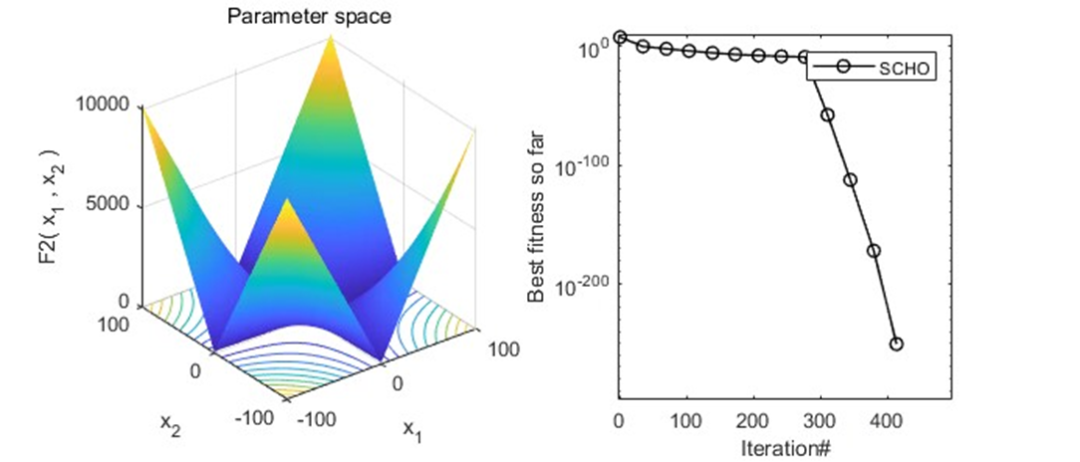
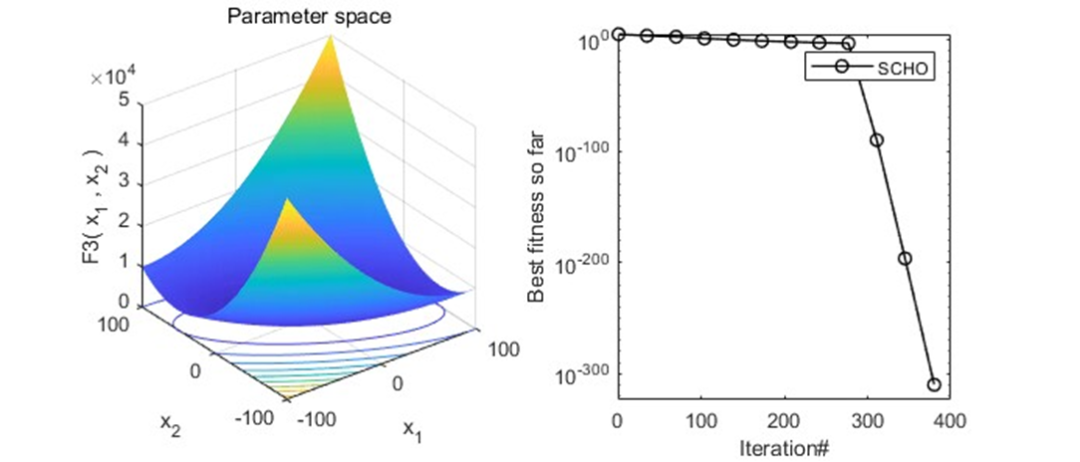
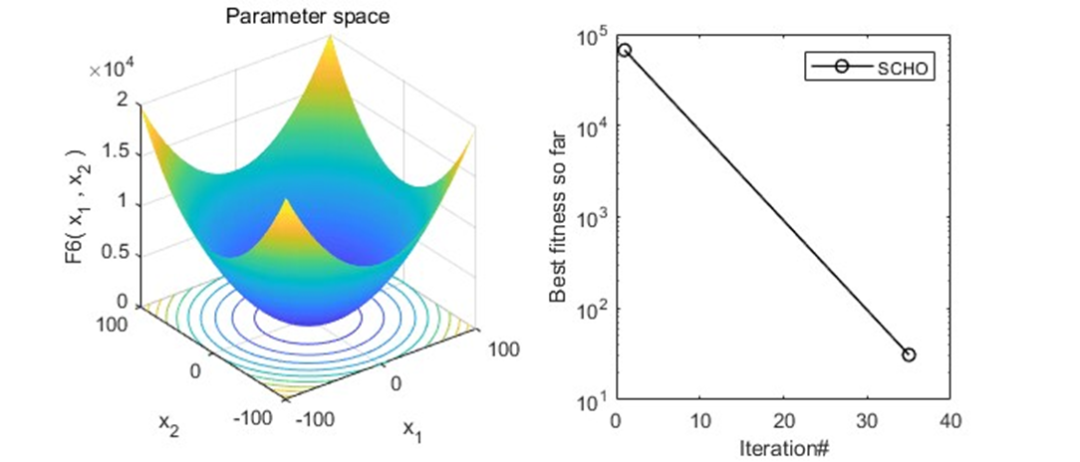
 MATLAB核心代码

function [Destination_fitness,Destination_position,Convergence_curve]=SCHO(N,Max_iteration,lb,ub,dim,fobj)Destination_position=zeros(1,dim);
Destination_fitness=inf;
Destination_position_second=zeros(1,dim);
Convergence_curve=zeros(1,Max_iteration);
Position_sort = zeros(N,dim);
%Initialize SCHO parameters
u=0.388;
m=0.45;
n=0.5;
p=10;
q=9;
Alpha=4.6;
Beta=1.55;
BS=floor(Max_iteration/Beta);
ct=3.6;
T=floor(Max_iteration/ct);
BSi=0;
BSi_temp=0;
ub_2=ub;
lb_2=lb;
%Initialize the set of random solutions
X=initialization(N,dim,ub,lb);
Objective_values = zeros(1,size(X,1));
% Calculate the fitness of the first set and find the best one
for i=1:size(X,1)Objective_values(1,i)=fobj(X(i,:));if Objective_values(1,i)<Destination_fitnessDestination_position=X(i,:);Destination_fitness=Objective_values(1,i);end
end
Convergence_curve(1)=Destination_fitness;
t=2; 
%Main loop
while t<=Max_iteration    for i=1:size(X,1) % in i-th solutionfor j=1:size(X,2) % in j-th dimension%update A by using Eq. (17)cosh2=(exp(t/Max_iteration)+exp(-t/Max_iteration))/2;sinh2=(exp(t/Max_iteration)-exp(-t/Max_iteration))/2;r1=rand();A=(p-q*(t/Max_iteration)^(cosh2/(sinh2)))*r1; % enter the bounded search strategyif t==BSi
ub_2=Destination_position(j)+(1-t/Max_iteration)*abs(Destination_position(j)-Destination_position_second(j));
lb_2=Destination_position(j)-(1-t/Max_iteration)*abs(Destination_position(j)-Destination_position_second(j));if ub_2>ubub_2=ub;endif lb_2<lblb_2=lb;endX=initialization(N,dim,ub_2,lb_2);                BSi_temp=BSi;BSi=0;end% the first phase of exploration and exploitation    if t<=T%3.6-3.62  r2=rand();r3=rand();a1=3*(-1.3*t/Max_iteration+m);r4=rand();r5=rand();if A>1sinh=(exp(r3)-exp(-r3))/2;cosh=(exp(r3)+exp(-r3))/2;W1=r2*a1*(cosh+u*sinh-1);if r5<=0.5X(i,j)=Destination_position(j)+r4*W1*X(i,j);elseX(i,j)=Destination_position(j)-r4*W1*X(i,j);  end                elsesinh=(exp(r3)-exp(-r3))/2;cosh=(exp(r3)+exp(-r3))/2;W3=r2*a1*(cosh+u*sinh);if r5<=0.5X(i,j)=Destination_position(j)+r4*W3*X(i,j);elseX(i,j)=Destination_position(j)-r4*W3*X(i,j);  endendelse% the second phase of exploration and exploitationr2=rand();r3=rand();a2=2*(-t/Max_iteration+n);W2=r2*a2;r4=rand();r5=rand();if A<1sinh=(exp(r3)-exp(-r3))/2;cosh=(exp(r3)+exp(-r3))/2;X(i,j)= X(i,j)+(r5*sinh/cosh*abs(W2*Destination_position(j)-X(i,j)));elseif r4<=0.5X(i,j)=X(i,j)+(abs(0.003*W2*Destination_position(j)-X(i,j)));elseX(i,j)=X(i,j)+(-abs(0.003*W2*Destination_position(j)-X(i,j)));  endend endendBSi=BSi_temp;endfor i=1:size(X,1)         % Check if solutions go outside the search spaceand bring them backFlag4ub=X(i,:)>ub_2;Flag4lb=X(i,:)<lb_2;X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+(ub_2+lb_2)/2.*Flag4ub+lb_2.*Flag4lb;        % Calculate the objective valuesObjective_values(1,i)=fobj(X(i,:));
%         % Update the destination if there is a better solutionif Objective_values(1,i)<Destination_fitnessDestination_position=X(i,:);Destination_fitness=Objective_values(1,i);endend%find the second solutionif t==BSBSi=BS+1;BS=BS+floor((Max_iteration-BS)/Alpha);temp = zeros(1,dim);temp2 = zeros(N,dim);%sortingfor i=1:(size(X,1)-1)for j=1:(size(X,1)-1-i)if Objective_values(1,j) > Objective_values(1,j+1)temp(1,j) = Objective_values(1,j);Objective_values(1,j) = Objective_values(1,j+1);Objective_values(1,j+1) = temp(1,j);temp2(j,:) = Position_sort(j,:);Position_sort(j,:) = Position_sort(j+1,:);Position_sort(j+1,:) = temp2(j,:);   endendendDestination_position_second=Position_sort(2,:);%the second solutionendConvergence_curve(t)=Destination_fitness;t=t+1;
end

参考文献

[1]  Bai J, Li Y, Zheng M, et al. A sinh cosh optimizer[J]. Knowledge-Based Systems, 2023, 282: 111081.

完整代码获取方式：后台回复关键字：

TGDM101