双曲专题
NumPy 双曲函数与集合操作详解
NumPy 双曲函数 NumPy 提供了 sinh()、cosh() 和 tanh() 等 ufunc,它们接受弧度值并生成相应的双曲正弦、双曲余弦和双曲正切值。 示例: import numpy as npx = np.sinh(np.pi/2)print(x) 示例 找到数组 arr 中所有值的双曲余弦值: import numpy as nparr = np.array([np
偏微分方程算法之二阶双曲型方程交替方向隐格式
目录 一、研究目标 二、理论推导 2.1 显差分格式 2.2 交替方向隐格式 三、算例实现 四、结论 一、研究目标 本节的研究对象为如下的双曲型偏微分方程初边值问题: 为了保证连续性,公式(1)中相关函数满足: 二、理论推导 2.1 显差分格式 第一步:网格剖分。在三维长方体空间(二维平面加一维时间轴)进行网格
偏微分方程算法之二阶双曲型方程紧差分方法
目录 一、研究目标 二、理论推导 三、算例实现 一、研究目标 前面我们已经介绍了二阶双曲型方程显式、隐式差分格式,可否像抛物型方程一样,构建更高精度的差分格式。接下来我们介绍紧差分格式。这里继续以非齐次二阶双曲型偏微分方程的初边值问题为研究对象: 公式(1)中u表示一个与时间t和位置x有关的待求波函数,及方程右端项函数都是已知函数,是非零常数。 二、理论推导
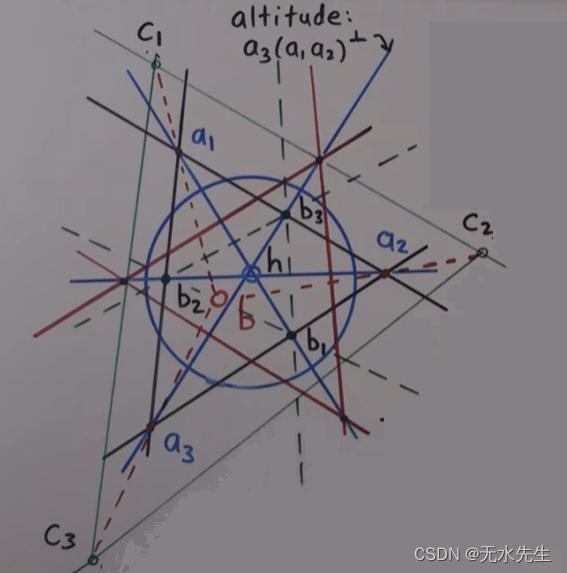
【双曲几何】圆盘上的三角形概念
目录 一、说明二、对偶三角形概念2.1 反演关系2.2 对偶关系2.3 找出三角形的对偶三角形 三、正交三角形概念3.1 通过对偶三角形,找到垂心3.2 正交三角形的概念3.3 中心射影点的概念 四、后记 一、说明 本文对双曲空间的三角形进行分析,本篇首先给出,参考圆内外的点映射,进而说明三角形形状的反演映射关系。进而给出正交三角图和射影中心的概念。我i们常常提到庞加莱盘的概念
偏微分方程算法之一阶双曲差分法
目录 一、研究目标 二、理论推导 2.1 引言 2.2 迎风格式 2.3 完全不稳定差分格式 2.4 蛙跳格式(Leapfrog) 2.5 Lax-Friedrichs格式 2.6 Lax-Wendroff格式 2.7 Beam-Warming格式 2.8 隐格式 2.9 Courant-Friedrichs-Lewy条件(CFL条件) 三、算例实现 3.1 迎风格式
【CVPR2022】双曲图像分割
来源:专知本文为论文,建议阅读5分钟双曲流形为图像分割提供了一个有价值的替代方案。 对于图像分割,目前的标准是通过线性超平面在欧几里德输出嵌入空间中进行像素级优化和推理。在这项工作中,我们表明双曲流形为图像分割提供了一个有价值的替代方案,并提出了一个易于处理的公式,层次像素级分类在双曲空间。双曲图像分割为分割开辟了新的可能性和实际的好处,如自由不确定性估计和边界信息,零标签泛化,提高了低维
基础的三角函数,反三角函数,双曲函数的图形绘制(matlab)
matlab基本图形绘制 基础的三角函数,反三角函数,双曲函数的图形绘制; 在此过程,可以熟悉基础的matlab指令; 三角函数 y1 = sin(x);y2 = cos(x);y3 = tan(x);plot(x,y1,'r')hold onplot(x,y2,'g')hold onplot(x,y3,'b');grid on xlabel('X')ylabel('Y'
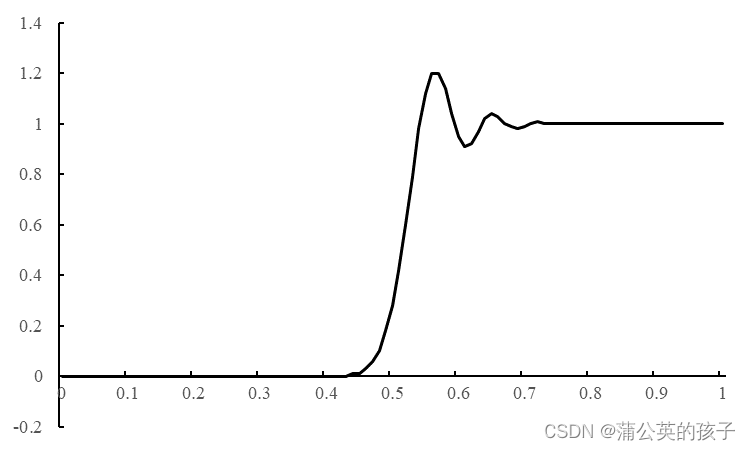
1.5C语言 双曲正弦函数(*) 优化麦克劳林公式
一.传统算法 #include<stdio.h>#include<math.h>int jc(int x);int main(){double x,eps,y=0.0;scanf("%lf%lf",&x,&eps);int de=1,i=1;double item=1.0;while(fabs(item)>=eps){item=pow(x,i)/jc(de);i+=2;y+=item;
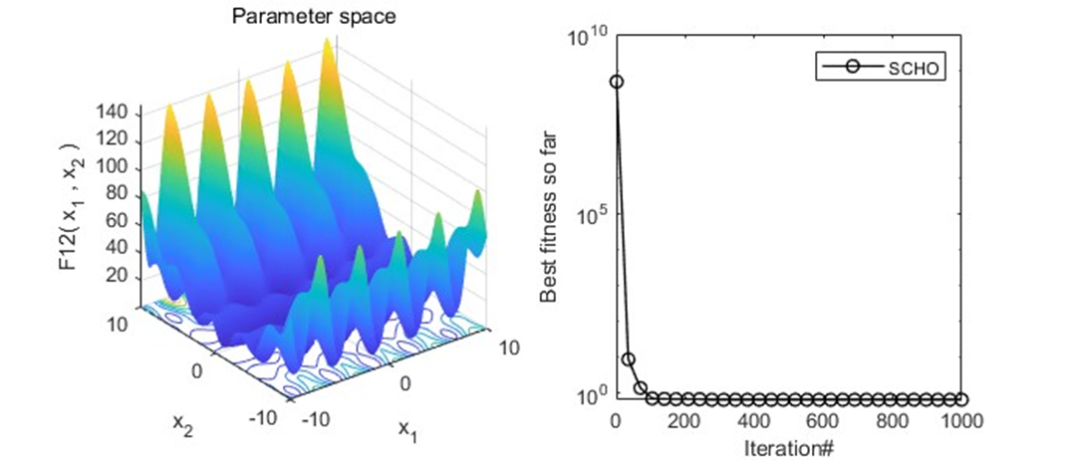
2023年智能算法之双曲正弦余弦优化器(SCHO),原理公式详解,附matlab代码
双曲正弦余弦优化器(Sinh Cosh Optimizer,SCHO)是一种新型元启发式算法,该算法基于双曲正弦和双曲余弦特性的数学启发,具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2023年10月发表在SCI一区,Top顶刊Knowledge-Based Systems上。 SCHO的灵感来源有三点。首先,如何在勘探和开发之间取得平衡是一个巨大的挑战,其次,面对复杂多样的问题,仍需