本文主要是介绍偏微分方程算法之一阶双曲差分法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、研究目标
二、理论推导
2.1 引言
2.2 迎风格式
2.3 完全不稳定差分格式
2.4 蛙跳格式(Leapfrog)
2.5 Lax-Friedrichs格式
2.6 Lax-Wendroff格式
2.7 Beam-Warming格式
2.8 隐格式
2.9 Courant-Friedrichs-Lewy条件(CFL条件)
三、算例实现
3.1 迎风格式
3.2 Lax-Friedrichs格式
3.3 Lax-Wendroff格式
3.4 Beam-Warming格式
四、结论
一、研究目标
上个专栏我们介绍了抛物型偏微分方程的代表算法的推导及算例实现。从今天开始,我们在新的专栏介绍另一种形式偏微分方程-双曲型的解法。
双曲型偏微分方程常用来描述波动和振动现象,常涉及复杂情况如激波、粘性等,主要应用于海洋、气象等流体力学的实际问题中。与抛物型偏微分方程相比,双曲型偏微分方程的特点是可以体现波的传播性质,描述波动或振动现象。
我们先以一阶双曲线型偏微分方程中最简单的线性模型作为研究对象,其定解可以仅有初始条件,也可以初边值条件都有。这里先讨论一阶对流方程,其半无界的初值问题为
其中,a为非零常数。
二、理论推导
2.1 引言
对于公式(1),可以验证其解析解为:
若将x看作是t的函数,则利用全微分公式可知,当
时,
。说明存在一族特征线:
为任意数,使得在这样的特征线上有
,即u为常数,
。也就是说,要获得在
平面上的任意一点
处的函数值
,只需将
沿特征线投影到x轴上得到投影点
,其中,
,则初始波形
在这一点的值
就等于
,如图1所示。
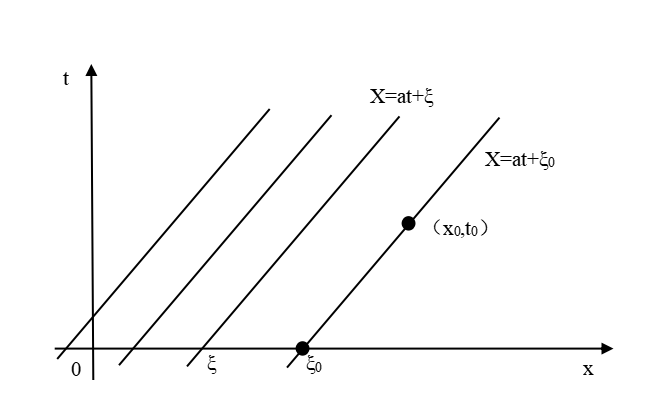
可见,任意一点处的函数值局部依赖于
在x轴上的投影点
处的初值。特征线
的方向代表了波的传播方向,当
时波向右传播,当
时波向左传播,但波形不变,波速为
。由此可知,公式(1)表示的是一个单向传播的波,也称作:单向波方程。
对公式(1)差分格式进行设计时,按照以下步骤:
1、网格剖分。在上半平面进行矩形网格剖分,分别取等距空间步长、时间步长为
,得到网格节点
其中
。
2、将原方程弱化。离散点上成立,即
3、处理偏导数。对偏导数用不同的差商近似建立不同的差分格式。将在2.2-2.7中进行介绍。
2.2 迎风格式
情形1:关于时间、空间的一阶偏导数均利用一阶向前差商进行近似,有
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(3)的局部阶段误差为,若记
,则公式(3)可以写作
稳定性条件为:,即
情形2:关于时间、空间的一阶偏导数分别利用一阶向前差商、一阶向后差商近似,有
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(4)的局部阶段误差为,若记
,则公式(4)可以写作
稳定性条件为:,即
联合两种情形的稳定性条件,可得迎风格式:
a<0时:
a>0时:
稳定性条件为:
事实上,公式(1)含有未知函数关于空间的一阶偏导数项,即对流项,虽然在数学理论上对其进行离散是可以的,但在物理过程中看这样是不合适的,因为对流作用带有强烈的方向性,所以对流项的离散是否合适直接影响数值格式的性能,也说明了迎风格式是使用了定向的单边差商。
2.3 完全不稳定差分格式
情形3:对空间的偏导数采用二阶中心差商近似,有
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(5)的局部阶段误差为,若记
,则公式(5)可以写作
该式的稳定性条件不成立,即不存在不依赖时间步长、空间步长的常数,使得Von Neumann条件成立。
2.4 蛙跳格式(Leapfrog)
情形4:对情形3进行改造,可对时间、空间的偏导数均采用二阶中心差商近似,有
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(6)的局部阶段误差为,若记
,则公式(6)可以写作
稳定性条件为:
蛙跳格式是三层格式,不能自启动计算,需要用一个二阶的格式算出第一层信息,然后再利用蛙跳格式进行后面时间层的计算。
2.5 Lax-Friedrichs格式
情形5:在情形3中修改关于时间的一阶偏导数,将用其左右相邻两节点的算数平均来近似,即
关于空间的一阶偏导数用二阶中心差商,即
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(8)的局部阶段误差为,若记
,则公式(8)可以写作
稳定性条件为:
当r取常数时,Lax-Friedrichs是一阶格式。
2.6 Lax-Wendroff格式
此格式通过泰勒公式即原方程变形得到。由公式(1)可知:
及
根据泰勒公式有
将上式中的一阶偏导数、二阶偏导数用中心差商近似,精确解 用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(11)的局部阶段误差为,若记
,则公式(11)可以写作
稳定性条件为:
2.7 Beam-Warming格式
当时,公式(10)仍成立,式中
、
取迎风形式且兼顾高阶项,即
将上面两式代入公式(10)得
精确解用数值解
代替,并忽略高阶项,可得到
时的Beam-Warming格式:
公式(12)的局部阶段误差为。
稳定性条件为:
同理可得当时的Beam-Warming格式:
稳定性条件为:
2.8 隐格式
2-2至2-7所介绍的格式均为显格式,所以必须附加稳定性条件才能确保数值解最终收敛至精确解,而隐格式的稳定性更好,考虑通过设计隐格式来求解。
如当时,修改情形3中完全不稳定的显格式为隐格式,即关于时间和空间的一阶偏导数分别利用一阶向后差商和二阶中心差商近似,有:
将公式(2)中的精确解用数值解
代替,并忽略高阶项,可得到相应的数值格式:
公式(14)的局部阶段误差为,简化为:
或者
2.9 Courant-Friedrichs-Lewy条件(CFL条件)
CFL条件是差分格式收敛的一个必要条件,其本质上是原方程解的依赖区间必须包含于差分格式解的依赖区间。
以的迎风格式为例,公式(1)的精确解
在网格节点
处的值只依赖于过这一点的特征线在x轴上的投影点
处的初值,从而
是
在点
处的依赖区域(一个点)。而差分格式的式
的解在点处的值
依赖于前一时间层上的
,而
又分别依赖于更前一层上的
和
,以此类推,可得
依赖于初始时间层上的
,这样,数值解
的依赖区域是区间
,或者说上式的解
的依赖区域为
。再考察数值解于精确解依赖区域的关系可知,在点
处,如果精确解的依赖区域
在区间
之外,那么上式计算出来的解就和原方程-公式(1)的解毫无关系,因此这个数值格式的解不可能收敛到原方程的解。所以,数值解收敛到精确解的一个必要条件就是
,意味着
,即
,也就是上式的稳定性条件。换言之,CFL条件与稳定性条件一致。
三、算例实现
求解一阶对流方程初值问题:
其中,初值在x=0处间断,取空间、时间步长分别为
,给出t=0.5时
区间内数值的图像。
(精确解为且对应上述空间、时间步长的选取易得r=0.5)
3.1 迎风格式
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int j,k,m,n;double a, h, tau, r, *x, *t, * *u;double phi(double x);double exact(double x, double t);m=300;n=200;h=3.0/m;tau=1.0/n;a=1.0;r=a*tau/h;printf("r=%.4f.\n", r);if(r>1.0){printf("stability condition is not satisfied!\n");exit(0);}x=(double *)malloc(sizeof(double)*(m+1));t=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)x[j]=-1.0+j*h;for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(j=0;j<=m;j++)u[j]=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)u[j][0]=phi(x[j]);for(k=0;k<n;k++){for(j=k+1;j<=m;j++)u[j][k+1]=r*u[j-1][k]+(1.0-r)*u[j][k];}for (j = 100; j <= 200; j++){printf("x=%.2f, y=%.2f\n", x[j], u[j][n/2]); }free(x); free(t);for(j=0;j<=m;j++)free(u[j]);free(u);return 0;
}double phi(double x)
{if(x<=0)return 0.0;elsereturn 1.0;
}
double exact(double x, double t)
{if (x <= t)return 0.0;elsereturn 1.0;
}计算结果如下:
r=0.5000.
x=0.00, y=0.00
x=0.01, y=0.00
x=0.02, y=0.00
x=0.03, y=0.00
x=0.04, y=0.00
x=0.05, y=0.00
x=0.06, y=0.00
x=0.07, y=0.00
x=0.08, y=0.00
x=0.09, y=0.00
x=0.10, y=0.00
x=0.11, y=0.00
x=0.12, y=0.00
x=0.13, y=0.00
x=0.14, y=0.00
x=0.15, y=0.00
x=0.16, y=0.00
x=0.17, y=0.00
x=0.18, y=0.00
x=0.19, y=0.00
x=0.20, y=0.00
x=0.21, y=0.00
x=0.22, y=0.00
x=0.23, y=0.00
x=0.24, y=0.00
x=0.25, y=0.00
x=0.26, y=0.00
x=0.27, y=0.00
x=0.28, y=0.00
x=0.29, y=0.00
x=0.30, y=0.00
x=0.31, y=0.00
x=0.32, y=0.00
x=0.33, y=0.00
x=0.34, y=0.00
x=0.35, y=0.00
x=0.36, y=0.00
x=0.37, y=0.00
x=0.38, y=0.01
x=0.39, y=0.01
x=0.40, y=0.02
x=0.41, y=0.03
x=0.42, y=0.04
x=0.43, y=0.07
x=0.44, y=0.10
x=0.45, y=0.14
x=0.46, y=0.18
x=0.47, y=0.24
x=0.48, y=0.31
x=0.49, y=0.38
x=0.50, y=0.46
x=0.51, y=0.54
x=0.52, y=0.62
x=0.53, y=0.69
x=0.54, y=0.76
x=0.55, y=0.82
x=0.56, y=0.86
x=0.57, y=0.90
x=0.58, y=0.93
x=0.59, y=0.96
x=0.60, y=0.97
x=0.61, y=0.98
x=0.62, y=0.99
x=0.63, y=0.99
x=0.64, y=1.00
x=0.65, y=1.00
x=0.66, y=1.00
x=0.67, y=1.00
x=0.68, y=1.00
x=0.69, y=1.00
x=0.70, y=1.00
x=0.71, y=1.00
x=0.72, y=1.00
x=0.73, y=1.00
x=0.74, y=1.00
x=0.75, y=1.00
x=0.76, y=1.00
x=0.77, y=1.00
x=0.78, y=1.00
x=0.79, y=1.00
x=0.80, y=1.00
x=0.81, y=1.00
x=0.82, y=1.00
x=0.83, y=1.00
x=0.84, y=1.00
x=0.85, y=1.00
x=0.86, y=1.00
x=0.87, y=1.00
x=0.88, y=1.00
x=0.89, y=1.00
x=0.90, y=1.00
x=0.91, y=1.00
x=0.92, y=1.00
x=0.93, y=1.00
x=0.94, y=1.00
x=0.95, y=1.00
x=0.96, y=1.00
x=0.97, y=1.00
x=0.98, y=1.00
x=0.99, y=1.00
x=1.00, y=1.003.2 Lax-Friedrichs格式
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int j,k,m,n;double a, h, tau, r, *x, *t, **u;double phi(double x);double exact(double x, double t);m=300;n=200;h=3.0/m;tau=1.0/n;a=1.0;r=a*tau/h;printf("r=%.4f.\n", r);if(r>1.0){printf("stability condition is not satisfied!\n");exit(0);}x=(double *)malloc(sizeof(double)*(m+1));t=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)x[j]=-1.0+j*h;for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(j=0;j<=m;j++)u[j]=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)u[j][0]=phi(x[j]);for(k=0;k<n;k++){for(j=k+1;j<=m-(k+1);j++)u[j][k+1]=(1.0+r)*u[j-1][k]/2.0+(1.0-r)*u[j+1][k]/2;}for(j=100;j<=200;j++){printf("x=%.2f, y=%.2f\n", x[j], u[j][n/2]);}free(x); free(t);for(j=0;j<=m;j++)free(u[j]);free(u);return 0;
}double phi(double x)
{if(x<=0)return 0.0;elsereturn 1.0;
}
double exact(double x, double t)
{if(x<=t)return 0.0;elsereturn 1.0;
}计算结果如下:
r=0.5000.
x=0.00, y=0.00
x=0.01, y=0.00
x=0.02, y=0.00
x=0.03, y=0.00
x=0.04, y=0.00
x=0.05, y=0.00
x=0.06, y=0.00
x=0.07, y=0.00
x=0.08, y=0.00
x=0.09, y=0.00
x=0.10, y=0.00
x=0.11, y=0.00
x=0.12, y=0.00
x=0.13, y=0.00
x=0.14, y=0.00
x=0.15, y=0.00
x=0.16, y=0.00
x=0.17, y=0.00
x=0.18, y=0.00
x=0.19, y=0.00
x=0.20, y=0.00
x=0.21, y=0.00
x=0.22, y=0.00
x=0.23, y=0.00
x=0.24, y=0.00
x=0.25, y=0.00
x=0.26, y=0.00
x=0.27, y=0.01
x=0.28, y=0.01
x=0.29, y=0.01
x=0.30, y=0.01
x=0.31, y=0.02
x=0.32, y=0.02
x=0.33, y=0.03
x=0.34, y=0.03
x=0.35, y=0.04
x=0.36, y=0.04
x=0.37, y=0.07
x=0.38, y=0.07
x=0.39, y=0.10
x=0.40, y=0.10
x=0.41, y=0.15
x=0.42, y=0.15
x=0.43, y=0.21
x=0.44, y=0.21
x=0.45, y=0.28
x=0.46, y=0.28
x=0.47, y=0.36
x=0.48, y=0.36
x=0.49, y=0.45
x=0.50, y=0.45
x=0.51, y=0.54
x=0.52, y=0.54
x=0.53, y=0.63
x=0.54, y=0.63
x=0.55, y=0.71
x=0.56, y=0.71
x=0.57, y=0.79
x=0.58, y=0.79
x=0.59, y=0.85
x=0.60, y=0.85
x=0.61, y=0.90
x=0.62, y=0.90
x=0.63, y=0.94
x=0.64, y=0.94
x=0.65, y=0.96
x=0.66, y=0.96
x=0.67, y=0.98
x=0.68, y=0.98
x=0.69, y=0.99
x=0.70, y=0.99
x=0.71, y=0.99
x=0.72, y=0.99
x=0.73, y=1.00
x=0.74, y=1.00
x=0.75, y=1.00
x=0.76, y=1.00
x=0.77, y=1.00
x=0.78, y=1.00
x=0.79, y=1.00
x=0.80, y=1.00
x=0.81, y=1.00
x=0.82, y=1.00
x=0.83, y=1.00
x=0.84, y=1.00
x=0.85, y=1.00
x=0.86, y=1.00
x=0.87, y=1.00
x=0.88, y=1.00
x=0.89, y=1.00
x=0.90, y=1.00
x=0.91, y=1.00
x=0.92, y=1.00
x=0.93, y=1.00
x=0.94, y=1.00
x=0.95, y=1.00
x=0.96, y=1.00
x=0.97, y=1.00
x=0.98, y=1.00
x=0.99, y=1.00
x=1.00, y=1.003.3 Lax-Wendroff格式
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int j,k,m,n;double a, h, tau, r, *x, *t, **u;double phi(double x);double exact(double x, double t);m=300;n=200;h=3.0/m;tau=1.0/n;a=1.0;r=a*tau/h;printf("r=%.4f.\n", r);if(r>1.0){printf("stability condition is not satisfied!\n");exit(0);}x=(double *)malloc(sizeof(double)*(m+1));t=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)x[j]=-1.0+j*h;for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(j=0;j<=m;j++)u[j]=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)u[j][0]=phi(x[j]);for(k=0;k<n;k++){for(j=k+1;j<=m-(k+1);j++)u[j][k+1]=(1.0+r)*r*u[j-1][k]/2.0+(1.0-r*r)*u[j][k]+r*(r-1.0)*u[j+1][k]/2;}for(j=100;j<=200;j++){printf("x=%.2f, y=%.2f\n", x[j],u[j][n/2]);}free(x); free(t);for(j=0;j<=m;j++)free(u[j]);free(u);return 0;
}double phi(double x)
{if(x<=0)return 0.0;elsereturn 1.0;
}
double exact(double x, double t)
{if(x<=t)return 0.0;elsereturn 1.0;
}计算结果如下:
r=0.5000.
x=0.00, y=-0.00
x=0.01, y=-0.00
x=0.02, y=0.00
x=0.03, y=0.00
x=0.04, y=-0.00
x=0.05, y=-0.00
x=0.06, y=0.00
x=0.07, y=0.00
x=0.08, y=-0.00
x=0.09, y=-0.00
x=0.10, y=0.00
x=0.11, y=0.00
x=0.12, y=0.00
x=0.13, y=-0.00
x=0.14, y=-0.00
x=0.15, y=0.00
x=0.16, y=0.00
x=0.17, y=-0.00
x=0.18, y=-0.00
x=0.19, y=-0.00
x=0.20, y=0.00
x=0.21, y=0.00
x=0.22, y=-0.00
x=0.23, y=-0.00
x=0.24, y=-0.00
x=0.25, y=0.00
x=0.26, y=0.00
x=0.27, y=0.00
x=0.28, y=-0.00
x=0.29, y=-0.01
x=0.30, y=-0.00
x=0.31, y=0.01
x=0.32, y=0.02
x=0.33, y=0.01
x=0.34, y=-0.00
x=0.35, y=-0.03
x=0.36, y=-0.04
x=0.37, y=-0.02
x=0.38, y=0.03
x=0.39, y=0.08
x=0.40, y=0.09
x=0.41, y=0.05
x=0.42, y=-0.04
x=0.43, y=-0.14
x=0.44, y=-0.20
x=0.45, y=-0.20
x=0.46, y=-0.12
x=0.47, y=0.02
x=0.48, y=0.21
x=0.49, y=0.40
x=0.50, y=0.58
x=0.51, y=0.72
x=0.52, y=0.82
x=0.53, y=0.90
x=0.54, y=0.94
x=0.55, y=0.97
x=0.56, y=0.99
x=0.57, y=0.99
x=0.58, y=1.00
x=0.59, y=1.00
x=0.60, y=1.00
x=0.61, y=1.00
x=0.62, y=1.00
x=0.63, y=1.00
x=0.64, y=1.00
x=0.65, y=1.00
x=0.66, y=1.00
x=0.67, y=1.00
x=0.68, y=1.00
x=0.69, y=1.00
x=0.70, y=1.00
x=0.71, y=1.00
x=0.72, y=1.00
x=0.73, y=1.00
x=0.74, y=1.00
x=0.75, y=1.00
x=0.76, y=1.00
x=0.77, y=1.00
x=0.78, y=1.00
x=0.79, y=1.00
x=0.80, y=1.00
x=0.81, y=1.00
x=0.82, y=1.00
x=0.83, y=1.00
x=0.84, y=1.00
x=0.85, y=1.00
x=0.86, y=1.00
x=0.87, y=1.00
x=0.88, y=1.00
x=0.89, y=1.00
x=0.90, y=1.00
x=0.91, y=1.00
x=0.92, y=1.00
x=0.93, y=1.00
x=0.94, y=1.00
x=0.95, y=1.00
x=0.96, y=1.00
x=0.97, y=1.00
x=0.98, y=1.00
x=0.99, y=1.00
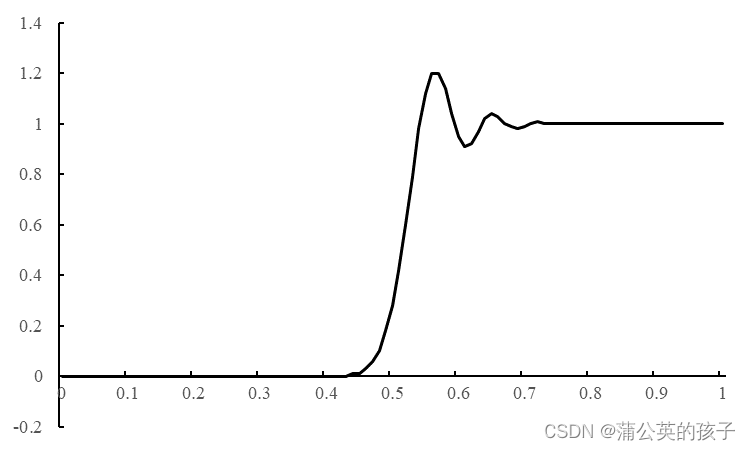
x=1.00, y=1.003.4 Beam-Warming格式
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int j,k,m,n;double a, h, tau, r, *x, *t, **u;double phi(double x);double exact(double x, double t);m=400;n=200;h=4.0/m;tau=1.0/n;a=1.0;r=a*tau/h;printf("r=%.4f.\n", r);if(r>2.0){printf("stability condition is not satisfied!\n");exit(0);}x=(double *)malloc(sizeof(double)*(m+1));t=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)x[j]=-2.0+j*h;for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(j=0;j<=m;j++)u[j]=(double *)malloc(sizeof(double)*(n+1));for(j=0;j<=m;j++)u[j][0]=phi(x[j]);for(k=0;k<n;k++){for(j=(k+1)*2;j<=m;j++)u[j][k+1]=-r*(1.0-r)*u[j-2][k]/2.0+(2.0-r)*r*u[j-1][k]+(1.0-r)*(2.0-r)*u[j][k]/2.0;}for(j=200;j<=300;j++){printf("x=%.2f, y=%.2f\n", x[j],u[j][n/2]);}free(x); free(t);for(j=0;j<=m;j++)free(u[j]);free(u);return 0;
}double phi(double x)
{if(x<=0)return 0.0;elsereturn 1.0;
}
double exact(double x, double t)
{if(x<=t)return 0.0;elsereturn 1.0;
}计算结果如下:
r=0.5000.
x=0.00, y=0.00
x=0.01, y=0.00
x=0.02, y=0.00
x=0.03, y=0.00
x=0.04, y=0.00
x=0.05, y=0.00
x=0.06, y=0.00
x=0.07, y=0.00
x=0.08, y=0.00
x=0.09, y=0.00
x=0.10, y=0.00
x=0.11, y=0.00
x=0.12, y=0.00
x=0.13, y=0.00
x=0.14, y=0.00
x=0.15, y=0.00
x=0.16, y=0.00
x=0.17, y=0.00
x=0.18, y=0.00
x=0.19, y=0.00
x=0.20, y=0.00
x=0.21, y=0.00
x=0.22, y=0.00
x=0.23, y=0.00
x=0.24, y=0.00
x=0.25, y=0.00
x=0.26, y=0.00
x=0.27, y=0.00
x=0.28, y=0.00
x=0.29, y=0.00
x=0.30, y=0.00
x=0.31, y=0.00
x=0.32, y=0.00
x=0.33, y=0.00
x=0.34, y=0.00
x=0.35, y=0.00
x=0.36, y=0.00
x=0.37, y=0.00
x=0.38, y=0.00
x=0.39, y=0.00
x=0.40, y=0.00
x=0.41, y=0.00
x=0.42, y=0.00
x=0.43, y=0.00
x=0.44, y=0.01
x=0.45, y=0.01
x=0.46, y=0.03
x=0.47, y=0.06
x=0.48, y=0.10
x=0.49, y=0.18
x=0.50, y=0.28
x=0.51, y=0.42
x=0.52, y=0.60
x=0.53, y=0.79
x=0.54, y=0.98
x=0.55, y=1.12
x=0.56, y=1.20
x=0.57, y=1.20
x=0.58, y=1.14
x=0.59, y=1.04
x=0.60, y=0.95
x=0.61, y=0.91
x=0.62, y=0.92
x=0.63, y=0.97
x=0.64, y=1.02
x=0.65, y=1.04
x=0.66, y=1.03
x=0.67, y=1.00
x=0.68, y=0.99
x=0.69, y=0.98
x=0.70, y=0.99
x=0.71, y=1.00
x=0.72, y=1.01
x=0.73, y=1.00
x=0.74, y=1.00
x=0.75, y=1.00
x=0.76, y=1.00
x=0.77, y=1.00
x=0.78, y=1.00
x=0.79, y=1.00
x=0.80, y=1.00
x=0.81, y=1.00
x=0.82, y=1.00
x=0.83, y=1.00
x=0.84, y=1.00
x=0.85, y=1.00
x=0.86, y=1.00
x=0.87, y=1.00
x=0.88, y=1.00
x=0.89, y=1.00
x=0.90, y=1.00
x=0.91, y=1.00
x=0.92, y=1.00
x=0.93, y=1.00
x=0.94, y=1.00
x=0.95, y=1.00
x=0.96, y=1.00
x=0.97, y=1.00
x=0.98, y=1.00
x=0.99, y=1.00
x=1.00, y=1.00四、结论
对四种不同格式的计算结果绘图,并与精确解进行对比,有:
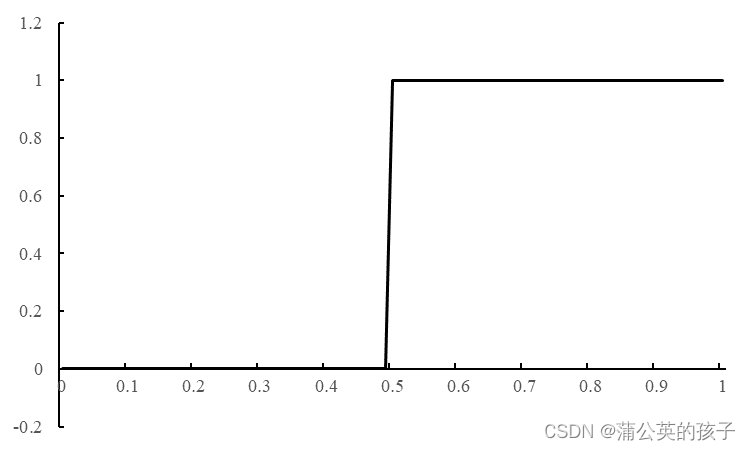
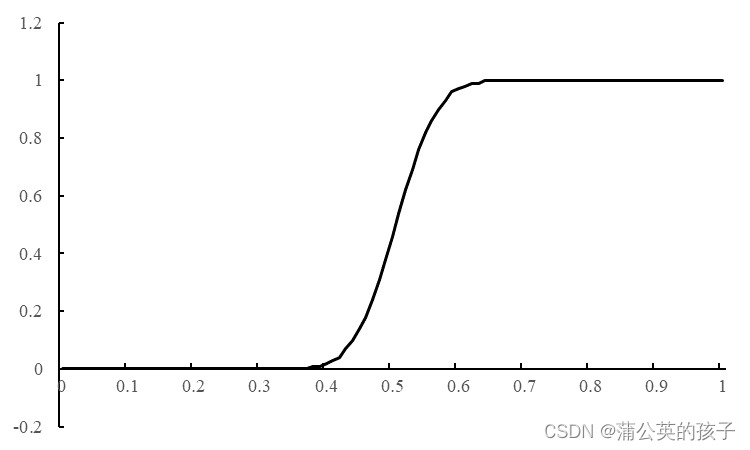
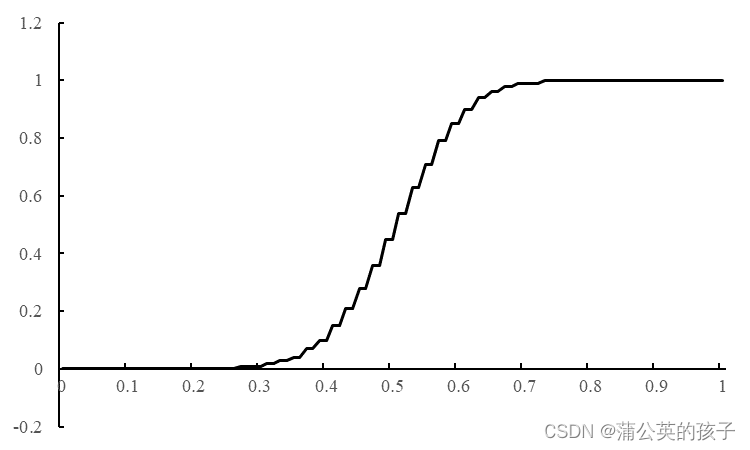

这篇关于偏微分方程算法之一阶双曲差分法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








