根号专题
Python实现开根号的五种方式
《Python实现开根号的五种方式》在日常数据处理、数学计算甚至算法题中,开根号是一个高频操作,但你知道吗?Python中实现开根号的方式远不止一种!本文总结了5种常用方法,感兴趣的小伙伴跟着小编一起... 目录一、为什么需要多种开根号方式?二、5种开根号方式详解方法1:数学库 math.sqrt() ——
第11讲-项目四-双精度浮点数的和、平均值、平方和以及平方和开根号
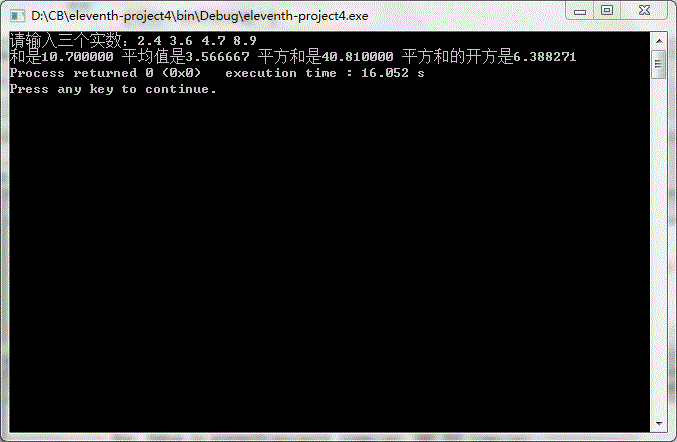
任务和代码 /**Copyright (c)2015,CSDN学院*All rights reserved.*文件名称:main.c*作 者:胡先军*完成日期:2015年4月27日*版 本 号:v1.0**问题描述:输入3个双精度实数,求出它们的和、平均值、平方和以及平方和的开方*程序输出:4个结果*/#include <stdio.h>#include <mat
transfomer中attention为什么要除以根号d_k
简介 得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下: A t t e n t i o n ( Q , K , V ) = S o f t m a x ( Q K T d k ) V Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=Softmax(dk
为什么self-attention要除以一个根号dk
简单说法是为了让方差到1,推公式也好推。但是没几个人说为什么方差要到1. 如果不除以根号dk,显然QK有可能很大,这就让softmax更有能力得到接近one-hot的结果。这本应是好的,但是从实践来看,我们并不要求一定要输出one-hot,这有点over-fitting的感觉了。差不多就行。 还有更重要的理由。softmax求导是 a − a 2 a-a^2 a−a2, a a a是softmax
Python金融实战一:用Python 完成普通计算器的功能——删除变量 加减乘除 调用math命令进行开根号 幂函数 对数函数 dir()查找 以及选择合适精度(含代码和结果)
用Python 完成普通计算器的功能 1. 删除或取消变量 pv = 22r = 0.1n = 5del(n)print(n)结果:NameError: name 'n' is not defined 2.加减乘除 s=3.09+2.1*5.2-3/0.56print(s)结果8.652857142857144 如果意外输出两次//,会得到奇怪的结果,双斜杠代表整数除法,结
计算2½(根号2)-----二分法解决
解题思路 既然要求2½的值,可以首先确定的是值的范围在1~2之间,所以可以 确定区间为[1,2],如果mid>2½,令right=mid;,如果mid<2½,令left=mid,所以之间可以借助函数f(x)=x*x来实现。 代码 实现 //由于2½是无理数,所以只能获取近似值,这里不妨以精度1e-5为例const double esp=1e-5;double f(double
python中根号怎么表示_python中根号怎么表示
sqrt() 方法返回数字x的平方根。 以下是 sqrt() 方法的语法:(推荐学习:Python视频教程)import math math.sqrt( x ) 注意:sqrt()是不能直接访问的,需要导入 math 模块,通过静态对象调用该方法。 参数 x -- 数值表达式。 返回值 返回数字x的平方根。 实例 以下展示了使用 sqrt() 方法的实例:#!/usr/bin
self-attention为什么要除以根号d_k
一、因为softmax的输入很大时,其梯度会变的很小,趋近于0; 二、除以根号Dk的目的就是使得,QK/Dk满足方差稳定到1,使得softmax的梯度不至于太小 参考: transformer中的attention为什么scaled? - 知乎 注意力机制在softmax时除以一个根号d的作用_samuelzhoudev的博客-CSDN博客 self-attention为什么要
证明之根号2的无理性
根号2的无理性 反证法的力量:证明 2 \sqrt{2} 2 是无理数的奇妙之旅 我在上一个系列中说到,一个数如果可以写成分数p/q(其中p和q是整数)的形式则称为有理数,若不可以则称为无理数。数学中一条著名的证明表明了 2 \sqrt{2} 2 是无理数。这项证明阐释了反证法这种技术,即通过推出矛盾来证明。 这样的证明以假设要证的结论为假开始。这看似有点奇怪,但其实我们在日常对话
洛谷 P3396 哈希冲突(根号算法 分块)
P3396 哈希冲突 题目链接 从这篇博客来做的这道题 分析: 看到这个题的数据范围是有点懵,这能怎么做啊? 先看暴力 O ( n 2 ) O(n^2) O(n2) , for (int i = x; i <= n; i += p)ans += value[i]; 如果我们做预处理的话, a n s [ p ] [ x ] ans[p][x] ans[p][x] , % p \%p
[BZOJ2956]模积和-根号分块
说在前面 突然觉得”说在前面”里的废话真是太多了= = 题目 BZOJ2956传送门 题目大意 给定 N N,MM,求出 ∑i=1N∑j=1M(Nmodi)⋅(Mmodj)[i!=j] \sum\limits_{i=1}^{N}\sum\limits_{j=1}^{M}\left(N\bmod i\right)\cdot \left(M\bmod j\right)[i!=j] 在模1
visio打出根号,下标,并调整符号的大小
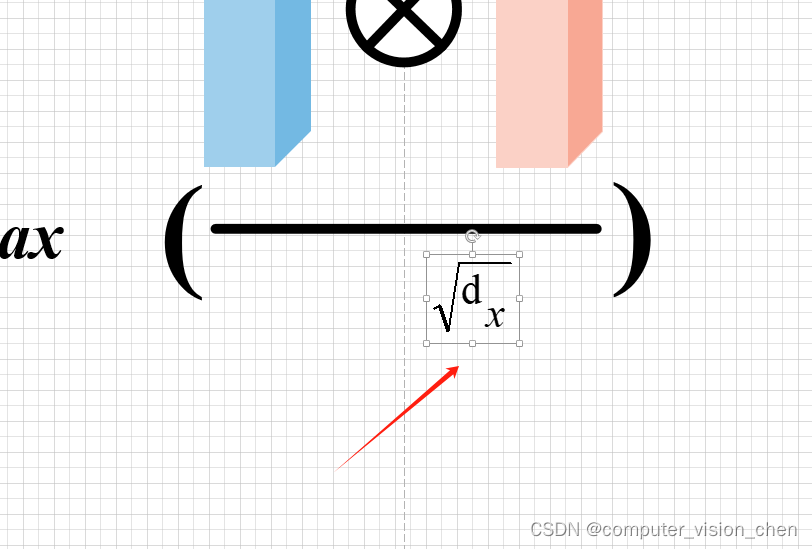
插入公式对象 打出根号和带下标的字母 调整符号大小 把做好的公式符号弄到visio中的图中 ctrl+a 复制符号 进入visio中粘贴 并 调整大小 调整大小直接拖动边框上的圆点即可。
乐鑫笔试题-----开根号
类似https://blog.csdn.net/SHAOYEZUIZUISHAUI/article/details/106452586 //注意审题:不用任何数学库函数,所以我们只用加减乘除#include <iostream>using namespace std;//二分搜索求开n次方//double epr = 10E-14;#define epr 10
[LUOGU 哈希冲突] 巧妙根号算法
题目: 题目链接:[LUOGU 哈希冲突] 题解: 一看到是rxz大佬的题目,,就上去做了做,但是,,为什么挂出来分块的标签,但是呢,,,,跟分块,,一点关系都没有啊!!!!! 不瞎扯了,,,进入正题,,, 先解释一下题面: 就是给你一串数,对于标号进行操作,标号取模得x的,把他给的数的劝权值进行取和。 就是 n n n\sqrt{n} nn 进行预处理,之后的可以 O ( 1 ) O(
CF342E Xenia and Tree 题解 (根号算法,操作分块)
题目 题面 简要题意: 给定一棵 n n n 个节点的树,初始时 1 1 1 号节点为红色,其余为蓝色。 要求支持如下操作: 1. 将一个节点变为红色。 2. 询问节点 u u u 到最近红色节点的距离。 共 q q q 次操作。 1 ≤ n , q ≤ 1 0 5 1 \leq n, q \leq
编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...
Python计算的位数 在电脑上做了一个实验,看看python能计算到多少位,一下是结果。 x = math.sqrt((3)) print ("%.53f"%(x)) print ("%.63f"%(x)) print ("%.83f"%(x)) 1.73205080756887719317660412343684583902359008789062500 1.7320508075688771
点分治维护dp+连通块上新型dp思路+乘积方面进行根号dp:0922T4
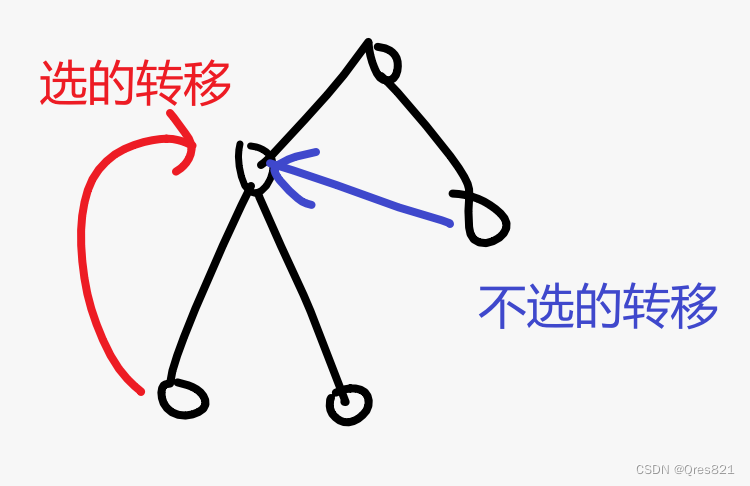
首先连通块,所以点分治肯定是 Trick1 钦定选根的连通块dp 对于钦定选根的连通块dp,有一种常见思路 先对原树求其dfn序,按dfn序倒序求解 具体的,对于当前点 i i i(注意这里都是指dfn序),我们可以钦定 i i i 是否选 如果 i i i 选,就由 i + 1 i+1 i+1,也就是 i i i 的第一个儿子转移过来(因为只有他选他子树才可能被选) 如果
latext 开根号_LaTeX 中插入数学公式
一、常用的数学符号 1、小写希腊字母 \alpha \nu \beta \xi \gamma o \delta \pi \epsilon \rho \zeta \sigma \eta \tau \theta \upsilon \iota \phi \kappa \chi \lambda \psi \mu \omega 2、大写希腊字母 大写希腊字母
几何画板里怎样打根号符号
在几何画板中,我们常常需要编辑带根号的数字或者绘制带根号的函数图像,那么怎么才能很轻松地就编辑出来呢?下面将通过举例详细介绍几何画板根号的编辑方法。 一、编辑带根号的数字 打开几何画板,选择“文本工具”,在画板上拖出一个文本框,在文字输入状态下,点击下方的“符号面板”按钮,接着在弹出的模板中选择根号模板,这样就可以打出带根号的数字。 在符号面板下选择根号模板打出根号示例 二、绘制带根号的函数图
latext 开根号_LaTeX技巧576:封闭根符号
有些人喜欢平方根“关闭”,里面写内容。这种方法可以使得根号的范围更加清晰,所开根正是在根号的范围。 如: 在连接中给出一个很好的解决方案,定义\ sqrt。然而,维基百科又讲到: 当你想使用多次根式时,不幸的是,这个命令就不能正常运行了。比如输入\ sqrt[B]{A}... ...你会得到一个错误的输出。换句话说,只有当你的整个文档中没有多次根式的时候,你可以这样重新定义的平方根这样。 该怎么
2-5 jmu-Java-01入门-开根号 (20分)
使用逐步逼近法对给定数值x求开根号。 逐步逼近法说明: 从0开始逐步累加步长值。 步长=0.0001,epsilon(误差)=0.0001 循环继续的条件: 平方值<x 且 |x-平方值| > epsilon ###说明与参考 数值输出保留6位小数,使用System.out.printf("%.6f\n") 求平方,参考Math.pow函数。 输入值<0时,返回Double.NaN 输入
如何证明根号2,3是无理数
1.问题 推广成,如何证明 根号 p(p是素数)是无理数 素数:一个大于1的自然数,如果除了1和它自身外,不能被其他自然数整除(除0以外)的数称之为素数。 2.思路 反证法: 假如 ( p ) = a b \sqrt{(p)} = \frac{a}{b} (p) =ba 其中, a, b互质的整数。 然后, a 2 = p b 2 a^2 = p b^2 a2=pb2 假如 a
python: 估算根号二的五种算法和实例
1.法一 夹逼法(自创) 算法来源(56条消息) 如何算根号2_根号2怎么算_光哥_帅的博客-CSDN博客 上文使用了一个比较巧妙的方法迭代逼近根号二 用y1和y2夹逼根号2 def fun(t):y1, y2 = 1, 2x = 1for i in range(t):y1 = xy2 = 2 / y1x = (y1 + y2) / 2return xprin







![[BZOJ2956]模积和-根号分块](https://img-blog.csdn.net/20171201201944656?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvSXp1bWlfSGFuYWtv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)

![编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...](https://img-blog.csdnimg.cn/img_convert/783bc90990f846659eddfcbd0692f8ee.png)