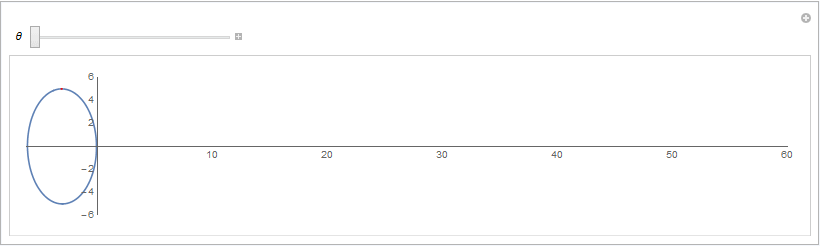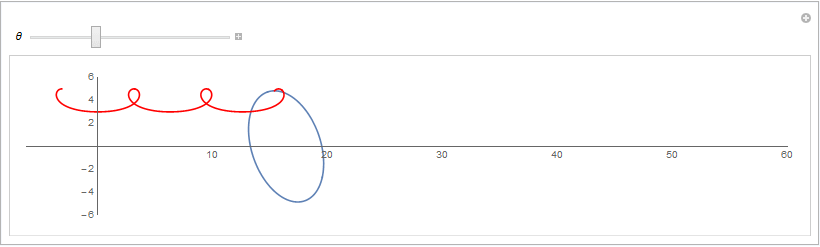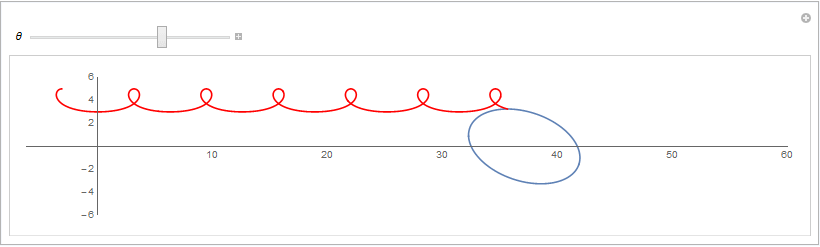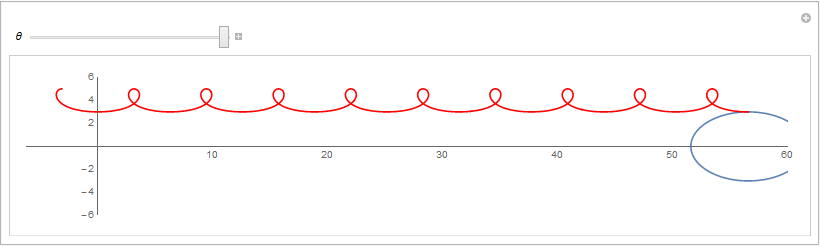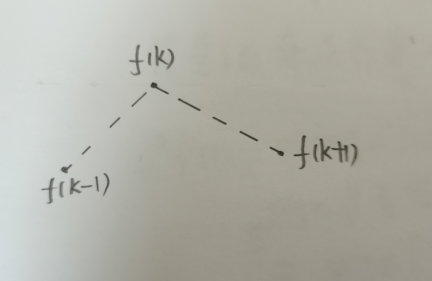极大值专题

非极大值抑制(NMS)的原理理解

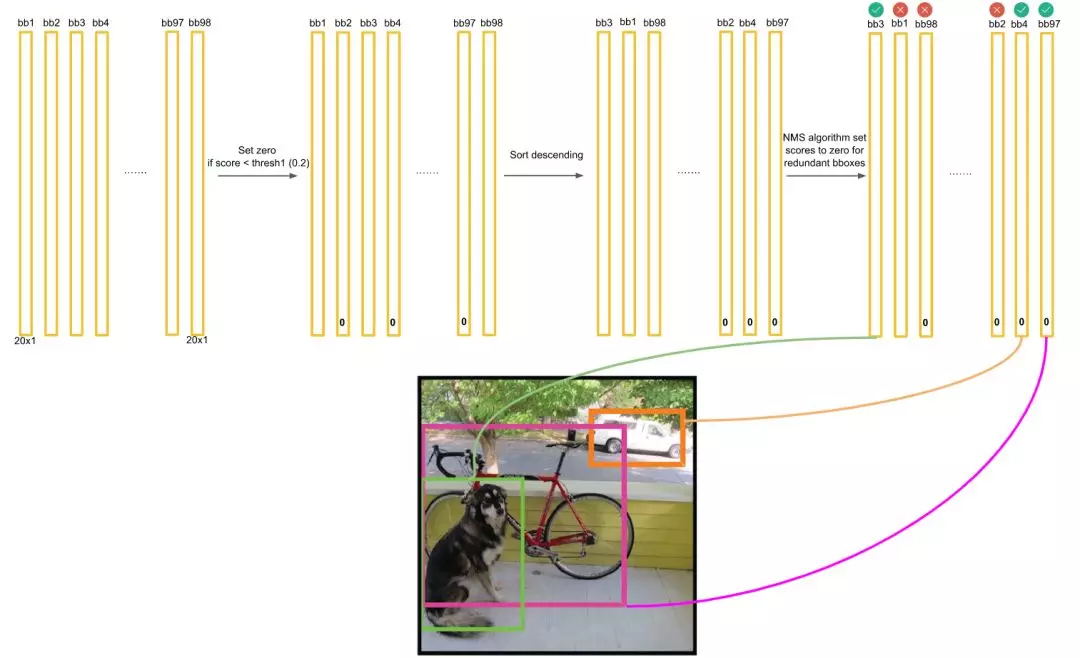
假设有ABCDEF这么多个得分框（已经按照得分从小到大排序）。 1、从最大概率矩形框F开始，分别判断A~E与F的重叠度IOU是否大于某个设定的阈值; 2、假设B、D与F的重叠度超过阈值，那么就扔掉B、D；并标记第一个矩形框F，是我们保留下来的。 3、从剩下的矩形框A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，重叠度大于一定的阈值，那么就扔掉；并标记E是我们保留下来的第二个矩形框

每天五分钟计算机视觉：使用极大值抑制来寻找最优的目标检测对象

本文重点在目标检测领域，当模型预测出多个候选框（bounding boxes）时，我们需要一种方法来确定哪些候选框最有可能表示真实的目标。由于模型的不完美性和图像中目标的重叠性，往往会有多个候选框对应于同一个目标。此时，极大值抑制（Non-Maximum Suppression，NMS）技术就显得尤为重要。目标检测算法使用19*19的网络对图片进行处理首先我们应该知道，一个

【数字信号去噪】基于matlab小波模极大值数字信号去躁【含Matlab源码 2602期】

✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。 🍎个人主页：海神之光 🏆代码获取方式：海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭：行百里者，半于九十。更多Matlab仿真内容点击👇 Matlab图像处理（进阶版）路径规划（Matlab）神经网络预测与分类（Matlab）优化求解（Matlab）语音处理（Matlab

NMS(非极大值抑制)在物体检测中的应用

转自：http://blog.csdn.net/running_j/article/details/51727350 非极大值抑制在物体检测方面的应用结合faster-rcnn给出的py_cpu_nms.py的源码来介绍一下nms算法在物体检测方面的应用。faster-rcnn中经过rpn层之后会得到一些boundingbox和boundingbox对应的属于某一类的分数（置信度）。所

原来椭圆在平移的同时绕型心旋转,极大值点的轨迹是漂亮的曲线

下图所用的参数; 椭圆标准情况下参数方程用 ( 5 cos(t), 3 sin(t) ) 假设的旋转角速度为 \theta, 平移速度为 2\theta (弧度直接变距离) 对参数方程形式的向量作旋转和平移,然后对y坐标求极大值可以得到,极大值点对应的坐标: 从而可以用Geogebra绘制动态演示图片如下: rotation={{Cos[\[Theta]],

深入浅出理解目标检测的非极大值抑制(NMS)

一、参考资料物体检测中常用的几个概念迁移学习、IOU、NMS理解目标定位和检测系列（3）：交并比（IOU）和非极大值抑制（NMS）的python实现 Pytorch：目标检测网络-非极大值抑制(NMS) 二、非极大值抑制(NMS)相关介绍 1. NMS的概念非极大抑制(non maximum suppression, NMS)，顾名思义就是抑制不是极大值的元素，搜索局部的极大值。

【Python 数据分析】描述性统计：平均数（均值）、方差、标准差、极大值、极小值、中位数、百分位数、用箱型图表示分位数

目录简述 / 前言1. 平均数（均值）、方差、标准差、极大值、极小值2. 中位数3. 百分位数4. 用箱型图表示分位数简述 / 前言前面讲了数据分析中的第一步：数据预处理，下面就是数据分析的其中一个重头戏：描述性统计，具体内容为：平均数（均值）、方差、标准差、极大值、极小值、中位数、百分位数、用箱型图表示分位数。 1. 平均数（均值）、方差、标准差、极大值、极小值关键

面试题-手撕NMS(非极大值抑制)

非极大值抑制（Non-Maximum Suppression，NMS）是一种常用于目标检测和计算机视觉中的算法，用于去除重叠的边界框，保留最可能是真实目标的边界框。其核心就是对一组检测框，找出其中属于同一个类别且分数最高的那个框，然后把和这个框的IOU值大于阈值的那些框都删掉。在NMS中，其实用到了计算IOU的方法，可以参考：面试题-手撕IOU计算下面是代码： #include <i

收藏！攻克目标检测难点秘籍二，非极大值抑制与回归损失优化之路

点击上方“AI算法修炼营”，选择加星标或“置顶” 标题以下，全是干货前面的话在前面的秘籍一中，我们主要关注了模型加速之轻量化网络，对目标检测模型的实时性难点进行了攻克。但是要想获得较好的检测性能，检测算法的细节处理也极为重要。在众多的细节处理中，先来介绍非极大值抑制、回归损失函数这2个问题。本文主要介绍秘籍二：非极大值抑制与回归损失的优化之路。秘籍二. 非极大值抑制与回归损失优化之路当

收藏！攻克目标检测难点秘籍二，非极大值抑制与回归损失优化之路

点击上方“AI算法修炼营”，选择加星标或“置顶” 标题以下，全是干货前面的话在前面的秘籍一中，我们主要关注了模型加速之轻量化网络，对目标检测模型的实时性难点进行了攻克。但是要想获得较好的检测性能，检测算法的细节处理也极为重要。在众多的细节处理中，先来介绍非极大值抑制、回归损失函数这2个问题。本文主要介绍秘籍二：非极大值抑制与回归损失的优化之路。秘籍二. 非极大值抑制与回归损失优化之路当

利用离散序列的差分运算寻找序列的下降沿、上升沿、极大值(波峰)、极小值(波谷)的原理

我们先来看一看对于连续函数，我们通常是怎么求其极值的。通常我们用函数极值的第一充分条件和第二充分条件来求函数的极值。函数极值的第一充分条件和第二充分条件的内容如下：（懒得自己写了，直接把高等数学书上的内容截图发上来吧，大家将就看吧！）在实际工程中，我们用得最多的是第二充分条件。说完了连续函数求极值点，自然该说离散序列怎么找极值点了，即我们常说的寻找离散序列的波峰、波谷。为了说明

【目标检测】非极大值抑制NMS的原理与实现

非极大值抑制（Non-Maximum Suppression，NMS）是目标检测中常用的一种技术，它的主要作用是去除冗余和重叠过高的框，并保留最佳的几个。 NMS计算的具体步骤如下：首先根据目标检测模型输出结果，得到一系列候选框及其对应的概率分数。对所有候选框按照概率分数进行降序排序。选择概率最大的候选框并确定为预测框，同时删除所有与该预测框重叠度（IoU, Intersectio

极小极大值方法以及alpha-Beta剪枝

极小值极大值的适用条件：零和，完全信息假设有两个人在对弈，分别为Max和Min 所谓的极大极小，即Max要极大化自己的分数，而Min则要极小化Max的分数（注意棋局的分数是相对于Max而言）如下是极大极小的自下而上的推导过程蓝色线Min选择的分支，红色线为蓝色线选择的分支。上图得到的最终结果为Max应在0层选择右分支，得到的最低结果为-7 但是该方法存在一些无须访问的节点，因此

求矩阵的局部极大值（15 分）

求矩阵的局部极大值（15 分）给定M行N列的整数矩阵A，如果A的非边界元素A[i][j]大于相邻的上下左右4个元素，那么就称元素A[i][j]是矩阵的局部极大值。本题要求给定矩阵的全部局部极大值及其所在的位置。输入格式：输入在第一行中给出矩阵A的行数M和列数N（3≤M,N≤20）；最后M行，每行给出A在该行的N个元素的值。数字间以空格分隔。输出格式：每行按照“元素值行号列

数学用导数来求极大值和极小值

用导数来求极大值和极小值函数在哪里最高或最低？微积分可以帮助你！一个顺滑改变的函数的低点（级小值）或高点（极大值）是在其变成平坦的地方：（但不是所有平坦的地方都是极大值或极小值，也可以有个鞍点) 在哪里变成平坦？在坡度等于零的地方。坡度在哪里等于零？导数可以告诉我们！（你也许想先去阅读关于导数的内容。）例子：向上抛一个球。在球离开手 t 秒后，它

遗传算法求解函数极大值问题（附测试代码）

遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。简而言之，遗传算法就是通过每次选择比较好的个体进入下一次循环来保证每一轮解的最优特性，其核心思想有以下几个方面。（1）初始化值（染色体），转化成二进制的形式（为了方便交叉和变异）（2）使用轮盘赌算法设计策略来选择下一轮进入循环

目标检测锚框，NMS极大值抑制

目标检测锚框和NMS极大值抑制锚框NMS极大值抑制讲解锚框NMS 锚框NMS极大值抑制讲解锚框和NMS极大值抑制想必大家在诸多地方都遇到过，那么究竟什么是极大值抑制呢? 锚框锚框也就是我们很多书中说的anchor。这是什么意思呢？实际上这就是在进行目标检测的时候在特征图上每个点都设置相同数量的框框这就叫锚框。如图所示，我们可以看到左边的一堆方格子其实是特征层的像素