遗传算法求解函数极大值问题（附测试代码）

本文主要是介绍遗传算法求解函数极大值问题（附测试代码），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。
简而言之，遗传算法就是通过每次选择比较好的个体进入下一次循环来保证每一轮解的最优特性，其核心思想有以下几个方面。
（1）初始化值（染色体），转化成二进制的形式（为了方便交叉和变异）
（2）使用轮盘赌算法设计策略来选择下一轮进入循环的染色体（只要是为了防止当前适应度值不太好的染色体直接被淘汰）
（3）复制染色体（保证每一轮染色体的条数和初始染色体条数一样，比如初始染色体有4条，通过轮盘赌算法后只选择了3条，那么剩下的一条一般是复制当前轮中比较好的染色体，当然，这个时候4条染色体中有2条是一样的，所以要进行交叉和变异）
（4）交叉，交叉的策略很多，可以选择任意两条染色体相交叉（其实就是交换染色体对应的二进制的某些值，比如选择第一条染色体对应的二进制前3个值和第二条染色体对应的二进制前3个值对换，交叉的目的在于检验这些比较好的染色体相互组合后是否能达到求解要求，也可以说是保留最优染色体基因，其实交叉后也有可能会变差）
（5）变异，当染色体相互交叉后并不能找到最优值，就需要变异，变异就是改变某条染色体中对应的基因值，把染色体对应的二进制中某个1变成0，或者0变成1，变异策略也有很多，需要几个基因变异因问题不同而不同。
交叉和变异都是为了防止进入局部最优。
为了方便说明，根据遗传算法原理，求解二次函数极大值问题,定义域为（1,10）
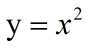
在这里插入图片描述
步骤为：
（1）根据定义域，初始化染色体数目和值
（2）计算每条染色体对应的y值
（3）根据轮盘赌算法选择下一次要遗传的染色体，染色体数目不够就复制
（4）二进制编码染色体
（5）交叉
（6）变异，更新下一轮循环染色体
（7）没有达到最大循环次数，返回（2），否则，输入目标值。
另外，交叉和变异后最好都检验下新的染色体是否还在定义域范围，如果超出范围，要调整。
代码如下：

clc;
clear all;
%遗传算法求y=x1^2在区间[1 10]的最大值，求y的值和x的值
%初始种群规模M=4
%终止迭代次数
%交叉概率
%变异概率
% 复制 、交叉、变异
beginNum=1+(10-1)*rand(1,4)%随机生成4个初始值，染色体
%计算初始使用度值
T=100;%最大循环次数
tt=1;
maxsyd=[];
while tt<=TbeginNumzydz=[];for j=1:length(beginNum)zydz(j)=beginNum(j)^2;end%      if max(zydz)==100
%          beginNum;
%          break;
%      end%根据轮盘赌算法决定下次遗传的%计算适应度的选择概率p=[];for z=1:length(zydz)p(z)=zydz(z)/sum(zydz);endp;%计算累加概率qq=[];q(1)=p(1);for y=2:length(p)q(y)=p(y)+ q(y-1);endq;gxnum=[];r=rand(1,length(beginNum));%在[0 1]之间产生随机数字r产生length(beginNum)个for k=1:length(r)if r(k)<=q(1)gxnum=[gxnum beginNum(1)];endfor kk=2:length(q) %每个随机数字r在q中的范围if q(kk-1)<r(k)&&r(k)<=q(kk)gxnum=[gxnum beginNum(kk)];endendendgxnum=unique(gxnum,'stable');%判断是否需要复制if length(gxnum)<length(beginNum)% 选择复制优势染色体while length(gxnum)~=length(beginNum)gxnum=[gxnum max(beginNum)];endendm=8;newbeginenum={};%转换成二进制后的初始数，方便变异和交叉操作for i=1:length(gxnum)n=beginNum(i);a=dec2bin(n*2^m);%     b=[a(1:end-m),'.',a(end-m+1:end)];% str2double(a)newbeginenum{i}=a;endt=char(newbeginenum(1));%转成字符串类型%所有二进制的位数必须一样，不足的在前面补0yycount=0;for yy=1:length(newbeginenum)% 找最长位数的二进制yyt1=length(char(newbeginenum(yy)));if yyt1>yycountyycount=yyt1;endendfor pj=1:length(newbeginenum)yy2=length(char(newbeginenum(pj)));if yy2<yycounttempj(1:yycount-yy2)='0';newbeginenum{pj}=strcat(tempj,char(newbeginenum(pj)));%更新newbeginenumendendnm=2;%交换前2位jcnewbeginenum={};%交叉产生新的染色体jcnewbeginenumfor nk=1:2:length(newbeginenum)-1t1=char(newbeginenum(nk));t2=char(newbeginenum(nk+1));tz1=t1(1:nm);tz2=t2(1:nm);% 交换tztemp=tz1;t1(1:nm)=tz2;t2(1:nm)=tztemp;jcnewbeginenum{nk}=t1;jcnewbeginenum{nk+1}=t2;end%判断变异是否超出定义域范围jcnewbeginenum(3);%% 变异，根据要求，设置变异概率10%，%变异基因个数jycountbyhbegine={}; %变异后的值，等下记得判断是否超出定义域的范围for jyk=1:length(jcnewbeginenum)jycount=ceil(length(char(jcnewbeginenum(jyk)))*0.1);% rk=randperm(length(char(jcnewbeginenumjyk))),jycount));%产生变异基因的位置rk=randperm(length(char(jcnewbeginenum(jyk))),jycount);% 替换变异位置bywz=char(jcnewbeginenum(jyk));for byw=1:length(rk)if strcmp(bywz(rk(byw)),'0')bywz(rk(byw))='1';elsebywz(rk(byw))='1';end%     bywz(rk(byw))=~bywz(rk(byw));endbyhbegine{jyk}=bywz;end%把变异后的值转换成十进制替换初始值zzbyhbegine=[];for ncs=1:length(byhbegine)tempaa=char(byhbegine(ncs));%二进制转换成十进制zzbyhbegine(ncs)=bin2dec(tempaa(1:end-m))+bin2dec(tempaa(end-m+1:end))/2^m;endbeginNum=zzbyhbegine;for bj=1:length(beginNum)if beginNum(bj)<1beginNum(bj)=1;endif beginNum(bj)>10beginNum(bj)=10;endendtt=tt+1;maxsyd=[maxsyd max(zydz)];
end
xsyd=1:100;
plot(xsyd,maxsyd,'r-')

运行结果
在这里插入图片描述
可以看到，在定义域为（1,10）中，遗传算法收敛速度还是非常快的（大约在第三轮就已经收敛了）。另外，在实验过程中，由于变异和交叉策略选择的原因，发现该算法还是会陷入局部最优，其陷入局部最优的概率为约为5%。