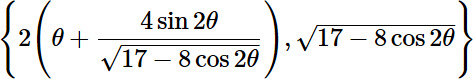原来椭圆在平移的同时绕型心旋转,极大值点的轨迹是漂亮的曲线

本文主要是介绍原来椭圆在平移的同时绕型心旋转,极大值点的轨迹是漂亮的曲线，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

下图所用的参数; 

椭圆标准情况下参数方程用 ( 5 cos(t), 3 sin(t) )

假设的旋转角速度为 \theta, 平移速度为 2\theta (弧度直接变距离)

对参数方程形式的向量作旋转和平移,然后对y坐标求极大值可以得到,极大值点对应的坐标:

从而可以用Geogebra绘制动态演示图片如下:

rotation={{Cos[\[Theta]],-Sin[\[Theta]]},{Sin[\[Theta]],Cos[\[Theta]]}};a=5;b=3;ellipse={{a Cos[t]},{b Sin[t]}};
movingEllipse=rotation.ellipse+{{2 \[Theta]},{0}}
sol=(Solve[{D[3 Cos[\[Theta]] Sin[t]+5 Cos[t] Sin[\[Theta]],t]==0/.{Cos[t]->x,Sin[t]->y},x^2+y^2==1},{x,y}]//FullSimplify)[[2]]
curve=(movingEllipse/.{Cos[t]->(5 Sin[\[Theta]])/Sqrt[17-8 Cos[2 \[Theta]]],Sin[t]->(3 Cos[\[Theta]])/Sqrt[17-8 Cos[2 \[Theta]]]}//FullSimplify)/.{\[Theta]->t}
list=Table[Manipulate[Show[ParametricPlot[{2 \[Theta]+5 Cos[t] Cos[\[Theta]]-3 Sin[t] Sin[\[Theta]],3 Cos[\[Theta]] Sin[t]+5 Cos[t] Sin[\[Theta]]},{t,0,2Pi},PlotRange->{{-6.2,60},{-6,6}}],
ParametricPlot[curve[[All,1]],{t,-Pi/2,\[Theta]},PlotStyle->Red,PlotRange->{{-6.2,20},{-6,6}}],ImageSize->Full],{{\[Theta],k},-Pi/2+0.01,9Pi}],{k,-(\[Pi]/2)+0.01`,9 \[Pi],1/49 (9.5` \[Pi]-0.01`)}];
Export["testEllipse.gif",list,"TransparentColor"->White,"TransitionEffect"->Background]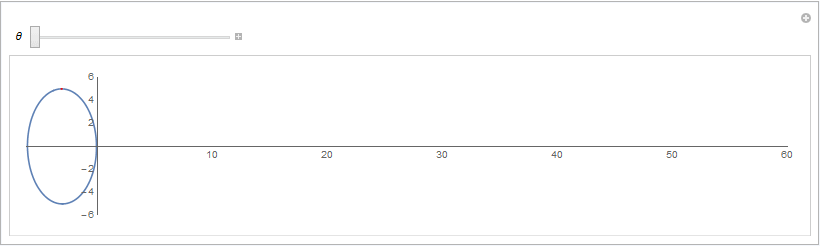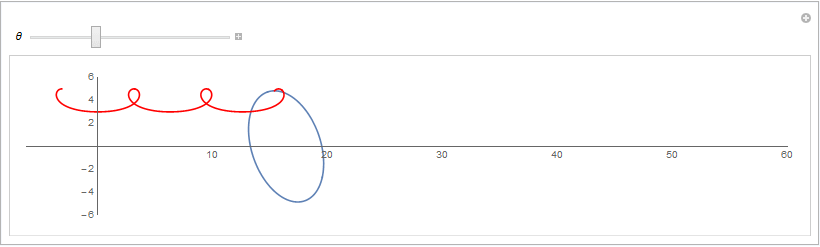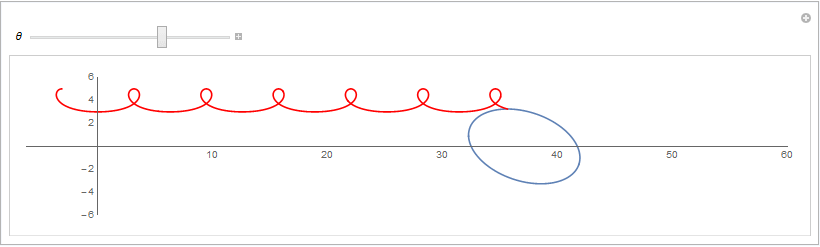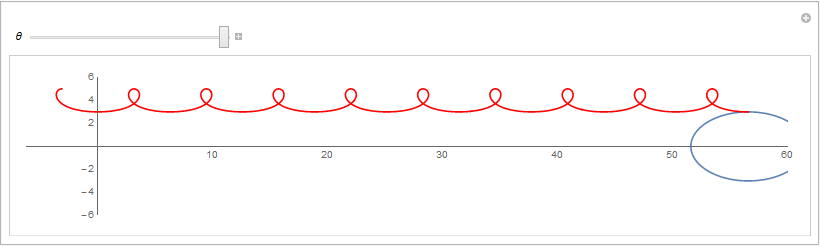

这篇关于原来椭圆在平移的同时绕型心旋转,极大值点的轨迹是漂亮的曲线的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---