文法专题
通过C语言将文法转化为语言
最近在学习编译原理,在做一道题时,突然产生想法,想通过C语言将文法产生的语言表现出来。 题目如下: 给定文法:S::=aB|bA A::=aS|bAA|a B::=bS|aBB|b 该文法所产生的语言是什么? 程序如下,可以注意相关的程序注解 #include<stdio.h> #in
【PL理论深化】(2) 语法分析 (Syntax) | 编程语言的语法结构:文法 | 语义结构 (Sematics)
💬 写在前面:编程语言是由归纳法生成的程序的集合。定义属于该语言的程序的形式的规则,即编写程序的规则,称为编程语言的 语法分析 (syntax) 而定义属于该语言的程序的意义的规则称为 语义结构(semantics)。这两者都是归纳定义的。 目录 0x00 语法分析(syntax analysis) 0x01 编程语言的语法结构:文法(grammar) 0x02 语义结构(Seman
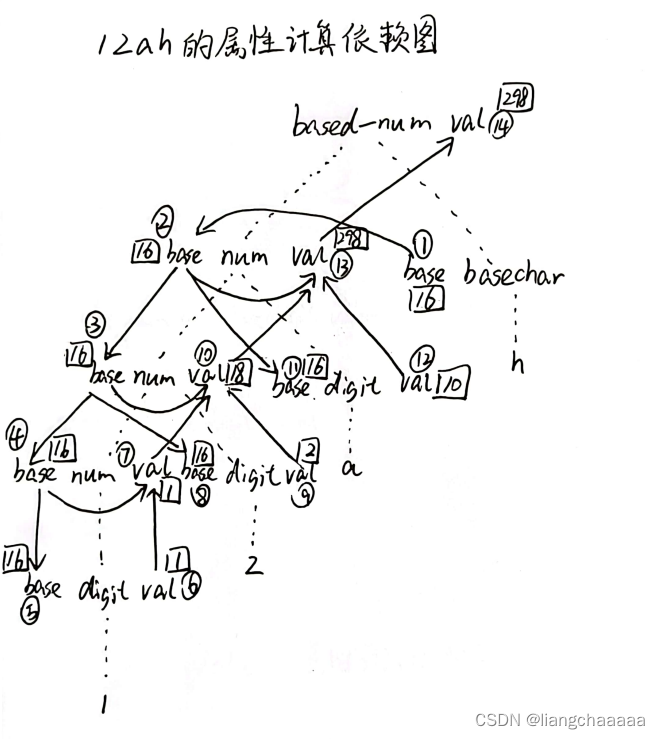
语法制导的翻译和属性文法
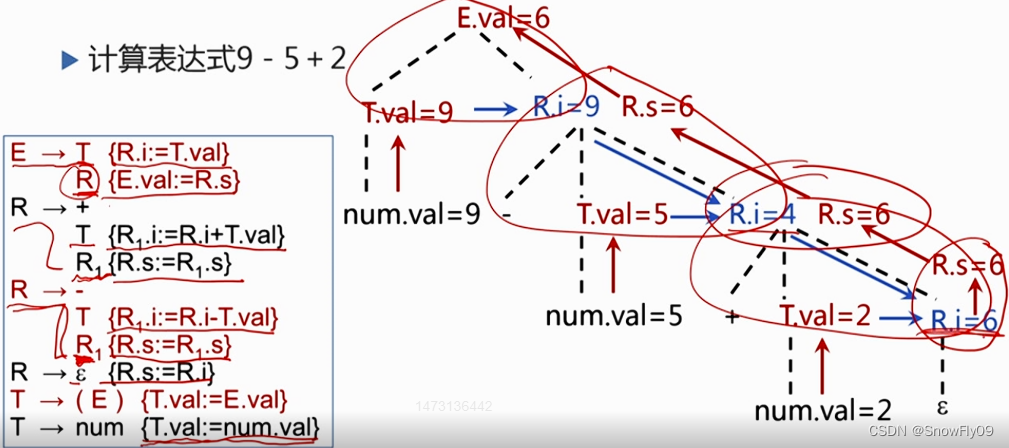
属性的分类 1.综合属性 重写规则(产生式)左部符号的属性是综合属性。一个结点相应文法符号的属性值通过语法分析树中它的子节点的属性之值计算(自底向上) 2.继承属性 出现在重写规则右部的符号的属性。一个结点相应文法符号的属性之值,通过语法树中它的兄弟节点与父节点相应文法符号的属性值来计算(自顶向下) 3.内在属性 不会出现在属性定义性出现集合中的属性。一般为终结符的属性。
编译原理实验4——LL(1)文法分析
本来是打算再写一个select集生成器的,但是时间有限再加上懒后来还是放弃了= =。 这个代码也是需要先新建一个文本文件sy4.in 文本文件中第一行有一个整数x,代表有x个产生式 接下来x行每行有三个字符串,分别代表产生式左边,右边还有对应的select集 最后一行还有一个字母s,代表起始字符 在读入了数据之后,若文法是LL(1)文法,则会输出"The Data is ok!" 否则
自顶向下语法分析方法:LL(1)文法的判别
例子:文法G[S]为 S->AB|bC A->ε|b B->ε|aD C->AD|b D->aS|c 第一步,求出能推出ε的非终结符 首先建立一个以文法的非终结符为上界的一维数组,其数组元素为非终结符,对应每一非终结符有一个标志位,用以记录能否推出ε。如下表 非终结符SABCD初值未定未定未定未定未定第1次扫描是是否第2次扫描是否 能否推出ε步骤如下: 第二步,计算FIR
【编译原理复习笔记】属性文法
属性文法 也称为属性翻译文法,由 Knuth 提出,以上下文无关文法为基础 (1)为每个文法符号(终结符与非终结符)配备相关的属性,代表与该文法符号相关的信息 (2)属性文法对于每个产生式都配备了对应的语义规则,标明了语义关系的传递 属性的分类 综合属性 自下而上的传递信息,根据产生式右部的符号属性计算左部被定义符号的综合属性 在语法树中,即根据子节点的属性和自身的自身属性来计算父节点的
7文法分析 软设刷题 软考 +
文法分析 刷题1-55-1010-1515-2020-2525-3030-3535-4040-45 知识点1-55-1010-1515-2020-2525-3030-35 刷题 1-5 1 沟通渠道公式如下:M=n*(n-1)/ 2。M表示沟通渠道数,n表示项目中的成员数 2 本题给出的NFA,能够识别字符串000,010等,以这两个字符串为例进行分析。 与之等价的DFA,
第3章 文法和语言(四)
七、句型的分析 句型分析就是识别一个符号串是否为某文法的句型,是某个推导的构造过程。在语言的编译实现中,把完成句型分析的程序称为分析程序或识别程序。分析算法又称识别算法。从左到右的分析算法,即总是从左到右地识别输入符号串,首先识别符号串中的最左符号,进而依次识别右边的一个符号。 1、自上而下的语法分析:从文法的开始符号出发,反复使用各种产生式,寻找与输入符号串匹配的推导。 例
第3章 文法和语言(三)
五、文法的类型 (1)0型文法(短语文法):对任一产生式α→β,都有α∈(VN∪VT)+, β∈(VN∪VT)* (2)1型文法(上下文有关文法): 对任一产生式α→β,都有|β|≥|α|, 仅仅 S→ε除外。即α1Aα2→α1βα2(A在VN中,其他在V*中,β≠ε) (3)2型文法(上下文无关文法): 对任一产生式α→β,都有α∈VN , β∈(VN∪VT)* 即A
第3章 文法和语言(二)
四、文法和语言的形式定义 1、文法的形式定义 1)规则(重写规则、产生式或生成式):是一个有序对(α,β)。记为α→β或 α∷=β,其中α∈V+,β∈V* 。 α称为规则的左部(或生成式的左部)。 β称为规则的右部(或生成式的右部)。 2)文法G[S]:文法为四元组(VN,VT,P,S) VN :非终结符集 VT :终结符集 P:产
第3章 文法和语言(一)
一、语言 语言是由句子组成的集合,是由一组记号所构成的集合。汉语--所有符合汉语语法的句子的全体英语--所有符合英语语法的句子的全体程序设计语言--所有该语言的程序的全体 二、文法 概念: 一种语言描述工具,用来定义句子的结构,用有限的规则把语言的全部句子描述出来,是以有穷的集合刻划无穷的集合的工具。 〈句子〉::=〈主语
C语言之Chomsky文法类型判断
文法G[S] = {VN,VT,P,S}: 其中VN(非终结符),VT(终结符),P(产生式集),是非空的有限集; S属于VN,是文法的开始符号; 根据产生式集来判断文法的类型: #include<stdio.h>#include<string.h>#define len 3//0型文法:左侧必须含有非终结符int zeroJudge(char part[2][10]
编译原理)判断文法的类型
实验内容 从文件中读取数据,判断其为0型文法、1型文法、2型文法还是3型文法,并指出其非终结集符、终结符集和开始符号。 java实现 package com.wang;import java.io.BufferedReader;import java.io.File;import java.io.FileNotFoundException;import java.io.FileRea
全量知识系统问题及SmartChat给出的答复 之14 解析器+DDD+文法型 之2
Q36. 知识系统中设计的三种文法解析器和设计模式之间的关系 进一步,我想将 知识系统中设计的三种语言(形式语言、人工语言和自然)的文法解析器和DDD中的三种程序类型(领域模型、领域实体和领域服务) 形式语言文法 我认为,DDD中的领域模型、领域实体和领域服务概念可以对应程序设计模式按目的(即完成什么样任务)划分的三种类型:创建型、结构型和行为型。并且是作为任务的目的来设计的。 以下是对对
全量知识系统问题及SmartChat给出的答复 之13 解析器+DDD+文法型
Q32. DDD的领域概念和知识系统中设计的解析器之间的关系。 那下面,我们回到前面的问题上来。 前面说到了三种语法解析器,分别是 形式语言的(机器或计算机语言)、人工语言的和自然语言的。再前面,我们聊到了DDD设计思想,提到了领域模型、领域实体和领域服务。 问题: DDD中的这些概念,和这些语法解析器之间有什么关系?是否能将二者对应起来或者关联或者联系起来呢?如果能,就应该可以将两方面的程
全量知识系统问题及SmartChat给出的答复 之13 解析器+DDD+文法型 之2
Q36. 知识系统中设计的三种文法解析器和设计模式之间的关系 进一步,我想将 知识系统中设计的三种语言(形式语言、人工语言和自然)的文法解析器和DDD中的三种程序类型(领域模型、领域实体和领域服务) 形式语言文法 我认为,DDD中的领域模型、领域实体和领域服务概念可以对应程序设计模式按目的(即完成什么样任务)划分的三种类型:创建型、结构型和行为型。并且是作为任务的目的来设计的。 以下是对对
【学习笔记】自动机理论、语言和计算导论(五:上下文无关文法和上下文无关语言)
Content 上下文无关文法语法分析树上下文无关文法的应用文法和语言的歧义性 上下文无关文法 语言的文法性描述包括四个重要部分∶ 一个符号的有穷集合,它构成了被定义语言的串。这个字母表称为终结符或终结符号。一个变元的有穷集合,变元有时也称为非终结符或语法范畴。每个变元代表一个语言,即一个串的集合。有一个变元称为初始符号,它代表语言开始被定义的地方。其他变元代表其他辅助的字符串
正规文法、正规式、确定的有穷自动机DFA、不确定的有穷自动机NFA 的概念、区分以及等价性转换【我直接拿下!】
文章目录 正规文法正规式有穷自动机确定的有穷自动机——DFA不确定的有穷自动机——NFADFA 与 NFA 的区分 正规式转换为正规文法正规文法转换为正规式NFA 转换为 DFANFA 最小化 NFA 转换为正规式正规式转换为 NFA正规文法转换为 NFANFA 转换为正规文法 前言: 在学习正规文法之前,需要先了解一下什么是文法,具体可以查看这篇文章,总结的比较好 —— 编
根据文法求对应的语言
技巧:最后得到的是终结符组成的闭包 例题: 文法G[S]: S-->AB A-->aAb|ab B-->Bc|,求对应的语言 ①S-->(aAb|ab)(Bc|) ②我们可以观察到,无论A-->aAb还是A-->ab,都一定会同时出现ab,但是B-->Bc,会推出终结符c,B-->,则不会推出c,所以c可以取到0,a和b一定会出现。 ③最后得到结果:
将正规文法转化为正规式
将正规文法转化为正规式有以下几个规则: 通过一道例题来讲解: ①A-->aC|bA ②C-->bD ③D-->aC|bD| (1)首先将②带入③(不能将自身带入自身例如D-->aC|bD|,文法中带D,不能带入D) D=abD|bD|=(ab|b)D | ,所以对应规则2(A-->xA|y),其中"(ab|b)"对应的是x,y对应的是 所以④D=x*y=(ab|b)*=(ab|b
语法树的画法(根据文法求字符串)
目录 1.语法树的画法 2.语法树的短语 3.直接短语(直接到根部) 4.素短语 5.句柄 6.算符优先分析句型 1.语法树的画法 文法G[E]:E->E+E | E*E | (E) | i ,字符串 i+i*i 推导方式有两种最左推导和最右推导(推导的技巧就是逐步靠近字符串的形式) 最左推导(从左往右替换): E->E+E->i+E->i+E*E->i+i*E->i
【计算理论】【《计算理论导引(原书第3版)》笔记】第二章:上下文无关文法
文章目录 @[toc]2.1|上下文无关文法概述上下文无关文法的形式化定义乔姆斯基范式定理证明 个人主页:丷从心 系列专栏:计算理论 2.1|上下文无关文法概述 上下文无关文法的形式化定义 上下文无关文法是一个 4 4 4元组 ( V , Σ , R , S ) (V , \Sigma , R , S) (V,Σ,R,S),且 V V V是一个有穷集合,称为
NLP+句法结构(三)︱中文句法结构(CIPS2016、依存句法、文法)
摘录自:CIPS2016 中文信息处理报告《第一章 词法和句法分析研究进展、现状及趋势》P8 -P11 CIPS2016> 中文信息处理报告下载链接:http://cips-upload.bj.bcebos.com/cips2016.pdf . NLP词法、句法、语义、语篇综合系列: NLP+词法系列(一)︱中文分词技术小结、几大分词引擎的介绍与比较 NLP+词法系列(二)︱中
文法俱乐部 第三章 动词时态
简单式 简单式的动词可以清楚交代此动作是发生于哪个时段。而与它搭配的时间副词通常会明确标示出一个时段。也就是说:简单式的时间是括弧的形状,我们可以用括弧把简单式的时间括起来。在以下的叙述中,我们就以括弧来表示简单式中所描述的时间,这个括弧大小不拘,可以小到一个点,也可以大到无限,可是必须标示得很明确。现在来看看几个例子,请注意观察动词时态与时间副词之间的关系: 一、过去时间