本文主要是介绍第3章 文法和语言(四),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
七、句型的分析
- 句型分析就是识别一个符号串是否为某文法的句型,是某个推导的构造过程。
- 在语言的编译实现中,把完成句型分析的程序称为分析程序或识别程序。分析算法又称识别算法。
- 从左到右的分析算法,即总是从左到右地识别输入符号串,首先识别符号串中的最左符号,进而依次识别右边的一个符号。
1、自上而下的语法分析:从文法的开始符号出发,反复使用各种产生式,寻找与输入符号串匹配的推导。
例:文法G:S → cAd A → ab A → a 识别输入串 w = cabd 是否该文法的句子
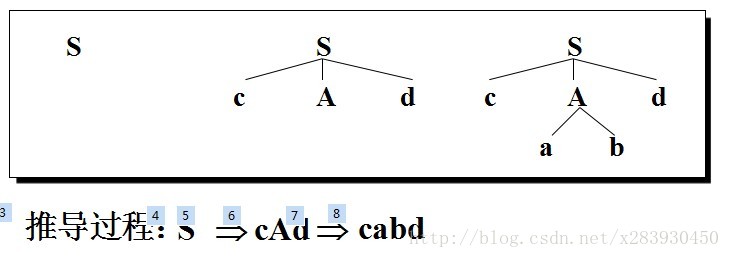

2、自下而上的语法分析:从输入符号串开始,逐步进行归约,直至归约到文法的开始符号。
例:文法G:S → cAd A → ab A → a 识别输入串 w = cabd 是否该文法的句子
例:文法G:S → cAd A → ab A → a 识别输入串 w = cabd 是否该文法的句子

3、句型分析的有关问题
1)如何选择使用哪个产生式进行推导?
假定要被代换的最左非终结符号是V,且有n条规则:V→A1|A2|…|An,那么如何确定用哪个右部去替代V?
2)如何识别可归约的串?
在自下而上的分析方法中,在分析程序工作的每一步,都是从当前串中选择一个子串,将它归约到某个非终结符号,该子串称为“可归约串”(“句柄”)
4、短语、直接短语、句柄的定义:
文法G[S],αβδ是G的一个句型,如果:
S=*>αAδ且A=+>β
则称β是句型αβδ相对于非终结符A的短语。
若有A=>β则称β是句型αβδ相对于规则A→β的直接短语(或简单短语)。
一个句型的最左直接短语称为该句型的句柄。
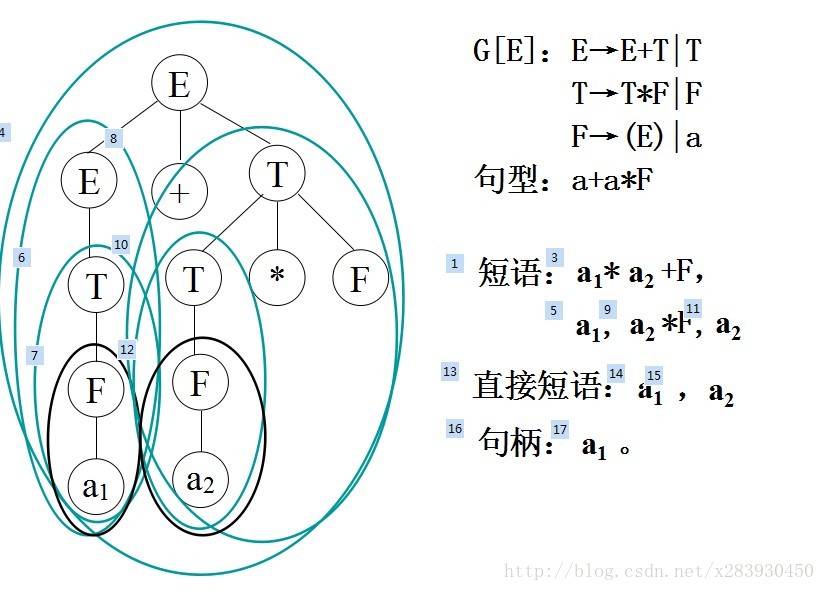
如何用语法树理解短语?
1、语法树中一棵子树的所有叶子从左向右排列起来形成一个相对于子树根的短语。
2、只有父子两代的子树的叶子从左向右排列起来构成的短语称为直接短语。
3、最左直接短语称为句柄。
1)如何选择使用哪个产生式进行推导?
假定要被代换的最左非终结符号是V,且有n条规则:V→A1|A2|…|An,那么如何确定用哪个右部去替代V?
2)如何识别可归约的串?
在自下而上的分析方法中,在分析程序工作的每一步,都是从当前串中选择一个子串,将它归约到某个非终结符号,该子串称为“可归约串”(“句柄”)
4、短语、直接短语、句柄的定义:
文法G[S],αβδ是G的一个句型,如果:
S=*>αAδ且A=+>β
则称β是句型αβδ相对于非终结符A的短语。
若有A=>β则称β是句型αβδ相对于规则A→β的直接短语(或简单短语)。
一个句型的最左直接短语称为该句型的句柄。
如何用语法树理解短语?
1、语法树中一棵子树的所有叶子从左向右排列起来形成一个相对于子树根的短语。
2、只有父子两代的子树的叶子从左向右排列起来构成的短语称为直接短语。
3、最左直接短语称为句柄。

八、有关文法实用中的一些说明
1、有关文法的实用限制
文法中不得含有有害规则和多余规则。
“有害规则”:形如U→U的产生式。会引起文法的二义性。
“多余规则”:指文法中任何句子的推导都不会用到的规则。
1)文法中某些非终结符不在任何规则的右部出现,该非终结符称为不可到达的。
2)文法中某些非终结符,由它不能推出终结符号串来,称为不可终止的。
文法中不得含有有害规则和多余规则。
“有害规则”:形如U→U的产生式。会引起文法的二义性。
“多余规则”:指文法中任何句子的推导都不会用到的规则。
1)文法中某些非终结符不在任何规则的右部出现,该非终结符称为不可到达的。
2)文法中某些非终结符,由它不能推出终结符号串来,称为不可终止的。

2、上下文无关文法中的ε规则
- 具有形式A→ε的规则称为ε规则,其中A∈VN
- 某些著作和讲义中限制这种规则的出现。因为ε规则会使有关文法的一些讨论和证明变得复杂
- 两种定义的唯一差别是ε句子在不在语言中。
这篇关于第3章 文法和语言(四)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





