本文主要是介绍【学习笔记】自动机理论、语言和计算导论(五:上下文无关文法和上下文无关语言),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Content
- 上下文无关文法
- 语法分析树
- 上下文无关文法的应用
- 文法和语言的歧义性
上下文无关文法
语言的文法性描述包括四个重要部分∶
- 一个符号的有穷集合,它构成了被定义语言的串。这个字母表称为终结符或终结符号。
- 一个变元的有穷集合,变元有时也称为非终结符或语法范畴。每个变元代表一个语言,即一个串的集合。
- 有一个变元称为初始符号,它代表语言开始被定义的地方。其他变元代表其他辅助的字符串类,这些变元被用来帮助初始符号定义该语言。
- 一个产生式(或者规则)的有穷集合,它用来表示语言的递归定义。每个产生式包括∶
(a)一个变元,它被该产生式定义或者部分定义,这个变元通常称为产生式的头。
(b)一个产生式符号→。
(c)一个包含零个或多个终结符号或变元的串,它叫作产生式的体,表示一种构成产生式
头变元的语言中的串的方法。具体的构造过程是∶ 保持终结符号不变,把任何已知属于该语言的串里出现的产生式的头用产生式的体替换。
此四个部分构成了一个上下文无关文法,简称文法或者CFG。一个CFG G G G可以用组成它的四部分表示,记作 G = ( V , T , P , S ) G=(V, T, P, S) G=(V,T,P,S),其中 V V V是变元(Variable)的集合, T T T是终结符号(Terminal)的集合, P P P是产生式(Production)的集合, S S S代表初始符号(Start symbol)。
例: { 0 , 1 } \{0, 1\} {0,1}上的回文的文法 G p a l = ( { P } , { 0 , 1 } , A , P ) G_{pal}=(\{P\}, \{0, 1\}, A, P) Gpal=({P},{0,1},A,P),其中 A A A如下
1. P → ε 2. P → 0 3. P → 1 4. P → 0 P 0 5. P → 1 P 1 1.\quad P \to \varepsilon\quad2.\quad P \to 0\quad3.\quad P\to 1\quad 4.\quad P\to 0P0 \quad 5.\quad P\to 1P1 1.P→ε2.P→03.P→14.P→0P05.P→1P1
产生式简便记号 P → ε ∣ 0 ∣ 1 ∣ 0 P 0 ∣ 1 P 1 P\to\varepsilon | 0 | 1 | 0P0 | 1P1 P→ε∣0∣1∣0P0∣1P1
推断一个特定的串确实在一个特定的语言的变元中:递归推理,推导。
递归推理:从产生式的体到产生式的头来使用规则。也就是说,对于产生式的体中的变元,可以取出一个已知属于这个变元所代表的语言的串,然后把得到的串按照正确的顺序与体中出现的终结符号连接起来,并且推断出得到的串在该产生式的头中的变元的语言中。
推导:从产生式的头到体来使用规则。具体的做法是∶使用以初始符号为头的一个产生式来扩展初始符号,接着通过替换体中变元的方式来扩展所得到的串,具体替换的方式是用一个以该变元为头的产生式的体来替换该变元。继续这个过程,直到得到的字符串中只有终结符。这个文法的语言就是所有能用这种方式得到的终结符串。
设 G = ( V , T , P , S ) G =(V, T, P, S) G=(V,T,P,S)是一个 CFG, α A β αAβ αAβ是一个包含终结符和变元的串,其中 A A A是一个变元,也就是说, a a a和 β β β都是 ( V ∪ T ) ∗ (V\cup T)^* (V∪T)∗中的串,而 A ∈ V A\in V A∈V。设 A → γ A→\gamma A→γ是 G G G的一个产生式,那么我们称 α A β ⇒ G a γ β αAβ\underset{G}{\Rightarrow} a\gammaβ αAβG⇒aγβ,简记做 α A β ⇒ a γ β αAβ\Rightarrow a\gammaβ αAβ⇒aγβ。注意,在推导的每一步中都可以替换串中任何位置的任何一个变元,只要用该变元的任何一个产生式的体替换该变元即可。可以推广到多步推导 ⇒ ∗ \overset{*}{\Rightarrow} ⇒∗。为限制推导规则,要求按最左或最右顺序进行替换,称为最左推导 ⇒ l m \underset{lm}{\Rightarrow} lm⇒和最右推导称为最左推导 ⇒ r m \underset{rm}{\Rightarrow} rm⇒。
例:表示正则表达式 ( a + b ) ( a + b + 0 + 1 ) ∗ \mathbf{(a+b)(a+b+0+1)^*} (a+b)(a+b+0+1)∗的文法 G = ( { E , I } , { + , ∗ , ( , ) , a , b , 0 , 1 } , P , E ) G=(\{E, I\}, \{+, *, (, ), a, b, 0, 1\}, P, E) G=({E,I},{+,∗,(,),a,b,0,1},P,E),其中 P P P代表产生式 E → I ∣ E + E ∣ E ∗ E ∣ ( E ) , I → a ∣ b ∣ I a ∣ I b ∣ I 0 ∣ I 1 E\to I|E+E|E*E|(E), I\to a|b|Ia|Ib|I0|I1 E→I∣E+E∣E∗E∣(E),I→a∣b∣Ia∣Ib∣I0∣I1
递归推理:
推导 E ⇒ ∗ a ∗ ( a + b 00 ) E\overset{*}{\Rightarrow}a*(a+b00) E⇒∗a∗(a+b00):(最左)
E ⇒ E ∗ E ⇒ I ∗ E ⇒ a ∗ E ⇒ a ∗ ( E ) ⇒ a ∗ ( E + E ) ⇒ a ∗ ( I + E ) ⇒ a ∗ ( a + E ) ⇒ a ∗ ( a + I ) ⇒ a ∗ ( a + I 0 ) ⇒ a ∗ ( a + I 00 ) ⇒ a ∗ ( a + b 00 ) E \Rightarrow E * E \Rightarrow I * E \Rightarrow a * E \Rightarrow a * ( E ) \Rightarrow a * ( E + E ) \Rightarrow a * ( I + E ) \\ \Rightarrow a * ( a + E ) \Rightarrow a * ( a + I ) \Rightarrow a * ( a + I 0 ) \Rightarrow a * ( a + I 00 ) \Rightarrow a * ( a + b 00 ) E⇒E∗E⇒I∗E⇒a∗E⇒a∗(E)⇒a∗(E+E)⇒a∗(I+E)⇒a∗(a+E)⇒a∗(a+I)⇒a∗(a+I0)⇒a∗(a+I00)⇒a∗(a+b00)
文法的语言 CFG G = ( V , T , P , S ) G=(V, T, P, S) G=(V,T,P,S)的语言 L ( G ) L(G) L(G)是指从初始符号推导出的所有终结符串的集合。 L ( G ) = { w ∈ T ∗ ∣ S ⇒ G ∗ w } L(G)=\{w\in T^*\ | \ S\overset{*}{\underset{_G}\Rightarrow}w\} L(G)={w∈T∗ ∣ SG⇒∗w}。如果 L L L是某个上下文无关文法的语言,则称为上下文无关语言或CFL。
句型 对CFG G = ( V , T , P , S ) G=(V, T, P, S) G=(V,T,P,S),任何满足 S ⇒ ∗ α S\overset{*}{\Rightarrow}\alpha S⇒∗α的串 α ∈ ( V ∪ T ) ∗ \alpha \in (V\cup T)^* α∈(V∪T)∗称为句型。如果满足 ⇒ l m ∗ α \overset{*}{\underset{lm}\Rightarrow}\alpha lm⇒∗α称为左句型,如果满足 ⇒ r m ∗ α \overset{*}{\underset{rm}\Rightarrow}\alpha rm⇒∗α称为右句型。 L ( G ) L(G) L(G)是由所有属于 T ∗ T^* T∗的句型组成的。
语法分析树
对于文法 G = ( V , T , P , S ) G=(V, T, P, S) G=(V,T,P,S)来说, G G G的语法分析树是满足下列条件的树∶
- 每个内部节点的标号是 V V V中的一个变元。
- 每个叶节点的标号可以是一个变元、一个终结符或者 ε ε ε。但是,如果叶节点的标号是 ε ε ε,那么它一定是其父节点惟一的子节点。
- 如果某个内部节点的标号是 A A A,并且它的子节点的标号从左到右分别为∶ X 1 , X 2 , … , X k X_1, X_2, \dots, X_k X1,X2,…,Xk,那么 A → X 1 X 2 … X k A→X_1X_2\dots X_k A→X1X2…Xk一定是 P P P中的一个产生式。注意;如果其中某个 X X X为 ε ε ε,那么 X X X一定是 A A A惟一的子节点,并且 A → ε A→ε A→ε是 G G G的一个产生式。


如果看到任意一棵语法分析树的所有叶子的标号,并按照从左到右的顺序将其连接起来,就可以得到一个串,这个串称作该树的产物,其实它总是根节点处的变元所能推导出来的串。特别重要的是有一些满足以下条件的语法分析树∶
1.它的产物是终结符串,即所有叶节点的标号都是终结符或者 ε ε ε。
2.根节点的标号是初始符号。
递归推理,推导(任意、最左或最右),语法分析树是等价的。证明略。
上下文无关文法的应用
语法分析器 用文法来描述编程语言。语法分析器是编译器的一部分,用来发现源程序的结构并把该结构表示称为语法分析树。
例:括号匹配。 G b a l = ( { B } , { ( , ) } , P , B ) G_{bal}=(\{B\}, \{(,)\}, P, B) Gbal=({B},{(,)},P,B),其中 P P P为产生式 B → B B ∣ ( B ) ∣ ε B \to BB|(B)|\varepsilon B→BB∣(B)∣ε。
语法分析器生成器YACC

标记语言
HTML文法:

XML文法 标记符DTD标准:
<!DOCTYPE DTD_name[ListOfElements<!ELEMENT Ele_name (DescribeOfElements)>
]>
元素的描述是正则表达式,包含其他元素的名字,和关键字#PCDATA表示不含标记符的任意文本。运算符有并( ∣ | ∣),连接(,),闭包(*表示零次及以上,+表示一次及以上,?表示零次或一次),括号。
例子:假设的计算机DTD标准。
文法和语言的歧义性
例子:句型 E + E ∗ E E+E*E E+E∗E,有两种推导
1. E ⇒ E + E ⇒ E + E ∗ E E\Rightarrow E+E\Rightarrow E+E*E E⇒E+E⇒E+E∗E
2. E ⇒ E ∗ E ⇒ E + E ∗ E E\Rightarrow E*E\Rightarrow E+E*E E⇒E∗E⇒E+E∗E
一个CFG G = ( V , T , P , S ) G=(V, T, P, S) G=(V,T,P,S)是歧义的,如果 T T T中至少存在一个串 w w w,对于 这个串可以找到两棵不同的语法分析树满足如下条件∶它们的根都是 S S S,产物都是 w w w。如果一个文法使得任意的串都最多只对应一棵语法分析树,那么该文法就是无歧义的。
消除歧义性的办法:
强制优先级:
是引入几个不同的变元,每个变元代表拥有同样级别的"黏结强度"的那些表达式。更明确的说就是∶
- 因子是不能被相邻的运算符(包括 ∗ * ∗和 + + +)打断的表达式,因此在我们的表达式文法中的因子只有:
(a)标识符——不可能通过增加运算符的方法来把一个标识符打断。
(b)任何被括号括起来的表达式——无论括号里面括的是什么。括号的用处正是用来防止
括号里面的内容成为括号外面的运算符的操作数。 - 项是不能被相邻的 + + +打断的表达式。在我们的例子中,只有 + + +和 ∗ * ∗是运算符,因此项就是
一个和几个因子的乘积。例如,项 a ∗ b a* b a∗b是可以被打断的,只要采用左结合的规则并且把 a 1 ∗ a1* a1∗放到它的左边,也就是说, a 1 + a ∗ b a1+a*b a1+a∗b被结合为 ( a 1 ∗ a ) ∗ b (a1* a)*b (a1∗a)∗b,因而 a ∗ b a*b a∗b被打断了。然而,仅仅在它的左边放置一个加号项(比如 a 1 + a1+ a1+)或在它的右边放置 + a 1 +a1 +a1是无法打断 a ∗ b a*b a∗b的, a 1 + a ∗ b a1+a*b a1+a∗b的正确结合是 a 1 + ( a ∗ b ) a1+(a*b) a1+(a∗b), a ∗ b + a 1 a*b+a1 a∗b+a1的正确结合是 ( a ∗ b ) + a 1 (a*b)+a1 (a∗b)+a1。 - 表达式是指任何可能的表达式,其中包括可以被相邻的 ∗ * ∗或 + + +打断的表达式。因此,例子中的表达式就是一个或多个项的和。

强制顺序:最左推导。无歧义的文法中,最左最右推导是唯一的。
固有歧义性
L = { a n b n c m d m ∣ n ≥ 1 , m ≥ 1 } ∪ { a n b m c m d n ∣ n ≥ 1 , m ≥ 1 } L = \{ a ^ { n } b ^ { n } c ^ { m } d ^ { m } | n \geq 1 , m \geq 1 \} \cup \{ a ^ { n } b ^ { m } c ^ { m } d ^ { n } | n \geq 1 , m \geq 1 \} L={anbncmdm∣n≥1,m≥1}∪{anbmcmdn∣n≥1,m≥1}
即, L L L包含所有满足下列条件的 a + b + c + d + \mathbf{a^+b^+c^+d^+} a+b+c+d+形式的串:
1. a a a和 b b b的个数一样且 c c c和 d d d的个数一样,或者2. a a a和 d d d的个数一样且 b b b和 c c c的个数一样。
L L L的一个文法:
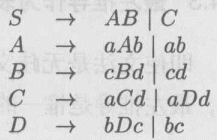
串 a a b b c c d d aabbccdd aabbccdd有两个最左推导:
- S ⇒ l m A B ⇒ l m a A b B ⇒ l m a a b b B ⇒ l m a a b b c B d ⇒ l m a a b b c c d d S\underset{lm}{\Rightarrow}AB\underset{lm}{\Rightarrow}aAbB\underset{lm}{\Rightarrow}aabbB\underset{lm}{\Rightarrow}aabbcBd\underset{lm}{\Rightarrow}aabbccdd Slm⇒ABlm⇒aAbBlm⇒aabbBlm⇒aabbcBdlm⇒aabbccdd
- S ⇒ l m C ⇒ l m a C d ⇒ l m a a D d d ⇒ l m a a b D c d d ⇒ l m a a b b c c d d S\underset{lm}{\Rightarrow}C\underset{lm}{\Rightarrow}aCd\underset{lm}{\Rightarrow}aaDdd\underset{lm}{\Rightarrow}aabDcdd\underset{lm}{\Rightarrow}aabbccdd Slm⇒Clm⇒aCdlm⇒aaDddlm⇒aabDcddlm⇒aabbccdd

这篇关于【学习笔记】自动机理论、语言和计算导论(五:上下文无关文法和上下文无关语言)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!











