本文主要是介绍【PL理论深化】(2) 语法分析 (Syntax) | 编程语言的语法结构:文法 | 语义结构 (Sematics),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

- 💬 写在前面:编程语言是由归纳法生成的程序的集合。定义属于该语言的程序的形式的规则,即编写程序的规则,称为编程语言的 语法分析 (syntax) 而定义属于该语言的程序的意义的规则称为 语义结构(semantics)。这两者都是归纳定义的。
目录
0x00 语法分析(syntax analysis)
0x01 编程语言的语法结构:文法(grammar)
0x02 语义结构(Semantics)
0x00 语法分析(syntax analysis)
下面是一个由整数和四则运算符所构成的整数表达式集合,即整数表达式语言。
比如,以下整数表达式属于该语言中的程序:
![]()
.
像上述那样,程序通常用一维字符串来编写。
但实际上,计算机程序具有树形的二维结构,例如字符串:
![]()
我们将程序表示为树结构:
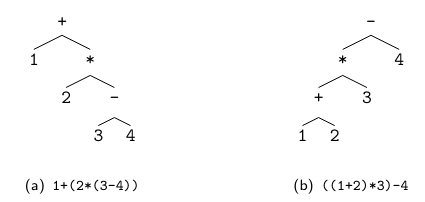
对应于图 (a) 的程序:
![]()
而对应于图 (b) 的程序,将用字符串编写的一维程序转换为二维树结构的技术 ——
称为 语法分析 (syntax analysis) 或 解析 (parsing) 。
(我们不会详细讨论语法结构分析的方法,而是着重于程序的结构如何呈现为树形)
0x01 编程语言的语法结构:文法(grammar)
假设程序的结构以树形结构明确给出,
整数表达式语言的语法结构可以通过以下推导规则归纳定义:
![]()
编程语言的语法结构通常采用 文法 (grammar) ,而不是推理规则来定义。
整数表达式语言的语法结构用文法表示如下:
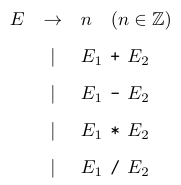
上述规则表示有 5 种方法可以生成整数表达式。
根据第一条规则,任意整数 () 都可以是一个整数表达式。
而其余的规则意味着,对于任意两个整数表达式 和
,
可以用四则运算符连接它们,从而创建一个新的整数表达式。
.
由于归纳规则的特性,通过这五种有限规则,可以生成无限多个任意的整数表达式。
例如,整数表达式 就是这样创建的:
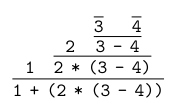
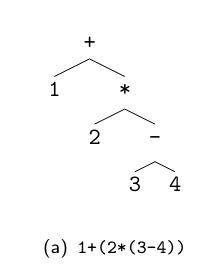
如果将证明树的上下颠倒,并强调树的结构,就得到了图 (A) 。
像这样通过归纳定义的编程语言的语法结构,具有生成二维程序的规则。
.
为了将二维结构清晰地写成一维形式,只需适当地使用括号,例如表达为 。
0x02 语义结构(Semantics)
如果语法结构是定义编程语言中程序外观的规则。
那么 语义结构 (semantics) 则是决定程序执行意义的规则。
程序的含义可以有多种定义,但对于整数表达式而言,
以计算表达式得到的整数值来定义其含义是最自然的。
我们可以这样表达:"计算整数表达式 得到整数
" 或者 "整数表达式
的含义是
"。
.
例如, 表示程序
的含义是等于 −1。
这里的 表示一个关于程序和整数之间的二元关系。
换言之,若将程序的集合表示为 ,整数的集合表示为
,
则 是
的一个子集 (即
),它定义了整数表达式的语义结构。
对于整数表达式,可以通过以下推理规则来定义集合 :
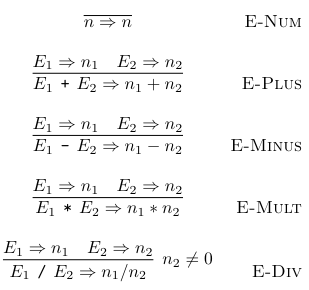
.
第一条规则 (E-Num) 对于任意整数 ,表示
是集合
的元素。
这里,整数 的意义被定义为整数值
。
第二条规则 (E-Plus) 表示如果 和
是
的元素,
则 也是
的元素,其余规则类似地定义。
.
然而,对于除法,定义限定 n2 不为零时才有意义。
例如,根据上述规则定义的集合 包含元素
。
整数表达式 的含义被定义为 3。
可以证明 是集合
的元素如下所示:
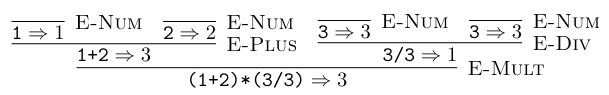
.
相对地,有些表达式可能看起来是正确的,但实际上可能没有定义。
例如,整数表达式 对于任何整数
,
都无法通过推理规则 进行证明。
.
因为整个表达式涉及除法,如果要证明它,就只能应用规则 。
但在这种情况下,由于分母计算结果为 0,因此无法应用 规则。
这说明,并非所有通过编程语言的语法结构定义的程序都具有执行的实际意义。
即使通过了编译器的语法分析阶段,仍可能存在无法正确执行的程序!
.
到目前为止,我们已经从定义推理规则的角度定义了语义结构,
但是也可以直接从程序执行规则的角度解释这些规则。
例如,规则 描述了计算表达式
的过程。
我们首先递归地计算表达式 和
的值,得到
和
,
然后定义为将这两个整数相加的过程。
通过这种方式解释语义结构,证明树的生成过程就成为程序执行的过程,
并且通过将语义结构定义为递归函数,我们可以直接获得编程语言的解释器 (interpreter) 。

📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2022.9.14
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 - R. Neapolitan, Foundations of Algorithms (5th ed.), Jones & Bartlett, 2015. - T. Cormen《算法导论》(第三版),麻省理工学院出版社,2009年。 - T. Roughgarden, Algorithms Illuminated, Part 1~3, Soundlikeyourself Publishing, 2018. - J. Kleinberg&E. Tardos, Algorithm Design, Addison Wesley, 2005. - R. Sedgewick&K. Wayne,《算法》(第四版),Addison-Wesley,2011 - S. Dasgupta,《算法》,McGraw-Hill教育出版社,2006。 - S. Baase&A. Van Gelder, Computer Algorithms: 设计与分析简介》,Addison Wesley,2000。 - E. Horowitz,《C语言中的数据结构基础》,计算机科学出版社,1993 - S. Skiena, The Algorithm Design Manual (2nd ed.), Springer, 2008. - A. Aho, J. Hopcroft, and J. Ullman, Design and Analysis of Algorithms, Addison-Wesley, 1974. - M. Weiss, Data Structure and Algorithm Analysis in C (2nd ed.), Pearson, 1997. - A. Levitin, Introduction to the Design and Analysis of Algorithms, Addison Wesley, 2003. - A. Aho, J. Hopcroft, and J. Ullman, Data Structures and Algorithms, Addison-Wesley, 1983. - E. Horowitz, S. Sahni and S. Rajasekaran, Computer Algorithms/C++, Computer Science Press, 1997. - R. Sedgewick, Algorithms in C: 第1-4部分(第三版),Addison-Wesley,1998 - R. Sedgewick,《C语言中的算法》。第5部分(第3版),Addison-Wesley,2002 |
这篇关于【PL理论深化】(2) 语法分析 (Syntax) | 编程语言的语法结构:文法 | 语义结构 (Sematics)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







