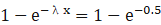指数分布专题

指数分布的两种形式

指数分布是连续概率分布的一种，常用于描述等待时间、寿命等随机变量的分布。 1. 标准形式的指数分布标准形式的指数分布的概率密度函数（PDF）为： f ( x ; λ ) = { λ e − λ x if x ≥ 0 0 if x < 0 f(x; \lambda) = \begin{cases} \lambda e^{-\lambda x} & \text{if } x \geq 0

概率论(二)-随机变量及其分布：分布函数F(x)、离散型随机变量【分布律：(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度：均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度

1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布

正态分布，泊松分布，指数分布的c/c++代码

https://blog.csdn.net/u012480384/article/details/50838832

泊松分布与指数分布的理解

说到泊松分布，最好是明白：泊松分布是二项分布n很大而p很小时的一种极限形式。二项分布：已知某件事情发生的概率是p，那么做n次试验，事情发生的次数就服从二项分布。泊松分布式某段连续的时间内事情发生的次数。事情发生的时间是可以忽略的。关注的是事件的发生。泊松分布是离散的变量。这段时间是确定大小的，不是说某两件事件（不知何时发生）的间隔。把连续的时间分割层无数小份，那么每个小份之间都是相

指数分布的理解，推导与应用

指数分布的定义在浙大版的教材中，指数分布的定义如下：若连续型的随机变量 X X X的概率密度为： f ( x ) = { 1 θ e − x θ , x>0 0 , 其他 f(x) = \begin{cases} \frac{1}{\theta} e^{-\frac{x}{\theta}}, & \text{x>0}\\ 0, & \text{其他} \end{cases} f(x)={θ

AI笔记: 数学基础之连续型与均匀分布、指数分布、正态分布等

连续型随机变量及其概率密度 1 ) 连续型随机变量的概念与性质如果对于随机变量X的分布函数F(x)，存在非函数f(x), 使得对于任意实数x, 有 F ( x ) = ∫ − ∞ x f ( t ) d t F(x) = \int_{-\infty}^x f(t)dt

2024最新多目标优化算法：多目标指数分布优化器MOEDO（提供MATLAB代码）

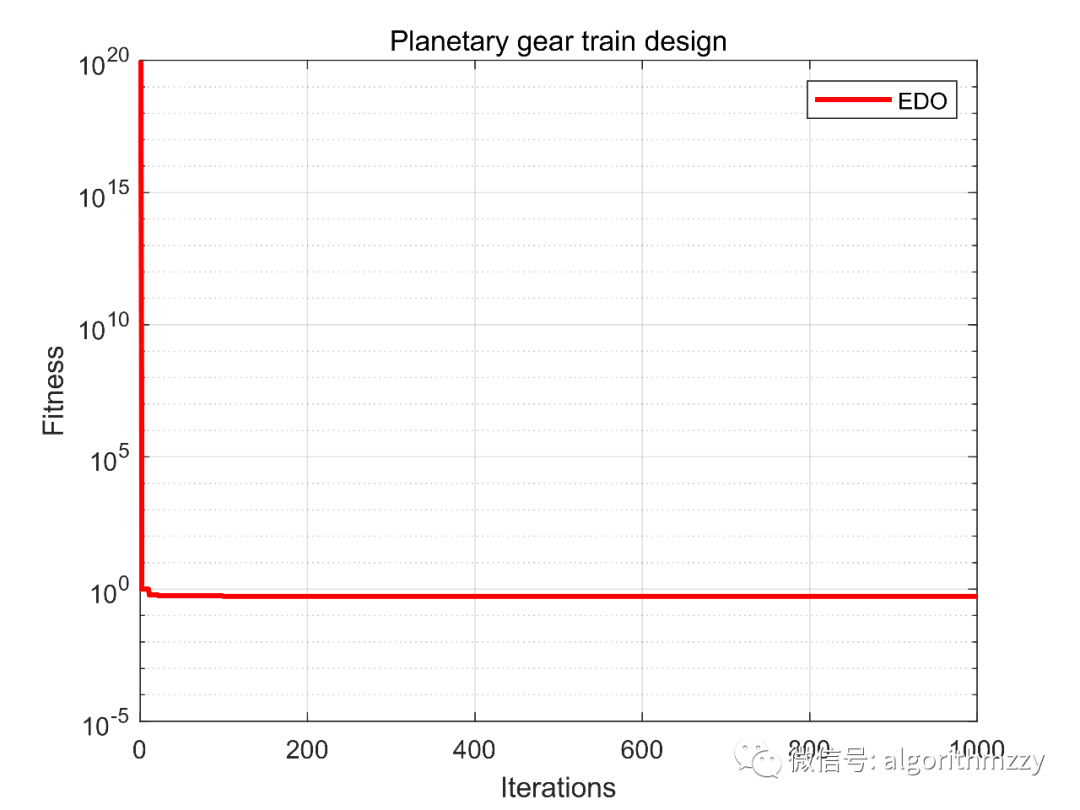
一、多目标指数分布优化器（MOEDO）多目标指数分布优化算法（Multi-objective exponential distribution optimizer ，MOEDO）由Kalita, K等人于2024年提出，其采用增强的精英非主导分类和拥挤距离机制。MOEDO集成了信息反馈机制（IFM），旨在平衡勘探和开发，从而提高收敛性并克服局部最优。 1.在指数分布优化算法EDO的基

概率基础——指数分布

概率基础——指数分布介绍指数分布是一种连续概率分布，描述了独立随机事件之间的时间间隔。它常被用来模拟随机事件的等待时间，例如到达下一位顾客的等待时间、设备故障的间隔时间等。指数分布具有无记忆性的特点，即在给定时间内没有发生事件并不会影响下一次事件发生的概率。理论及公式指数分布的概率密度函数（PDF）为： f ( x ; λ ) = λ e − λ x f(x;\lambda)

R语言贝叶斯Metropolis-Hastings Gibbs 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间

最近我们被客户要求撰写关于吉布斯采样的研究报告，包括一些图形和统计输出。指数分布是泊松过程中事件之间时间的概率分布，因此它用于预测到下一个事件的等待时间，例如，您需要在公共汽车站等待的时间，直到下一班车到了。在本文中，我们将使用指数分布，假设它的参数 λ ，即事件之间的平均时间，在某个时间点 k 发生了变化，即：我们的主要目标是使用 Gibbs 采样器在给定来自该分布的

R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...

原文链接：http://tecdat.cn/?p=26578 指数分布是泊松过程中事件之间时间的概率分布，因此它用于预测到下一个事件的等待时间，例如，您需要在公共汽车站等待的时间，直到下一班车到了（点击文末“阅读原文”获取完整代码数据）。相关视频在本文中，我们将使用指数分布，假设它的参数 λ ，即事件之间的平均时间，在某个时间点 k 发生了变化，即：我们的主要目标是使用 Gibbs

智能优化算法应用：基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用：基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码文章目录智能优化算法应用：基于指数分布算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.指数分布算法4.实验参数设定5.算法结果6.参考文献7.MATLAB代码摘要：本文主要介绍如何用指数分布算法进行3D无线传感器网(WSN)覆盖优化。

$指数分布的随机变量$