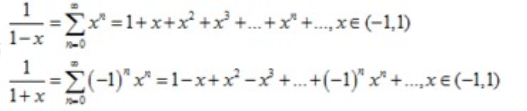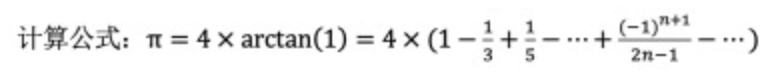习题4-2 求幂级数展开的部分和   (20分) 已知函数e^xe​x​​可以展开为幂级数1+x+x^2 /2! + x^3 /3! + \cdots + x^k /k! + \cdots1+x+x​2​​/2!+x​3​​/3!+⋯+x​k​​/k!+⋯。现给定一个实数xx，要求利用此幂级数部分和求e^xe​x​​的近似值，求和一直继续到最后一项的绝对值小于0.00001。 输入格式:

由一道题目总结幂级数的收敛域问题 @(微积分) 这个知识点可以联想阿贝尔的12块钱，即收敛区间内绝对收敛，边界需要特别讨论。 函数项级数 ∑∞n=1(2x+1)nn \sum_{n=1}^{\infty}\frac{(2x+1)^n}{n}的收敛域为 [−1,0)⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ \underline{ [-1,0)} 分析：首先想到通用形式是如何求解的。 形如 ∑∞n=0a

解题思路：求幂级数有两种方法，一种是直接法，这里显然不太好求，还有一种是利用现有展开式展开，我们看到分母 可以分解因式成(x+6)(x-1),进而拆解成一次式。拆解成一次式的目的是为了使用一下两个展开式。 第一步：分解因子(这里求出A和B的值的过程用了特殊方法，能快速计算) 第二步：拆解成一次式，利用现有展开式带入求出结果。 第三步：求x的取值范围，注意一下这里的取值范围。

实际应用中，总是会出现一堆复杂的函数，这类函数往往令物理学家和数学家都十分头疼。为了解决这一窘境，泰勒想：会不会存在一种方法，把一切函数表达式都转化为多项式函数来近似呢？这样，处理问题不就变得简单了吗？经过泰勒夜以继日的奋斗，终于研究出了泰勒级数的理论。它将一切函数，不论表达式有多么多么的复杂，只有能保证n阶导数存在，就能将它的局部用多项式展开。泰勒级数在近似计算中有重要作用。实际上，利用多项

观察 可以看到下面的结果： ∑k=1nk∑k=1nk2∑k=1nk3∑k=1nk4∑k=1nk5∑k=1nk6∑k=1nk7∑k=1nk8∑k=1nk9∑k=1nk10∑k=1nk11∑k=1nk12=n(n+1)2=n(n+1)(2n+1)6=n2(n+1)24=n(n+1)(2n+1)(3n2+3n−1)30=n2(n+1)2(2n2+2n−1)12=n(n+1)(2n+1)(3n

使用多线程，幂级数方法来计算pi，方法如下。 这样就很简单了，只要把握好线程函数的计算范围即可了。 完整程序如下 //// main.cpp// pi//// Created by Yuuki on 2020/4/29.// Copyright © 2020 Yuuki. All rights reserved.//#include <iostream>#include

要计算幂级数的近似值，可以使用以下代码： #include <stdio.h> #include <math.h> double powerSeries(double x, int n) {     double result = 1.0; // 初始化结果为级数的第一项     double term = 1.0; // 初始化当前项的值         for (int i = 1; i

已知函数e​x​​可以展开为幂级数1+x+x​2​​/2!+x​3​​/3!+⋯+x​k​​/k!+⋯。现给定一个实数x，要求利用此幂级数部分和求e​x​​的近似值，求和一直继续到最后一项的绝对值小于0.00001。‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬

转自：http://blog.sina.com.cn/s/blog_5701b67c01011u4y.html 等比数列（幂级数）的意义和应用   幂级数在理工科分析中有重要意义，其中最重要的即所谓的泰勒级数。但这里讨论其中最简单的幂级数，也就是所谓的“无穷等比数列”。                       (1) 对上式的讨论不失一般性。 对于无穷级数，自然首先要