守恒专题
用相图分析 bbr,inflight 守恒的收敛速度
以下的代码绘制了 bbr 的收敛相图: #!/opt/homebrew/bin/python3import numpy as npimport matplotlib.pyplot as pltfrom scipy.integrate import odeintdef model(vars, t, C, g):x, y = varsdxdt = C * (g * x) / (g * x + y
bbr 微观建模与 inflight 守恒
bbr 解决 bufferbloat 的核心在于一个负反馈方程,设 x 为预估带宽,x_i 为 inflt,则: d x i d t = x ⋅ R − x i \dfrac{dx_i}{dt}=x\cdot R-x_i dtdxi=x⋅R−xi 这个简单的负反馈能让数据流收住 buffer,显然,当其 inflt 大于 bdp 时,方程为负数,直到排空 buffer。如果没有这个方程
算法合集之《信息学中守恒法的应用》(不错的文章保存一下)
转载自:click here~~ 【摘要】本文提出和总结了“守恒法”,以及它在信息学竞赛中的一些应用。守恒的本质是寻找变化中的不变量。守恒法能帮助我们跳过、避开纷繁复杂的细节,直接看透问题的本质。 【关键字】守恒法 不变量 【正文】 一、 引言 现实生活和实际问题是纷繁复杂的。问题1 两个质量相等的小球,速度分别为5m/s, 4m/s,他们相向运动,完全弹性碰撞之后速度分别变成多少? 问题
inflight 守恒算法的实现和仿真
前面介绍过,只要某条流的 inflt 在 bdp 之外再增加一个相等的余量 I,即 inflt = bdp + I,比如 I = 2,I = 3,…,就一定会收敛到公平,且不会占据过多 buffer,因此 rtt 不会膨胀,I 的大小影响收敛速度,I 越大,收敛越快,但 buffer 占据也更多,I 越小,收敛越慢,但 buffer 占据更少,所以效率和公平的 tradeoff 在此体现。 记住
tcp inflight 守恒算法的自动收敛
inflight 守恒算法看起来只描述理想情况,现实很难满足,是这样吗? 从 reno 到 bbr,无论哪个算法都在描述理想情况,以 reno 和 bbr 两个极端为例,它们分别描述两种理想管道,reno 将 buffer 从恰好的 0 塞到满而保持对带宽 100% 利用,而 bbr 则通过寻求维持在 buffer 恰好为 0 的状态保持对带宽 100% 的利用,它们分别是范雅各布森管道和 bb
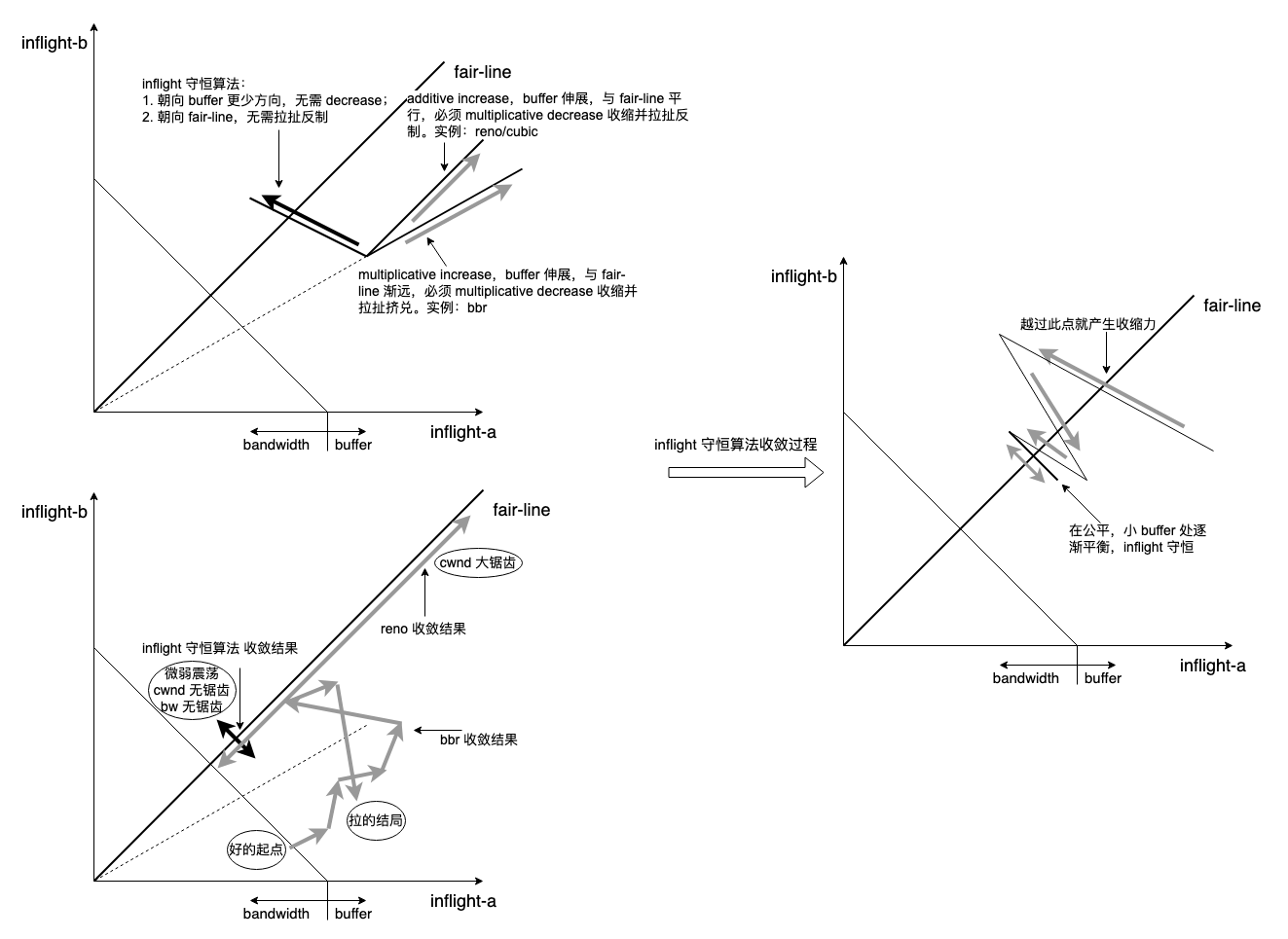
tcp inflight 守恒算法的几何解释
接上文:tcp inflight 守恒算法背后的哲学 在 tcp inflight 守恒算法正确性 中,E = bw / srtt 的公平最优解是算出来的,如果自然可以用数学描述,那能算出来的东西反过来也一定能通过直感看出来,我倾向于用几何和力学描述自然(中学时中了《几何原本》和《自然哲学的数学原理》之毒) ,inflight 守恒算法的几何解释就有了: 这就是一个初等平面几何练习题,涉及一
tcp inflight 守恒算法(tcp_ccr)
最初的算法: 在 winmax 中追踪 alpha rounds 的 bw / rtt,将其 bw 记为 b;在 winmin 中追踪 k*alpha rounds 的 rtt,记为 minrtt;保持 inflight = b * minrtt + beta。 后来我给 beta 增加了一个 rtt 缩放系数,主要是避免 rtt 膨胀,增加一个往回收缩的趋势: 保持 inflight =
物理渲染技术(PBR)守恒
PBR: PBR,或者用更通俗一些的称呼是指基于物理的渲染(Physically Based Rendering),它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。正因为基于物理的渲染目的便是为了使用一种更符合物理学规律的方式来模拟光线,因此这种渲染方式与我们原来的Phong或者Blinn-Phong光照算法相比总体上看起来要更真实一些。除了看起来更好些