复数专题

whose引导的定语从句，先行词是复数形式，从句里谓语动词用单数还是复数？

得看whose后面跟的名词，如果是复数，定语从句的谓语动词就用复数，如实单数就用单数。比如说： we live in a house whose windows are broken. we live in a house whose door is destroyed. 先行词是复数形式， whose引导的定语从句，请问，从句里谓语动词用单数还是复数？谢谢了先 - 雨露学习互助

复数的乘法

(a+bi) * (c+di) 2个向量，角度相加，长度相乘

复数的理解

a + bi 看成是把(1,0) 这个位置扯到(a, b) 这个位置。所以i就是左旋90度。所以2次i就是-1

go字符串复数

package mainimport ("fmt")func main(){ //字符串var s1 string = "hello"s2 := []rune(s1)s2[0] = 'c's3 := string(s2)fmt.Printf("%s\n",s3)//字符串换行语法s := "Starting part" +"Ending part"fmt.Printf("S'Value is:

复数-解1

个人汇总： 1、实信号对应的是实数，即二维空间的数的表示2、复信号，对应的是复数，即三维空间的数的表示复信号在信号系统中的应用是为了便于算法和处理，实际模拟复信号的运算中的I/O信号是采用实信号来模拟。复数最直观的理解就是旋转！4*i*i = -4 就是“4”在数轴上旋转了180度。那么4*i就是旋转了90度。另外，e^t是什么样呢？但当

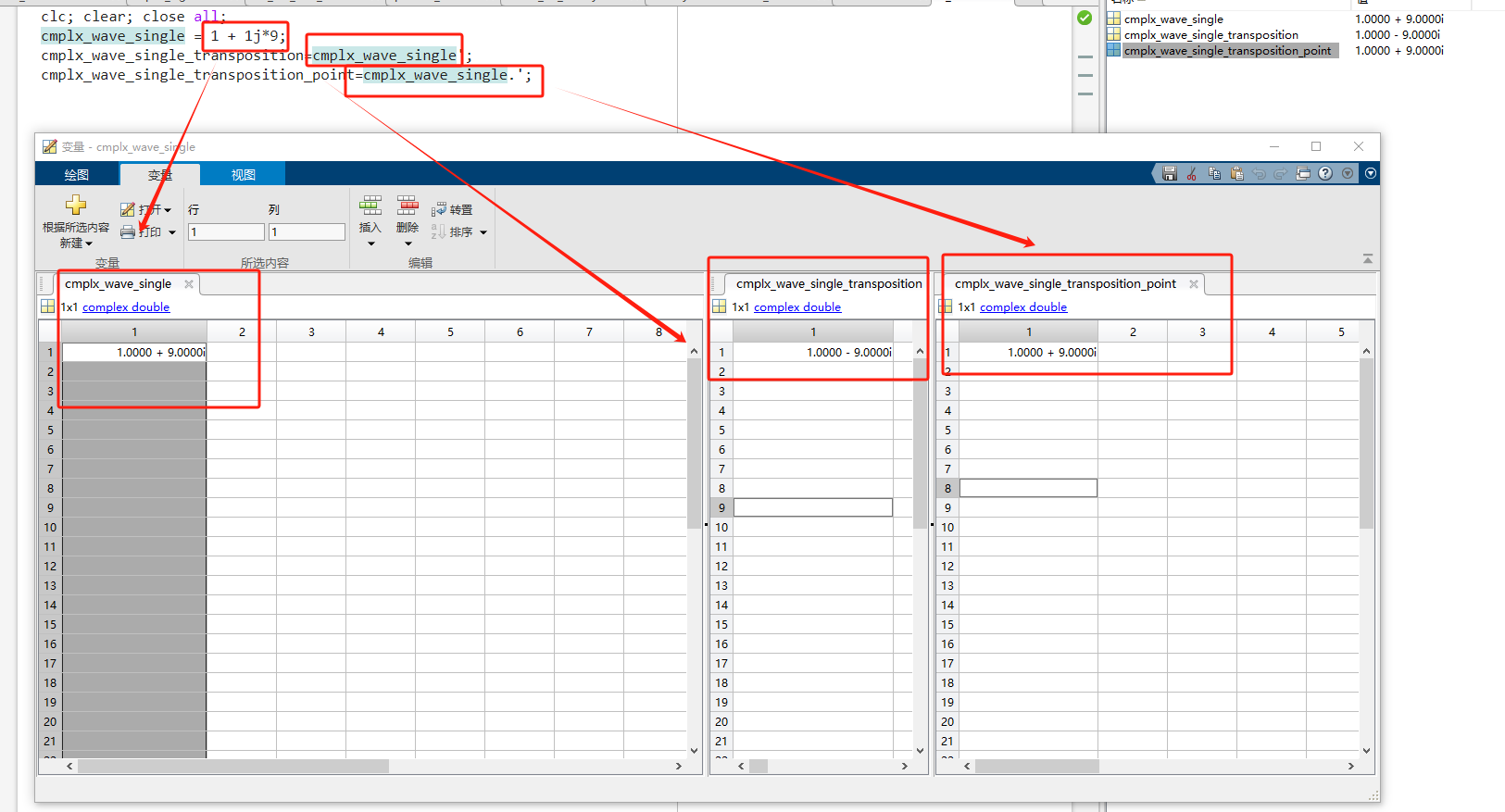
使用matlab的大坑，复数向量转置！！！！！变量区“转置变量“功能（共轭转置）、矩阵转置（默认也是共轭转置）、点转置

近期用verilog去做FFT相关的项目，需要用到matlab进行仿真然后和verilog出来的结果来做对比，然后计算误差。近期使用matlab犯了一个错误，极大的拖慢了项目进展，给我人都整emo了，因为怎么做仿真结果都不对，还好整体的代码都是我来写的，慢慢往下找就找到了问题的来源，全网没有看到多少人把这个愚蠢的错误写出来，我来引入一下。代码错误的表现：复数向量的虚部被取反，正数变成负数，负数

实数系和复数系-习题

出去有明确的相反的说明以外，本习题中所提到的数，都理解为实数 1.如果 r ( r ≠ 0 ) r\left( r\neq 0 \right) r(r=0)是有理数而 x x x是无理数，证明 r + x r + x r+x及 r x rx rx是无理数证明：假设 r + x r + x r+x是有理数，则 x = r + x − r x = r + x - r x=r+x−r是有理数，矛

复数计算 [(8+6i)*(4+3i)]/[(8+6i)+(4+3i)]= ?

计算复数 [(8+6i)*(4+3i)]/[(8+6i)+(4+3i)]= ? 复数运算规则详见百度百科 /** @Author: jinbo.ma* @Mail: 18710648068@163.com* @Date: 2021-03-11 15:02:21* @LastEditTime: 2021-03-13 16:50:20*/#include <stdio.h>typedef struc

python 复数基础

在python中复数的处理相对简单，定义一个复数通常来说有两种方式，代码如下： NB(注意): # 后面的部分表示输出结果。 class Debug:def complexDefine(self):# method 1x = 1jprint(x) # 1jprint(type(x)) # <class 'complex'># method 2x1 = complex(1, 2)print(

浮点数的复数乘法

floating point IP核I只有multiple ,没有 complex multiple 然后 complex multiple 的IP核下面只有定点的，不支持浮点，所以需要写一个浮点数的复数乘法模块。

复数乘法IP核的使用

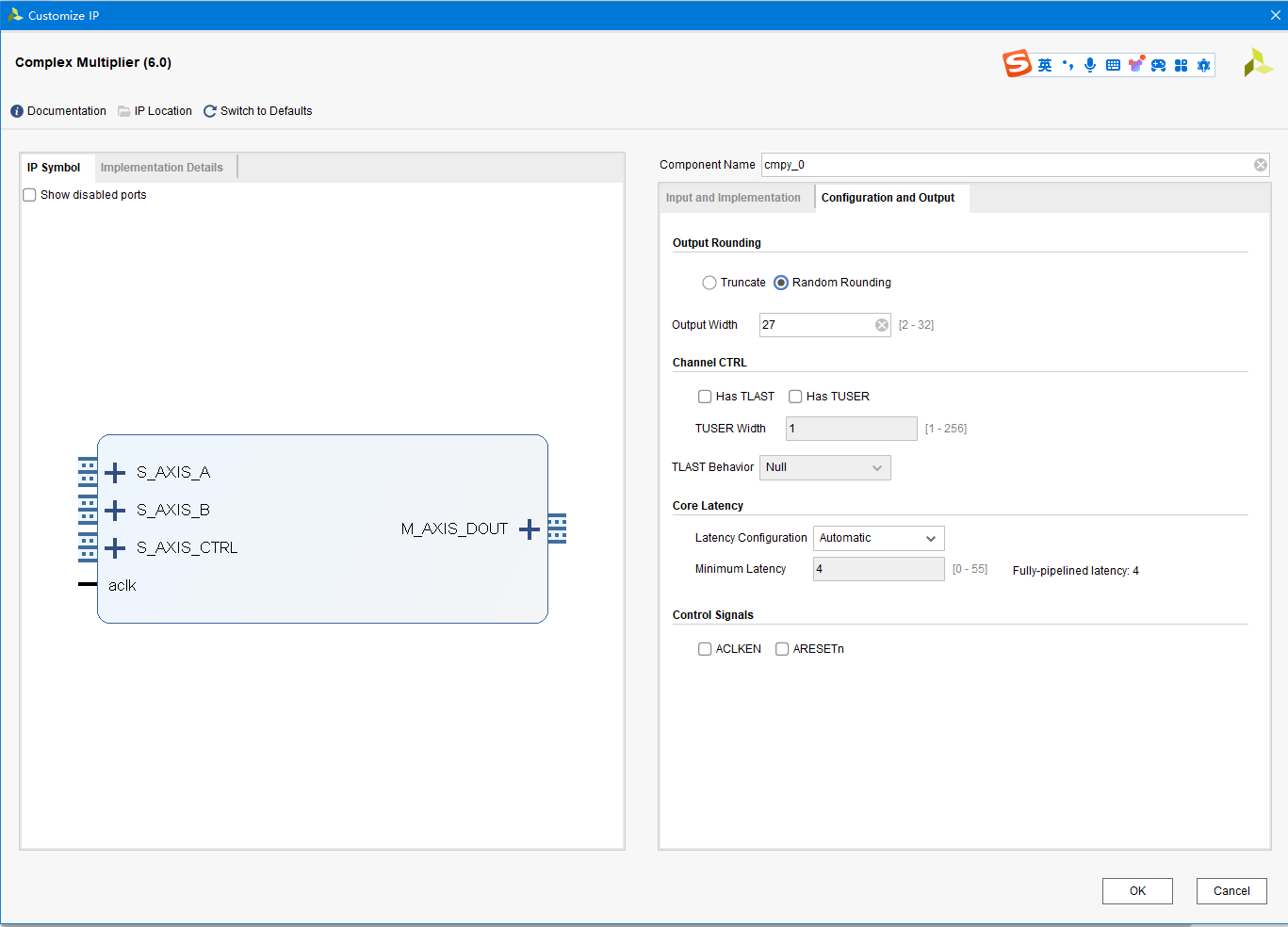
一、IP核解析在这张图片中，我们看到的是一个“Complex Multiplier (6.0)” IP 核的配置界面。以下是各个配置参数的详细说明： 1.1 Multiplier Construction Use LUTs: 选择这个选项时，乘法器将使用查找表（LUTs）来实现。这种方法通常适用于较小的操作数位宽，因为它在资源和速度之间提供了一种折衷方案。 Use Mults

C++ 实现一个复数类

要求实现⼀个复数类 Complex 。 Complex 类包括两个 double 类型的成员 real 和 image ，分别表示复数的实部和虚部。对 Complex 类，重载其流提取、流插⼊运算符，以及加减乘除四则运算运算符。重载流提取运算符 >> ，使之可以读⼊以下格式的输⼊(两个数值之间使⽤空⽩分隔)，将第⼀个数值存为复数的实部，将第⼆个数值存为复数的虚部： -1.1 2.0

怎么理解虚数和复数

在实数域中，连接两个真理的最短的路径是通过复数域----雅克·阿达马现代数学家对复数的看法如斯，无限拔高了复数的地位，这样说有道理吗？ 1 对于复数的普通认知我想，对于复数，或许大家一般会有以下的认知吧。 1.1 应付考试高中的时候，会粗略地学习下复数，首先定义：然后形如：这样的数就是复数。有了复数之后，开方运算就不再局限于大于0的数了，这样高中必考的一元

复数在坐标系中表示

1.复数概念：形式如z=a+bi（a,b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当z的虚部等于零时，常称z为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。2.例如：z = 3+2i是复数，它的实部为3(x轴横坐标)，虚部为2(y轴纵坐标).z = 1 + 2i 对应坐标：(1,2); 2i表示以1+2的平开再开方的长度,左旋90度.z² = (1 +

在复数类中自定义类型转换函数实现复数和非复数之间的运算

实现复数+double型数据，并且打印运算后实部上的数据 #include <iostream>using namespace std;class Complex {public:Complex( )//定义默认构造函数初始化复数{real=0;imag=0;} //使用初始化表初始化复数Complex(double r, double i):real(r),imag(i)

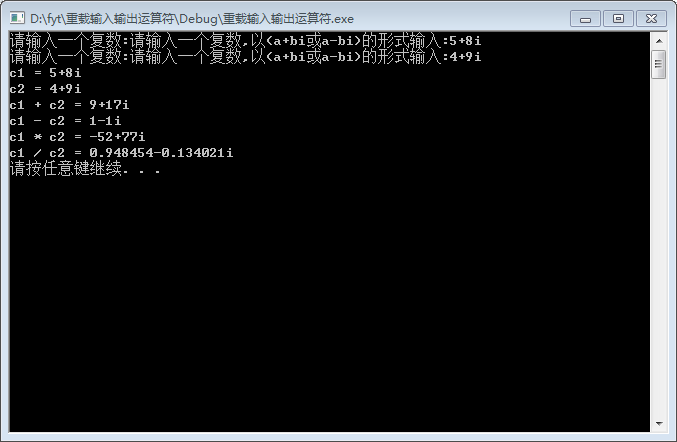
通过重载输入和输出运算符实现复数的输入和输出

程序代码: #include <iostream>using namespace std;class Complex {public:Complex( )//定义默认构造函数初始化复数{real=0;imag=0;} //使用初始化表初始化复数Complex(double r, double i):real(r),imag(i){}Complex operator+(Com

傅里叶变化的本质：复数的实部和虚部的对应关系

之前做计算光学成像，需要用到图像的相位信息。但是设计到傅里叶变化的实部和虚部的问题的时候，发现教科书上一般来讲，只会介绍一句：如果f(x,y)是实函数，则它的傅里叶变化就是关于原点共轭对称的： F(u,v) = F*(-u,-v) 也就是说傅里叶谱关于原点对称。但是，当原函数f(x,y)不是实数的时候呢然后我经过测

【C++例题】复数类加减法运算重载—成员函数形式

知识点： 1.两个不同位置的const的不同意义 2.形参有默认值的函数只能在类内给出，类外不能多余声明，即使默认值一样 3.创建一个临时对象调用的是构造函数而非默认的复制构造函数 4.重载的运算符可以当成普通运算符使用，但是要注意其本质是函数调用，要注意本体对象和传入参数的位置 //例8-1_复数类加减法运算重载—成员函数形式#include<iostream>using name

OpenCV-复数矩阵点乘ComplexMatrixDotMultiplication

实数系和复数系

实数系和复数系导引 1.1 例我们现在证明方程 p 2 = 2 p^2 = 2 p2=2 不能被任何有理数 p p p满足，倘若有那样一个 p p p，我们可以把它写成 p = m n p = \frac{m}{n} p=nm,其中 m m m和 n n n都是整数，而且可以选得不都是偶数，代入得 m 2 = 2 n 2 m^2 = 2 n^2 m2=2n2 表明 m 2 m^2 m

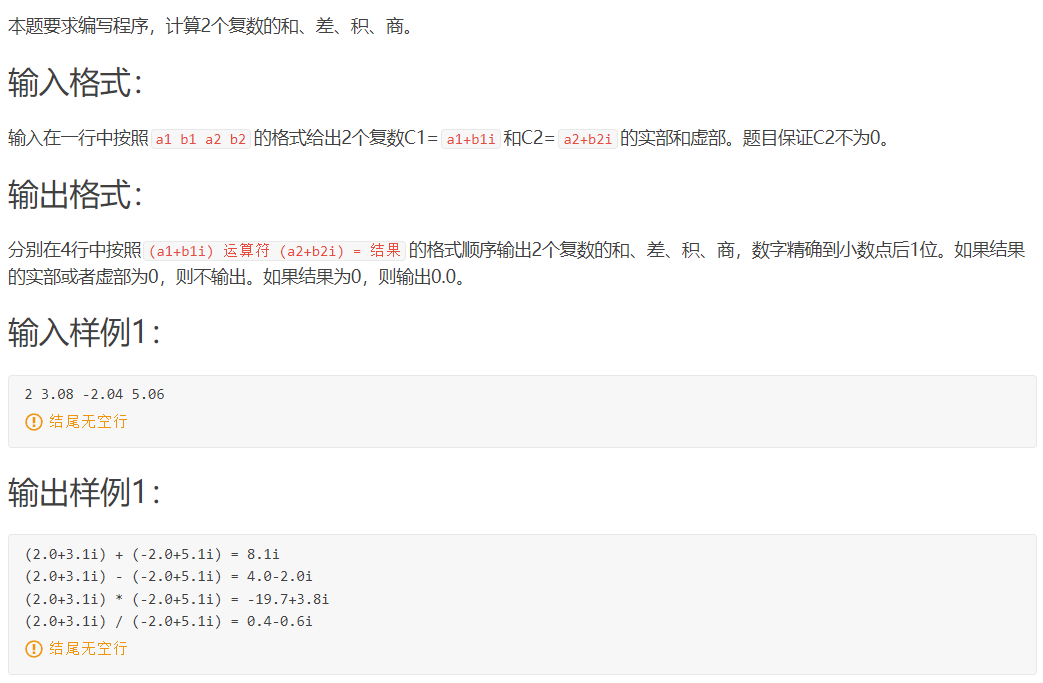
7-36 | 复数四则运算

题目：解答：个人认为需要注意的地方是对负数的四舍五入； #include "stdio.h"#include "math.h"void rounding(float *f){int flag=*f<0?-1:1; int i=abs((int)(*f*100));if(i%10<5){i=i/10; }else{i=i/10+1;}*f=flag==1?(float)i/10

第6周项目6--复数模板类-友元

复数与二维空间旋转

引言 ⚠️ 本文充斥了大量的数学，但是不用担心，已发给高中生表弟，他表示能看懂。看完就能理解为什么在复平面中乘 i i i相当于逆时针旋转90°。复数概念简介复数被称为是数字之王，可能是因为它们可以解决普通实数不能解决的问题。比如对于以下看起来无解的方程： 1 + x 2 = 0 1 + x^2 = 0 1+x2=0 确实没有实数解，这会得到： x = − 1 x = \sq

3.4 Python复数类型（complex）

Python复数类型（complex）详解复数（Complex）是 Python的内置类型，直接书写即可。换句话说，Python 语言本身就支持复数，而不依赖于标准库或者第三方库。复数由实部（real）和虚部（imag）构成，在 Python 中，复数的虚部以j或者J作为后缀，具体格式为： a + bj a 表示实部，b 表示虚部。【实例】Python 复数的使用： c1 = 1

线性代数笔记25--复数矩阵、快速傅里叶变换

1. 复数矩阵复向量 Z = [ z 1 z 2 z 3 z 4 ⋯ ] Z=\begin{bmatrix} z_1\\z_2\\z_3\\z_4\\ \cdots \end{bmatrix} Z= z1z2z3z4⋯ 复向量的模长 ∣ z ∣ = z ‾ ⊤ z = [ z ‾ 1 z ‾ 2 z ‾ 3 ] [ z 1 z 2 z 3 ] \lvert z\r

二次方程式 ax**2 + bx + c = 0（用python实现，区分实数根与复数根）

import mathimport cmathdef sol(a,b,c):#判断b的平方是否大于4ac,大于等于的时候是实数根，小于的时候是复数根（cmath相比与math的区别是cmath是复数运算）if b**2 >= 4*a*c :sqrt = math.sqrt(b**2 - 4*a*c)x1 = (-b + sqrt) / (2 * a)x2 = (-b - sqrt) / (2 *