本文主要是介绍傅里叶变化的本质:复数的实部和虚部的对应关系,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
之前做计算光学成像,需要用到图像的相位信息。但是设计到傅里叶变化的实部和虚部的问题的时候,发现教科书上一般来讲,只会介绍一句:
如果f(x,y)是实函数,则它的傅里叶变化就是关于原点共轭对称的:
F(u,v) = F*(-u,-v)
也就是说 傅里叶谱关于原点对称。
但是,当原函数f(x,y)不是实数的时候呢
然后我经过测试:
输入:
原信号实部
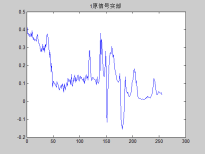
原信号虚部
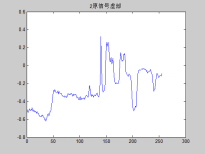
上面两个一维信号 构成 一个 复数的 输入信号。
然后把上面复数信号经过fft得到
实部 和 虚部
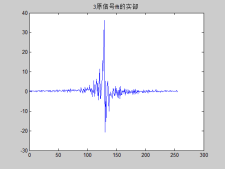

再来, 原信号的 实部fft得到的 实部和虚部:
可以看到 是:偶对称的实部 和 奇对称的虚部

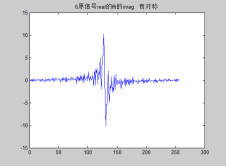
再来, 原信号的 虚部 fft 得到的 实部和虚部:
可以看到 是:奇对称的实部 和 偶对称的虚部

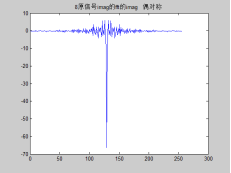
最后,原信号的实部的fft得到的实部 + 原信号的虚部的fft得到的实部
可以看到和 原信号直接fft的实部 是一样的

最后,原信号的实部的fft得到的虚部 + 原信号的虚部的fft得到的虚部
可以看到和 原信号直接fft的虚部 是一样的

说明:
傅里叶变换中的对称性:
时域信号的实部对应频谱为偶对称实部和奇对称虚部
时域信号的虚部对应频谱为奇对称实部和偶对称虚部
时域信号包含实部和虚部时,频谱是两者的叠加

够不够清晰?
明白了吧?
你要是还不明白,那...就给我留言吧~
这篇关于傅里叶变化的本质:复数的实部和虚部的对应关系的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






