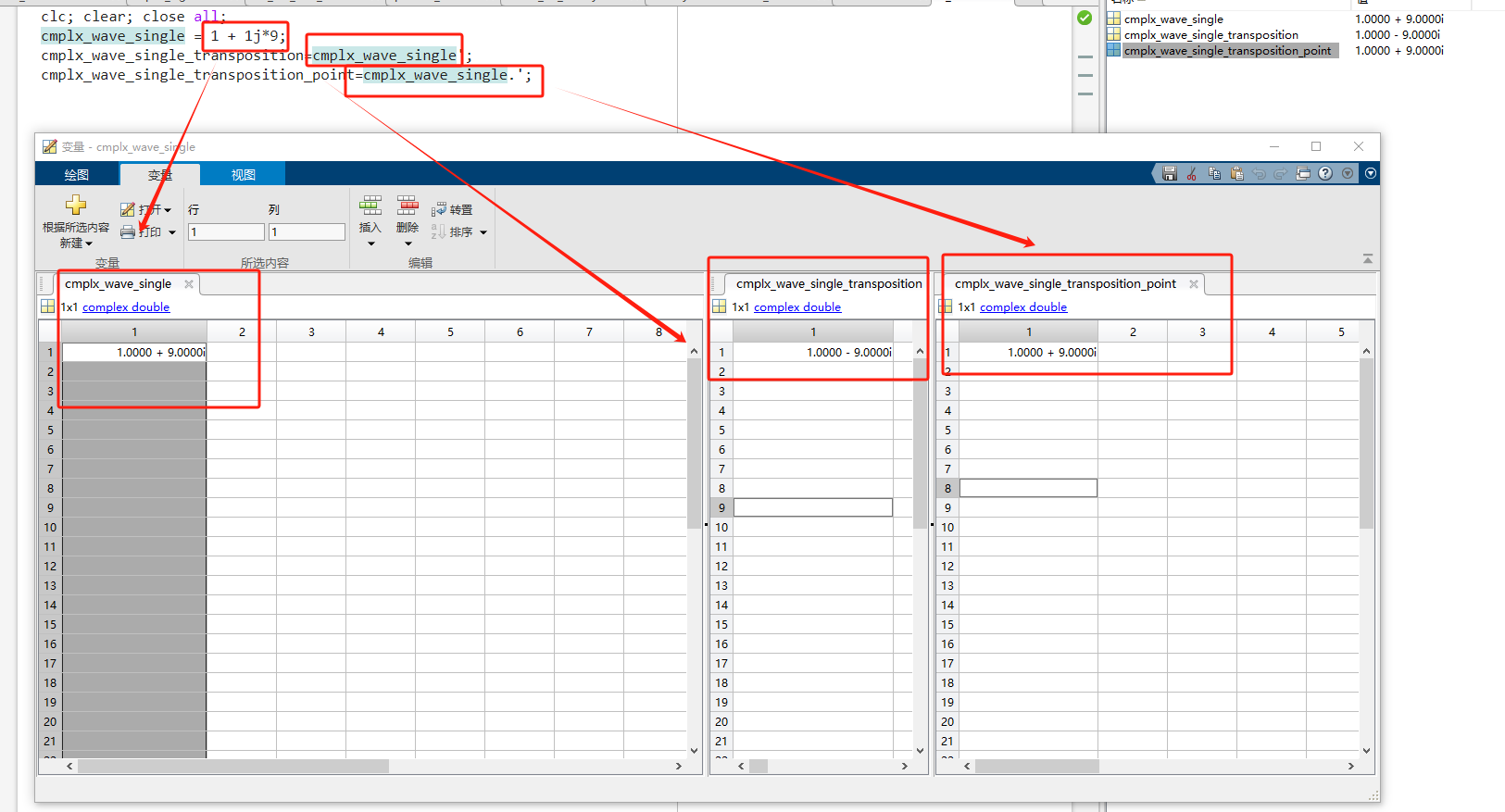
本文主要是介绍复数-解1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
个人汇总:
1、实信号对应的是实数,即二维空间的数的表示
2、复信号,对应的是复数,即三维空间的数的表示复信号在信号系统中的应用是为了便于算法和处理,实际模拟复信号的运算中的I/O信号是采用实信号来模拟。
复数最直观的理解就是旋转!
4*i*i = -4就是“4”在数轴上旋转了180度。
那么4*i就是旋转了90度。
另外,e^t是什么样呢?
但当你在指数上加上i之后呢?
变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
当然,更重要的意义在于复数运算保留了二维信息。
假如我让你计算3+5,虽然你可以轻松的计算出8,但是如果让你分解8你会有无数种分解的方法,3和5原始在各自维度上的信息被覆盖了。
但是计算3+5i的话,你依然可以分解出实部和虚部,就像上图那样。
基于以上两个理由,用复数来描述电场与磁场简直完美到爆棚!
我们即可以让电场强度与复数磁场强度相加而不损失各自的信息,又满足了电场与磁场90度垂直的要求。另外,一旦我们需要让任何一个场旋转90度,只要乘一个“i”就可以了
受 @physixfan 答案的提醒,再补充一点。
正弦波在频域可以看作是自然数中的“1”,可以构成其他数字的基础元素。当你需要5的时候,你可以看成是1*5(基础元素的五倍)也看以看成2+3(一个基础元素2倍与基础元素3倍的和)。这些用基础元素构成新元素的运算是线性运算。
但是现在你如何用线性运算吧2sin(wt)变换成4sin(wt+pi/6)呢?
利用欧拉公式,我们可以将任何一个正弦波看作其在实轴上的投影。假如两个不同的正弦波,可以用数学表达为:
这种用复指数来计算正弦波的方法也对电磁波极其适用,因为电磁波都是正弦波,当我们需要一个电磁波在时间上延迟/提前,或是在空间上前移/后移,只需要乘一个复指数就可以完成对相位的调整了。
这篇关于复数-解1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!