复变专题
复变函数在大模型中的应用
1. 导入 说来惭愧，我研究生时的研究方向是复分析，但毕业近十年来几乎没用到它。 我还记得实习时做自我介绍时，我说我的研究方向是复分析。面试官不太了解，我便解释说，这是关于对 -1 开平方得到的虚数 i 的研究。 在人工智能领域，经常会用到的数学知识包括矩阵、概率论和一些微积分。然而，最近在研究大模型的位置编码时，我惊讶地发现了复分析的应用，10年前的记忆逐渐浮现。 2. 什么是复数 复
你好，复变函数2.0
第一行：0 或 1 第二行：（空格）+函数（后缀） #pragma warning(disable:4996)#include <easyx.h>#include <stdio.h>#include <math.h>#define PI 3.141592653589793#define E 2.718281828459045#define K (1.0 / 256.0
复变函数及应用 第四章学习感受
复变函数的积分其实相当于曲线积分，参数的变化引起(x,y)的变化，进而代表积分变量z的变化。但是如果每个积分都这么做就太麻烦了。能不能向1元函数那样直接对自变量z做积分呢？书中告诉我们，对于连续函数，以下3个结论等价： 1.f(z)存在原函数F(z) 2.f(z)的积分只与积分的起点和终点有关，与积分路径无关 3.f(z)延闭围道的积分为0 如果说上面的结论还有点“微积分”的感觉吧
复变函数及应用 第三章学习感受
中秋3天去北京玩，路上高铁来回大约也有10个小时了，忙里偷闲的看完了第3章。这一章讲的是初等函数，但是自变量从实数扩展到了复数。问题主要出现在了指数函数具有周期性，所以对数函数就要考虑主值问题，所以实变量中的很多对数等式就不一定成立了。其他的还好，尤其是双曲正余弦与普通的正余弦关系更加紧密了。其他就没啥了，就是习题略多，不过大部分稍微难度的题目都给出了提示的。
复变函数及应用 第一章学习感受
第一章讲的是复数，基本上都是些中学的内容，所以先说点其他的。 首先是教材，《复变函数及应用》这本书英文版都已经有第9版了，但是中文版只翻译到第7版，而且中文版已经绝版了，要买只能在淘宝上买复印版的，或者二手书。（我的买的就是二手书，可是此书以前的主人对它不甚爱惜，也可能是太旧了，所以书看起来不是那么赏心悦目，而且圈点勾画的也比较凌乱）。其次吐槽一下这本书的翻译，虽然我因为自己啃过英文原版，所以
复变函数论(一)-复数与复变函数01-复数02：复平面【复数z=x+iy由一对有序实数(x,y)唯一确定；(x,y) 就称为复数z的实数对形式】【表示复数z的平面称为复平面；x轴：实轴；y轴：虚轴】
一个复数 z = x + i y z=x+\mathrm{i} y z=x+iy 本质上由一对有序实数 ( x , y ) (x, y) (x,y) 惟一确定, ( x , y ) (x, y) (x,y) 就称为复数 z z z 的实数对形式. 于是能够建立平面上全部的点和全体复数间的一一对应关系. 换句话说, 我们可以借助于横坐标为 x x x 、纵坐标为 y y y 的点
![[渝粤教育] 四川师范大学 复变函数与积分变换 参考 资料](http://edu-image.nosdn.127.net/CDE205944DA88C23B1139314398B9B60.png?imageView&thumbnail=520x520&quality=100)
[渝粤教育] 四川师范大学 复变函数与积分变换 参考 资料
教育 -复变函数与积分变换-章节资料考试资料-四川师范大学【】 第一章单元作业题 第一章单元测验题 1、【单选题】 A、 B、 C、 D、 参考资料【 】 2、【单选题】 A、 B、 C、 D、 参考资料【 】 3、【单选题】 A、 B、 C、 D、 参考资料【 】 4、【单选题】 A、 B、 C、 D、 参考资料【 】 5、【单选题】 A、 B、 C、 D、 参考资料【 】 6、【单选题
【复变函数笔记】傅里叶变换和拉普拉斯变换
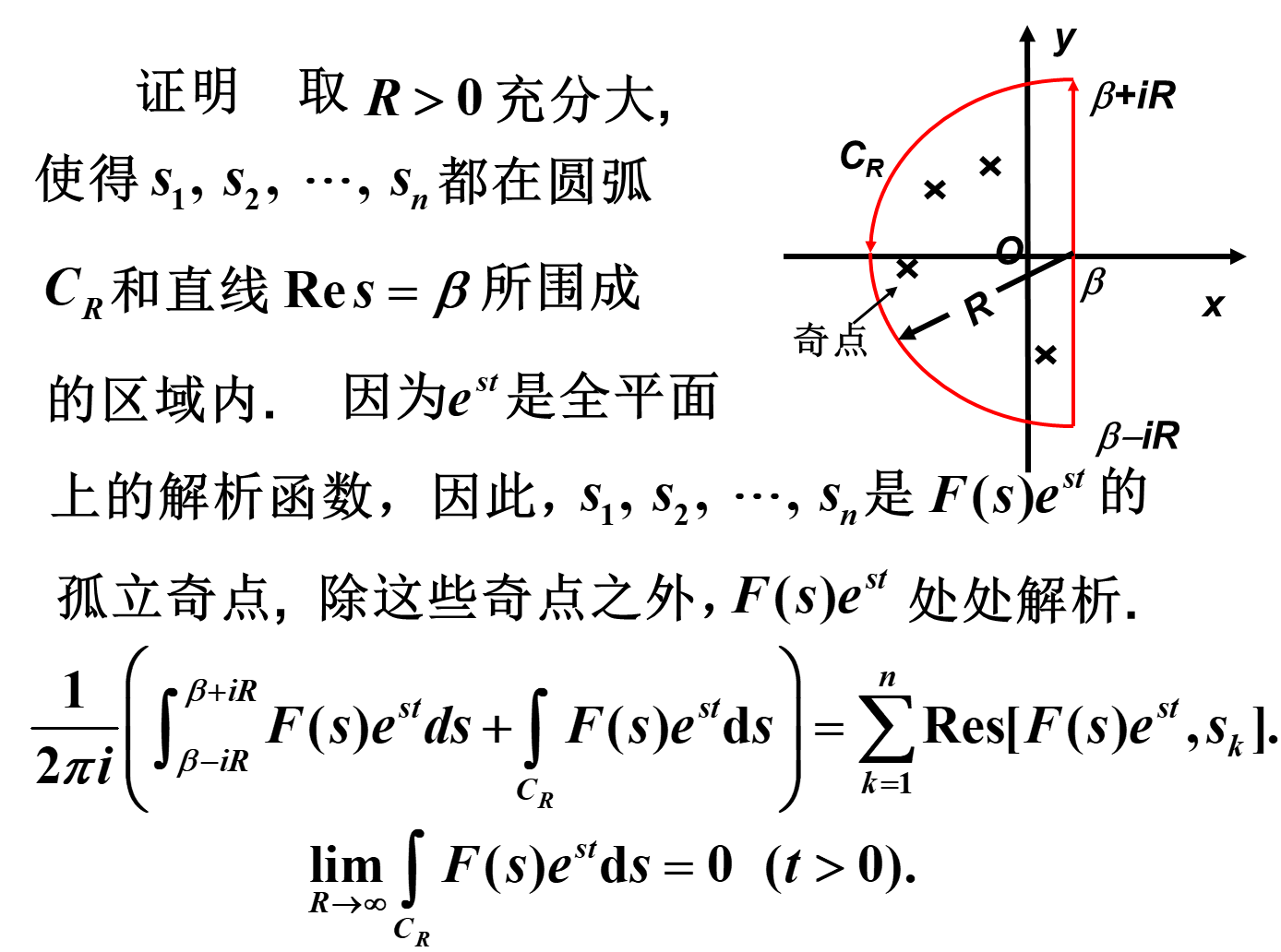
文章目录 一、傅里叶变换和拉普拉斯变换的定义1. 傅里叶积分2. 傅里叶变换3. 单位脉冲函数和单位阶跃函数4. 拉普拉斯变换 二、常见函数的傅里叶变换和拉普拉斯变换三、傅里叶变换和拉普拉斯变换的性质四、拉普拉斯逆变换 一、傅里叶变换和拉普拉斯变换的定义 1. 傅里叶积分 傅里叶积分定理 若 f ( t ) f(t) f(t)在 ( − ∞ , + ∞ ) (-\infty,+
通信入门系列——复变函数
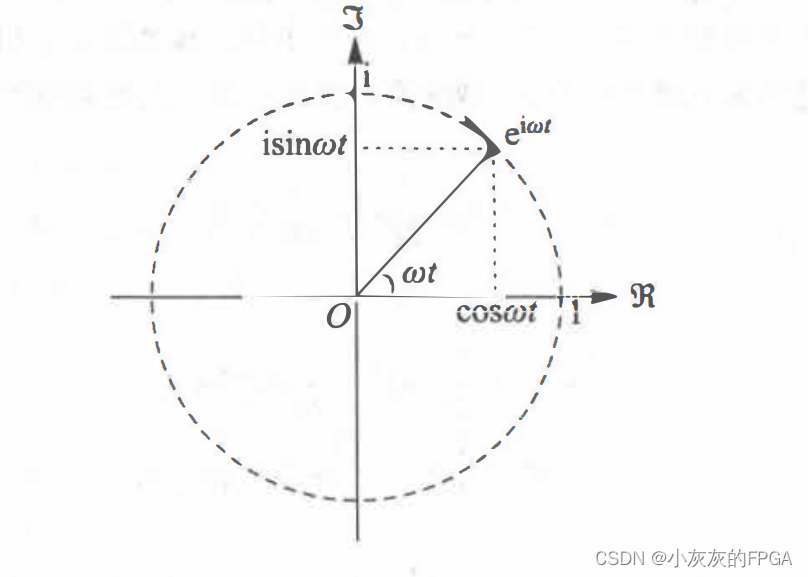
本节目录 一、复变函数1、复数2、复数的四则运算二、复指数函数三、欧拉公式 本节内容 一、复变函数 1、复数 复数单位i，也就是满足i^2=-1，将z=x+iy表示为复数z，x和y为任意的实数，称为复数z的实部和虚部。由复数z=x+iy对应的点(x,y)组成的二维平面，称为复平面，也叫作高斯平面。复平面上的点，可以用模和幅度角来进行表示,横坐标为实部，纵坐标为虚部，r表示复数的模，θ