计科顶流必背复变

本文主要是介绍计科顶流必背复变，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

复变函数B-重难点

第一章、复数和平面点集

$z = x + iy, x = Rez, y = Imz$
四则运算同实数，满足交换律、结合律、分配律
$z\overline{z} = (Rez)^2+(Imz)^2=\vert z\vert^2$
$\begin{cases}\vert{Rez}\vert \\ \vert Imz \vert \end{cases} \leq \vert z\vert \leq \vert Rez \vert + \vert Imz\vert$
满足三角不等式及其推论
$Argz = argz + 2k\pi$
由 $z=e^{i\phi}$ 得
- $z_1z_2=r_1r_2e^{i(\phi_1+\phi_2)}$
- $\frac{z_1}{z_2}=\frac{r_1}{r_2}e^{i(\phi_1-\phi_2)}$
- $z^n=r^ne^{in\phi}=r^n(\cos{n\phi} +i\sin{n\phi})$
- $\sqrt[n]{z}=(\sqrt[n]{r}(\cos{\frac{\phi+2k\pi}{n}}+i\sin{\frac{\phi+2k\pi}{n}}))(k=0,1,\dots,n-1)$
复数极限同实数极限，且实部和虚部同时取对应极限
非空点集D是区域满足两个条件
- D是开集
- D中任意两点可以用一条全在D的折线连接起来（即D具有连通性）

第二章、复变数函数

一一对应为单值函数，一多对应为多值函数
w=f(z)是集合E上的单值函数，其中中，若任意两个不同z的对应w不同，称w=f(z)是集合E中的一个一一映照
函数极限与连续性同实数
设w=f(z)在点z的某个邻域U内有定义， $z+\Delta z\in U$ .如果极限 $\lim\limits_{\Delta z\rightarrow 0} \frac{f(z+\Delta z)-f(z)}{\Delta z}$ 存在，就称函数f(z)在点z可微，且这个极限成为f(z)在点z的导数或微商。
如果f(z)在区域D内的，每一点可微，则称f(z)在D内解析，或者说f(z)是D内的解析函数；如果f(z)在点z_0的某个邻域内可微，则称f(z)在点z_0解析；如果f(z)在点z_0不解析，则z_0称为f(z)的奇点
C-R方程，可微的充要条件 $\begin{cases}\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \\ \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}\end{cases}$

初等函数
- 指数函数
  - $e^z=e^xe^{iy}=e^x(\cos y+i\sin y)$
  - $e^z$ 是一个以 $2\pi i$ 为周期的周期函数。
  - $e^{z_1}=e^{z_2}$ 的充要条件是 $z_1-z_2=2k\pi i(k \in Z)$
  - 全平面解析
- 三角函数和双曲函数
  - $\sin z=\frac{1}{2i}(e^{iz}-e^{-iz})$
  - $\cos z=\frac{1}{2}(e^{iz}+e^{-iz})$
  - $\sinh z=\frac{1}{2}(e^z-e^{-z})$
  - $\cosh z=\frac{1}{2}(e^z+e^{-z})$
  - 实三角函数的恒等式对复变数仍成立
  - 全平面解析
- 对数函数
  - 满足方程e^w=z的负数w成为z的对数,记作 $w = Lnz$
  - $Lnz=ln\vert z\vert+iArgz=ln\vert z\vert+i(argz+2k\pi)$
  - 多值函数，任选一单支可表示为 $lnz=ln\vert z\vert+iargz(-\pi\lneq argz\leq \pi)$
  - 每个单支都是一个解析函数，上述单支是沿负实轴割开了的z平面区域D内的解析函数
- 一般幂函数
  - $\alpha$ 是任意给定的复数，对于复变数 $z\neq 0$ ，定义z的 $\alpha$ 次幂函数为 $w=z^\alpha=\exp\{\alpha Lnz\}=\exp\{\alpha[ln\vert z\vert+i(argz+2k\pi)]\}$
  - 可能是单值、有限多值或无限多值函数
    - $\alpha$ 为正整数n时， $\exp\{i2k\pi n\}=1$ ，所以 $z^n=\exp\{n(ln\vert z\vert+iargz)\}=\vert z\vert^n\exp\{inargz\}$ ,它是单值函数
    - 当 $\small \alpha=\frac{1}{n}$ 时， $z^{\frac{1}{n}}=\vert z\vert^{\frac{1}{n}}\exp\{i\frac{argz+2k\pi}{n}\}$ ，n个单值分支
    - 当 $\alpha$ 为无理数或一般复数时， $z^\alpha$ 是无穷多值的。
  - 单值、无穷多值全平面解析，有限多值为沿主值边界割开了的z平面区域解析
- 反三角函数(注：所有根式为双值函数)
  - $z=\sin w$ 有 $w=Arcsinz$ ,解方程得， $Arcsinz=-iLn(iz+\sqrt[]{1-z^2})$
  - 同理有
    - $Arccosz=-iLn(z+\sqrt[]{z^2-1})$
    - $Arctgz=-\frac{i}{2}Ln\frac{1+iz}{1-iz}$
    - $Arcshz=Ln(z+\sqrt[]{z^2+1})$
    - $Arcchz=Ln(z+\sqrt[]{z^2-1})$
    - $Arcthz=\frac{1}{2}Ln\frac{1+z}{1-z}$
  - 均为多值函数

第三章、解析函数的积分表示

设f(z)=u(x,y)+iv(x,y)在曲线C上连续，则复积分 $\int_cf(z)dz$ 存在，而且 $\int_cf(z)dz=\int_cu(x,y)dx-v(x,y)dy+i\int_cv(x,y)dx+u(x,y)dy$ 。（证明： $\int_c(u+iv)(dx+idy)$ )
可采用换元法 $\int_cf(z)dz=\int_a^bf(z(t))z'(t)dt$
一个重要积分：设n是整数，C是以a点为中心，R为半径的圆周，试按逆时针方向计算积分 $I=\int_c\frac{dz}{(z-a)^n}$
- 取 $z=Re^{i\theta}$ ，故 $I=\frac{i}{R^{n-1}}\int_0^{2\pi}e^{i(1-n)\theta}d\theta = \begin{cases}2\pi i& (n=1)\\ 0&(n\neq1)\end{cases}$
(长大不等式)若曲线C上有 $\vert f(z)\vert \leq M$ ，曲线C的长为l,则有
$\vert\int_cf(z)dz\vert \leq Ml$
(Cauchy积分定理)设D是由闭路C所围成的单连通区域，f(z)在闭域 $\overline D=C+D$ 上解析，则 $\int_cf(z)dz=0$
- 设f(z)在单连通域D内解析，C是D内的任意封闭曲线，则 $\int_cf(z)dz=0$
- 设f(z)在单连通域D内解析，C是D内一条起于点 $z_0$ 而终于点 $z$ 的简单曲线，则积分 $\int_cf(\zeta)d\zeta$ 的值不依赖于积分路径C，而只由 $z_0$ 及 $z$ 确定，所以可记为 $\int_{z_0}^zf(\zeta)d\zeta$
(多连通区域的Cauchy积分定理)设f(z)在复闭路 $C=C_0+C_1^-+C_2^-+\cdots+C_n^-$ 及其所围成的多连通区域内解析，则 $\int_{c_0}f(z)dz=\int_{c_1}f(z)dz+\int_{c_2}f(z)dz+\cdots+\int_{c_n}f(z)dz$ 或 $\int_cf(z)dz=0$
Cauchy积分公式
- 设函数f(z)在闭路C及其所围成的区域D内解析，则对D内任一点z，有 $f(z)=\frac{1}{2\pi i}\int_c\frac{f(\zeta)}{\zeta-z}d\zeta$
- 设函数f(z)在闭路C及其所围成的区域D内解析，则对D内任一点z，f(z)有任意阶导数，且 $f^{(n)}(z) = \frac{n!}{2\pi i}\int_c\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta$
设f(z)在单连通区域D内连续，且对D内任意闭路C，有 $\int_cf(z)dz=0$ ,那么，由变上限的积分所确定的函数 $F(z)=\int_{z_0}^zf(z)dz$ 是D内的解析函数，而且 $F'(z)=f(z)(z\in D)$
- 设f(z)在单连通区域D内解析，上述结论也成立
- 在上述推论条件下，对 $f(z)$ 任一原函数 $H(z)$ ，有牛顿-莱布尼兹公式， $F(z)=\int_{z_0}^zf(z)dz = H(z)-H(z_0)$
(Morera定理) 设f(z)在单连通区域D内连续，且对D内任意闭路C，有 $\int_cf(z)dz=0$ ，则f(z)在D内解析
实二元函数u(x,y)在区域D内有二阶连续偏导数，且在D内满足Lapace方程， $\frac{\partial^2u}{\partial x^2}+\frac{\partial^2v}{\partial y^2}=0$ ，称 $u(x,y)$ 是域D内的调和函数。
设f(z)=u(x,y)+iv(x,y)在域D内解析，那么它的实部u和虚部v都是D内的调和函数

第四章、解析函数的级数表示

设有复数列 $\{z_n=x_n+iy_n,n=1,2,\dots\}$ ，表达式 $\sum_{k=1}^nz_k=z_1+z_2+\dots+z_k+\cdots$ ，称为复数项无穷级数。如果它的部分和数列 $S_n=z_1+z_2+\dots+z_n(n=1,2,\dots)$ 有极限 $\lim\limits_{n\rightarrow+\infty}S_n=S=a+ib$ ，则称级数收敛，S为级数的和。
复级数收敛的充要条件是实部与虚部级数均收敛
复级数的收敛必要条件是 $\lim\limits_{n\rightarrow+\infty}z_n=0$
$\sum_{n=0}^{+\infty}a_n(z-a)^n=a_0+a_1(z-a)+a_2(z-a)^2+\cdots$ 称为幂级数。如果 $\sum_{n=0}^{+\infty}a_n(z-a)^n$ 收敛，则称幂级数在点 $z_0$ 收敛。
(Abel定理)如果幂级数在某点 $z_0$ 收敛，则它在圆 $\vert z-a\vert < \vert z_0-a\vert$ 内绝对收敛。如果幂级数在某点 $z_1$ 发散，则它在圆外域 $\vert z-a\vert > \vert z_1-a\vert$ 内处处发散。
研究复幂级数的收敛域，考虑与它相应的实幂级数 $\sum_{n=0}^{+\infty}\vert a_n\vert x^n$ (x为实变数)：
- 若 $0<R<+\infty$ ，则复幂级数在圆 $D:\vert z-a\vert < R$ 内绝对收敛；在圆外域 $\vert z-a\vert > R$ 内处处发散。
- 若 $R=+\infty$ ，则复幂级数在全平面内收敛
- 若 $R=0$ ，则复幂级数只在复平面内一点 $z=a$ 收敛
R由实幂级数公式进行计算
复幂级数在收敛圆内可以逐项求导和逐项积分
在收敛圆内，幂级数的和函数f(z)解析，且系数 $a_k=\frac{f^{(k)}(a)}{k!}(k=0,1,2,\cdots)$ 。

设函数f(z)在点a解析，以a为中心做一个圆，并让圆的半径不断扩大，直到圆周碰上f(z)的奇点为止，则在此圆域内可展开成幂级数 $f(z)=\sum_{n=0}^{+\infty}a_n(z-a)^n$ , 其中 $a_n=\frac{f^{(n)}(a)}{n!}$ 。
- 函数f(z)在它的任一解析点的泰勒展开是唯一的
- 幂级数即是它的和函数在收敛圆内的泰勒展开
f(z)在区域D内解析的充要条件是f(z)在D内任一点a处可以展开成 $z-a$ 的幂级数。
$f(z) = a_m(z-z_0)^m+a_{m+1}(z-z_0)^{m+1}+\cdots$ ，这是称z_0是f(z)的m级零点。
f(z)以 $z_0$ 为m级零点的充要条件(二选一)
- 在 $z_0$ 点附近，有 $f(z)=(z-z_0)^mg(z)$ ，g(z)在 $z_0$ 解析且 $g(z_0)\neq 0$
- $f(z_0)=f'(z_0)=\cdots=f^{m-1}(z_0)=0$ ，而 $f^{m}(z_0)\neq 0$

形如 $\sum_{n=-\infty}^{+\infty}a_n(z-a)^n=\sum_{n=-\infty}^{-1}a_n(z-a)^n+\sum_{n=0}^{+\infty}a_n(z-a)^n=\sum_{n=1}^{+\infty}a_{-n}(z-a)^{-n}+\sum_{n=0}^{+\infty}a_n(z-a)^n$ 的级数称为洛朗级数
设f(z)在圆环域D: $r < |z-a| < R$ 中解析，则f(z)一定能在这个圆环中展开成洛朗级数，即 $f(z)=\sum_{n=-\infty}^{+\infty}a_n(z-a)^n$ ，其中 $a_n=\frac{1}{2\pi i}\int_c\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta,n=(0,\pm1,\pm2,\cdots)$ ，C是D内围绕a的任意闭路。
设f(z)在点a的某个去心邻域K: $0<|z-a|<R$ 内解析，但在点a不解析，则a称为f(z)的孤立奇点。可等效为内圆收敛到一点的圆环，故f(z)可在K内展开成洛朗级数 $f(z)=\sum_{n=-\infty}^{+\infty}a_n(z-a)^n(0<|z-a|<R)$

$f(z)=a_0+a_1(z-a)+a_2+(z-a)^2+\cdots$ ，称a为f(z)的可去奇点
$f(z)=\frac{a_{-m}}{(z-a)^m}+\cdots+\frac{a_{-1}}{z-a}+\sum_{n=0}^{+\infty}a_n(z-a)^n$ ，称a为f(z)的m级极点
f(z)有无穷多项关于z-a的负次幂，称a为f(z)的本性奇点
a是f(z)的可去奇点的充要条件是：存在某个正数ρ，使得f(z)在环域 $0 < |z-a| < \rho$ 内有界
- $\lim\limits_{z\rightarrow a}f(z)=a_0$
a是f(z)的m级极点充要条件是（二选一）
- $f(z)=\frac{\phi(z)}{(z-a)^m}$ ， $\phi(z)$ 在点解析，且 $\phi(a)\neq 0$ 。
- a是函数 $g(z)=\frac{1}{f(z)}$ 的m极零点
  - $\lim\limits_{z\rightarrow a}f(z)(z-a)^m=\phi(a) \neq0$
  - $\lim\limits_{z\rightarrow a}f(z) = \infty$
a是f(z)的本性奇点的充要条件是不存在有限或无限的极限 $\lim\limits_{z\rightarrow a}f(z)$
如果f(z)在 $\infty$ 点某邻域（即 $R<|z|<+\infty$ ）内解析，则称 $\infty$ 为f(z)的孤立奇点。
- 作代换 $z=\frac{1}{\zeta}$ ，得函数 $\phi(\zeta)=f(\frac{1}{\zeta})$ ，设 $\phi(\zeta)=\sum_{n=-\infty}^{+\infty}a_n\zeta^n$ ，则得到f(z)在无穷远点的邻域展开式为 $f(z)=\sum_{n=\infty}^{+\infty}a_n(\frac{1}{z})^n=\sum_{n=-\infty}^{+\infty}b_nz^n$ ，这里 $b_n=a_{-n}$ 。
$z=\infty$ 是f(z)的可去奇点的充要条件是f(z)的展开式中不含z的正次幂
- $\lim\limits_{z\rightarrow \infty}f(z)=A$
$z=\infty$ 是f(z)的m级极点的充要条件是f(z)的展开式中只有有限个z的正次幂，且最高次幂为m
- $\lim\limits_{z\rightarrow \infty}f(z)=\infty$
$z=\infty$ 是f(z)的本性奇点的充要条件是f(z)的展开式中含无限多各z的正次幂
- $\lim\limits_{z\rightarrow \infty}f(z)$ 不存在

留数及其应用

洛朗展开式中 $a_{-1}$ 称为f(z)在a点的留数或残数
(留数定理) 如果函数f(z)在闭路C上解析，在C的内部除去n个孤立奇点 $a_1,a_2,\cdots,a_n$ 外也解析，则 $\int_cf(z)dz=2\pi i\sum_{k=1}^nRes[f(z),a_k]$
a是f(z)的m级极点，则 $Res[f(z),a]=\frac{1}{(m-1)!}\lim\limits_{z\rightarrow a}\frac{d^{m-1}}{dz^{m-1}}[(z-a)^mf(z)]$
- 设P(z)和Q(z)都在a点解析，且 $P(a)\neq0,Q(a)=0,Q'(a)\neq 0,$ 则 $Res[\frac{P(z)}{Q(z)},a]=\frac{P(a)}{Q'(a)}$

${\color{Red} I=\int_0^{2\pi}R(\sin\theta,\cos\theta)d\theta}$ 型的积分， $R(\sin\theta,\cos\theta)$ 是关于 $\sin\theta,\cos\theta$ 的有理函数。
- 令 $z=e^{i\theta},d\theta=\frac{dz}{iz},\cos\theta=\frac{1}{2}(z+z^{-1}),\sin\theta=\frac{1}{2i}(z-z^{-1})$
- 注：取 $z=e^{ix}$ ,则 $e^{imx}=\cos(mx)+i\sin(mx)=z^m$
(大圆弧引理) 如果当R充分大时，f(z)在圆弧 $C_R:z=Re^{i\theta}$ 上连续，且 $\lim\limits_{z\rightarrow\infty}zf(z)=0$ ,则
- $\lim\limits_{R\rightarrow\infty}\int_{C_R}f(z)dz=0$
(小圆弧引理) 如果当 $\rho$ 充分小时，f(z)在圆弧 $C_{\rho}:z=a+\rho e^{i\theta}(\alpha \leq \theta\leq\beta)$ 上连续，且 $\lim\limits(z-a)f(z)=k$
- 则 $\lim\limits_{\rho\rightarrow0}\int_{C_\rho}f(z)dz=i(\beta-\alpha)k$
(若尔当引理) 如果当R充分大时，g(z)在圆弧 $C_R:\vert z\vert=R,Imz>-a(a>0)$ 上连续，且 $\lim\limits_{z\rightarrow\infty}g(z)=0$ ,则对任何正数 $\lambda$ ,都有 $\lim\limits_{R\rightarrow\infty}\int_{C_R}g(z)e^{i\lambda z}dz=0$
${\color{Red} I=\int_{-\infty}^{+\infty}R(x)dx}$ ，其中 $R(x)=\frac{P(x)}{Q(x)}$ 是有理函数，多项式Q(x)至少比多项式P(x)高2次，且Q(x)实数轴上无零点。
- 则 $\int_{-\infty}^{+\infty}R(x)dx=2\pi i\sum_{k=1}^nRes[R(z),a_k]$ ,其中 $a_1,a_2,\cdots,a_n$ 是f(z)在上半平面内的全部奇点。
${\color{Red} I_1=\int_{-\infty}^{+\infty}R(x)\cos(mx)dx,I_2=\int_{-\infty}^{+\infty}R(x)\sin(mx)dx}$ ,其中 $R(x)=\frac{P(x}{Q(x)}$ 是有理函数，Q(x)至少比P(x)高1次，且Q(x)在实数轴上无零点。
- 则 $\int_{-\infty}^{+\infty}R(x)e^{imx}dx=I_1+iI_2=2\pi i\sum_{k=1}^nRes[R(z)e^{imz},a_k]$ ,其中 $a_1,a_2,\cdots,a_n$ 是复有理函数R(z)上半平面内的全部极点。

设a,b分别是函数f(z)的m级零点和n级极点，则a,b都是 $\frac{f'(z)}{f(z)}$ 的1级极点，且 $Res[\frac{f'(z)}{f(z)},a]=m,Res[\frac{f'(z)}{f(z)},b]=-n$
设f(z)在闭路C上解析且不为零，在C的内部出去有限多个极点外也处处解析，则 $\frac{1}{2\pi i}int_c\frac{f'(z)}{f(z)}dz=N-P$ ,其中N及P分别表示f(z)在C的内部的零点及极点的总数（1个k级零点算k个零点，1个m级极点算m个极点）
(罗歇定理) 设函数f(z)及 $\phi(z)$ 在闭路C及其内部解析，且在C上有不等式， $\vert f(z)\vert > \vert \phi(z)\vert,$ 则在C的内部 $f(z)+\phi(z)$ 和 $f(z)$ 的零点个数相等。

拉普拉斯变换

$L[f(t)]=F(p)=\int_0^{+\infty}f(t)e^{-pt}dt$ 称为函数f(t)的拉普拉斯变换
拉氏变换的存在条件：
- f(t)在t轴上的任何有限区间内逐段光滑
- f(t)是指数增长型的，即存在两个常数 $K>0,c\geq0$ ,使得对所有 $t\geq0$ ，有 $\vert f(t)\vert\leq Ke^{ct}$
拉氏变换后的像函数在 $Rep>c$ 上有意义，是一个解析函数
一些例子

$L[e^{at}]=\frac{1}{p-a}$ ,特别地， $a=0$ 时， $L[1]=\frac{1}{p}$

$L[\cos(wt)]=\frac{p}{p^2+w^2},L[\sin(wt)]=\frac{w}{p^2+w^2},$

$L[\cosh(wt)]=\frac{p}{p^2-w^2},L[\sinh(wt)]=\frac{w}{p^2-w^2}$

(相似定理) $L[f(at)]=\frac{1}{a}F(\frac{p}{a})$
(位移定理) $L[e^{\lambda t}f(t)]=F(p-\lambda)$
$L[e^{\lambda t}\sin(wt)]=\frac{w}{(p-\lambda)^2+w^2},L[e^{\lambda t}\cos(wt)]=\frac{p-\lambda}{(p-\lambda)^2+w^2}$
(像函数微分法) $F'(p)=L[-tf(t)]$ 或 $L[t^nf(t)]=(-1)^nF^{(n)}(p$

$L[t\sin(wt)]=-\frac{d}{dp}(\frac{w}{p^2+w^2})=\frac{2pw}{(p^2+w^2)^2}$

$L[t\cos(wt)]=-\frac{d}{dp}(\frac{p}{p^2+w^2})=\frac{p^2-w^2}{(p^2+w^2)^2}$

$L[t^n]=(-1)^n(\frac{1}{p})^{(n)}=\frac{n!}{p^{n+1}}=\frac{\Gamma(n+1)}{p^{n+1}}$

特别地， $L[\sqrt[]{t}]=\frac{\sqrt[]{\pi}}{2\sqrt[]{p^3}},L[\frac{1}{\sqrt[]{t}}]=\sqrt[]{\frac{\pi}{p}}$

(本函数微分法) $L[f'(t)]=pF(p)-f(+0)$
- $L[f^{(n)}(t)]=p^nL[f(t)]-p^{n-1}f(+0)-p^{n-2}f'(+0)-\cdots-pf^{(n-2)}(+0)-f^{(n-1)}(+0)$
(本函数积分法) $L[\int_0^tf(t)dt]=\frac{F(p)}{p}$
(延迟定理) $L[f(t-\tau)]=e^{-p\tau}F(p)$
(卷积定理) $L[f*g]=F(p)G(p),f*g=\int_{-\infty}^{+\infty}f(x-\epsilon)g(\epsilon)d\epsilon$
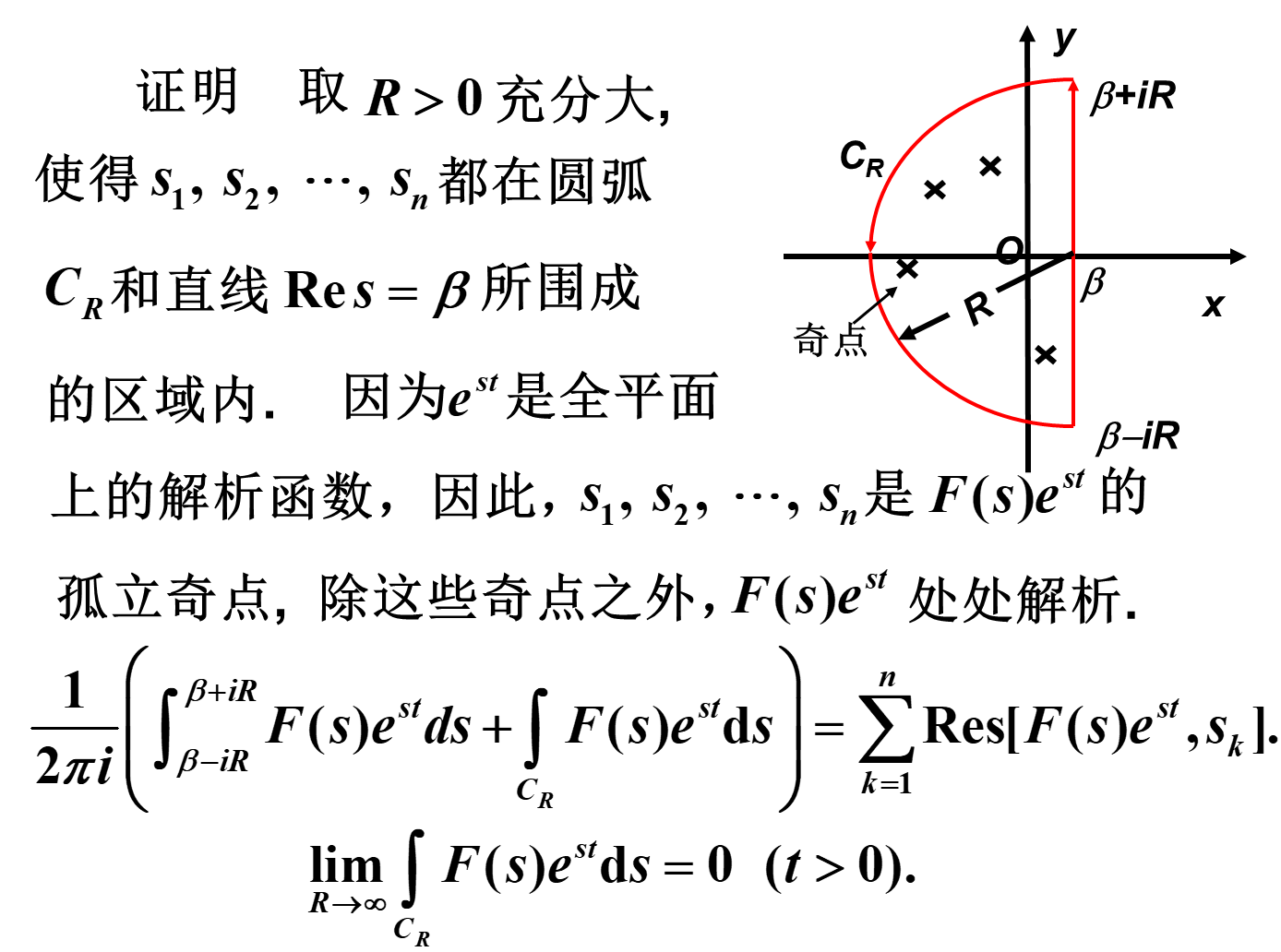
设F(p)除在左半平面 $Rep<\sigma(\sigma >c)$ 内有奇点 $p_1,p_2,\cdots,p_n$ 外在p平面内处处解析，且 $\lim\limits_{p\rightarrow \infty}F(p)=0$ ，则 $f(t)=\sum_{k=1}^nRes[F(p)e^{pt},p_k]$