本文主要是介绍【复变函数笔记】傅里叶变换和拉普拉斯变换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、傅里叶变换和拉普拉斯变换的定义
- 1. 傅里叶积分
- 2. 傅里叶变换
- 3. 单位脉冲函数和单位阶跃函数
- 4. 拉普拉斯变换
- 二、常见函数的傅里叶变换和拉普拉斯变换
- 三、傅里叶变换和拉普拉斯变换的性质
- 四、拉普拉斯逆变换
一、傅里叶变换和拉普拉斯变换的定义
1. 傅里叶积分
傅里叶积分定理 若 f ( t ) f(t) f(t)在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)上满足下列条件:
(1) f ( t ) f(t) f(t)在任一有限区间上满足狄利克雷条件(连续或只有有限个第一类间断点;只有有限个极值点);
(2) f ( t ) f(t) f(t)在无限区间 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)上绝对可积(即积分 ∫ − ∞ + ∞ ∣ f ( t ) ∣ d t \int_{-\infty}^{+\infty}|f(t)|\mathrm{d}t ∫−∞+∞∣f(t)∣dt收敛),则有 f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − i ω τ d τ ] e i ω t d ω f(t)=\frac{1}{2\pi }\int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty} f(\tau)e^{-i\omega\tau}\mathrm{d}\tau\right]e^{i\omega t}\mathrm{d}\omega f(t)=2π1∫−∞+∞[∫−∞+∞f(τ)e−iωτdτ]eiωtdω成立,而左端的 f ( t ) f(t) f(t)在其间断点处应以 f ( t + 0 ) + f ( t − 0 ) 2 \frac{f(t+0)+f(t-0)}{2} 2f(t+0)+f(t−0)(左右极限平均值)代替。
2. 傅里叶变换
傅里叶变换:若 f ( t ) f(t) f(t)在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)上满足傅里叶积分的条件,则称函数 F ( ω ) = F [ f ( t ) ] = ∫ − ∞ + ∞ f ( t ) e − i ω t d t F(\omega)=\mathscr{F}[f(t)]=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}\mathrm{d}t F(ω)=F[f(t)]=∫−∞+∞f(t)e−iωtdt为 f ( t ) f(t) f(t)的傅里叶变换;而称函数 f ( t ) = F − 1 [ F ( ω ) ] = 1 2 π ∫ − ∞ + ∞ F ( ω ) e i ω t d ω f(t)=\mathscr{F}^{-1}[F(\omega)]=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}\mathrm{d}\omega f(t)=F−1[F(ω)]=2π1∫−∞+∞F(ω)eiωtdω为 F ( ω ) F(\omega) F(ω)的傅里叶逆变换。
3. 单位脉冲函数和单位阶跃函数
单位脉冲函数: δ ( t ) = { + ∞ , t = 0 0 , t ≠ 0 \delta(t)=\begin{cases} +\infty,&t=0\\ 0,&t\ne 0 \end{cases} δ(t)={+∞,0,t=0t=0这是一个不严谨的表述,严谨的表述需要用到弱极限。该函数满足 ∫ − ∞ + ∞ δ ( t ) d t = 1 \int_{-\infty}^{+\infty}\delta(t)\mathrm{d}t=1 ∫−∞+∞δ(t)dt=1若 f ( t ) f(t) f(t)为无穷次可微的函数,则有 ∫ − ∞ + ∞ δ ( t ) f ( t ) d t = f ( 0 ) \int_{-\infty}^{+\infty}\delta(t)f(t)\mathrm{d}t=f(0) ∫−∞+∞δ(t)f(t)dt=f(0) δ ( t ) \delta(t) δ(t)是偶函数,满足 δ ( a t ) = 1 ∣ a ∣ δ ( t ) \delta(at)=\frac{1}{|a|}\delta(t) δ(at)=∣a∣1δ(t)( a ≠ 0 a\ne 0 a=0),且 ∫ − ∞ + ∞ δ ( n ) ( t − t 0 ) f ( t ) d t = ( − 1 ) n f ( n ) ( t 0 ) \int_{-\infty}^{+\infty}\delta^{(n)}(t-t_0)f(t)\mathrm{d}t={(-1)}^n f^{(n)}(t_0) ∫−∞+∞δ(n)(t−t0)f(t)dt=(−1)nf(n)(t0)(这个用分部积分证明)。特别地, ∫ − ∞ + ∞ δ ′ ( t ) f ( t ) d t = − f ′ ( 0 ) \int_{-\infty}^{+\infty}\delta'(t)f(t)\mathrm{d}t=-f'(0) ∫−∞+∞δ′(t)f(t)dt=−f′(0)
单位阶跃函数: u ( t ) = { 1 , t > 0 0 , t < 0 u(t)=\begin{cases} 1,&t>0\\ 0,&t<0 \end{cases} u(t)={1,0,t>0t<0满足 ∫ − ∞ t δ ( τ ) d τ = u ( t ) d d t u ( t ) = δ ( t ) \int_{-\infty}^t\delta(\tau)\mathrm{d}\tau=u(t)\\ \frac{\mathrm{d}}{\mathrm{d}t}u(t)=\delta(t) ∫−∞tδ(τ)dτ=u(t)dtdu(t)=δ(t)
4. 拉普拉斯变换
拉普拉斯变换:设函数 f ( t ) f(t) f(t)在 t ≥ 0 t\ge 0 t≥0时有定义,且积分 ∫ 0 + ∞ f ( t ) e − s t d t \int_0^{+\infty}f(t)e^{-st}\mathrm{d}t ∫0+∞f(t)e−stdt在复平面 s s s的某一区域内收敛,则称 F ( s ) = L [ f ( t ) ] = ∫ 0 + ∞ f ( t ) e − s t d t F(s)=\mathscr{L}[f(t)]=\int_0^{+\infty}f(t)e^{-st}\mathrm{d}t F(s)=L[f(t)]=∫0+∞f(t)e−stdt为 f ( t ) f(t) f(t)的拉普拉斯变换(或称为象函数),称 f ( t ) f(t) f(t)为 F ( s ) F(s) F(s)的拉普拉斯逆变换(或称为象原函数),记为 f ( t ) = L − 1 [ F ( s ) ] f(t)=\mathscr{L}^{-1}[F(s)] f(t)=L−1[F(s)]若令 s = β + i ω s=\beta+i\omega s=β+iω,则 L [ f ( t ) ] = F [ f ( t ) u ( t ) e − β t ] \mathscr{L}[f(t)]=\mathscr{F}[f(t)u(t)e^{-\beta t}] L[f(t)]=F[f(t)u(t)e−βt]。这就是拉普拉斯变换和傅里叶变换的关系。
拉普拉斯变换的存在定理 若函数 f ( t ) f(t) f(t)满足下列条件:
(1) 在 t ≥ 0 t\ge 0 t≥0的任一有限区间上连续或分段连续;
(2) 当 t → + ∞ t\to+\infty t→+∞时, f ( t ) f(t) f(t)的增长速度不超过某一指数函数,即存在 M > 0 M>0 M>0和 c ≥ 0 c\ge 0 c≥0使得 ∣ f ( t ) ∣ ≤ M e c t , ∀ t ∈ [ 0 , + ∞ ) |f(t)|\le Me^{ct},\forall t\in[0,+\infty) ∣f(t)∣≤Mect,∀t∈[0,+∞)则 f ( t ) f(t) f(t)的拉普拉斯变换 F ( s ) = ∫ 0 + ∞ f ( t ) e − s t d t F(s)=\int_0^{+\infty}f(t)e^{-st}\mathrm{d}t F(s)=∫0+∞f(t)e−stdt在半平面 Re ( s ) > c \operatorname{Re}(s)>c Re(s)>c上一定存在,右端的积分在 Re ( s ) ≥ c 1 > c \operatorname{Re}(s)\ge c_1>c Re(s)≥c1>c上绝对收敛而且一致收敛,并且在 Re ( s ) > c \operatorname{Re}(s)>c Re(s)>c的半平面内, F ( s ) F(s) F(s)为解析函数。 c c c称为 f ( t ) f(t) f(t)的增长指数。
二、常见函数的傅里叶变换和拉普拉斯变换
| 象原函数 f ( t ) f(t) f(t) | 傅里叶变换 | 拉普拉斯变换 |
|---|---|---|
| 1 1 1 | 2 π δ ( ω ) 2\pi\delta(\omega) 2πδ(ω) | - |
| δ ( t ) \delta(t) δ(t) | 1 1 1 | 1 1 1 |
| u ( t ) u(t) u(t) | 1 i ω + π δ ( ω ) \cfrac{1}{i\omega}+\pi\delta(\omega) iω1+πδ(ω) | 1 s \cfrac{1}{s} s1 |
| t n t^n tn | 2 π i n δ ( n ) ( ω ) 2\pi i^n\delta^{(n)}(\omega) 2πinδ(n)(ω) | Γ ( n + 1 ) s ( n + 1 ) ( n > − 1 ) \cfrac{\Gamma(n+1)}{s^{(n+1)}}(n>-1) s(n+1)Γ(n+1)(n>−1)(当 n n n为整数时为 n ! s n + 1 \cfrac{n!}{s^{n+1}} sn+1n!) |
| cos ω 0 t \cos\omega_0 t cosω0t | π [ δ ( ω + ω 0 ) + δ ( ω − ω 0 ) ] \pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)] π[δ(ω+ω0)+δ(ω−ω0)] | s s 2 + ω 0 2 \cfrac{s}{s^2+\omega_0^2} s2+ω02s(要求 ω 0 ∈ R \omega_0\in\mathbb{R} ω0∈R) |
| sin ω 0 t \sin\omega_0 t sinω0t | i π [ δ ( ω + ω 0 ) − δ ( ω − ω 0 ) ] i\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)] iπ[δ(ω+ω0)−δ(ω−ω0)] | ω 0 s 2 + ω 0 2 \cfrac{\omega_0}{s^2+\omega_0^2} s2+ω02ω0(要求 ω 0 ∈ R \omega_0\in\mathbb{R} ω0∈R) |
| e − β t u ( t ) e^{-\beta t}u(t) e−βtu(t) | 1 β + i ω ( β > 0 ) \cfrac{1}{\beta+i\omega}(\beta>0) β+iω1(β>0) | 1 s + β \cfrac{1}{s+\beta} s+β1 |
三、傅里叶变换和拉普拉斯变换的性质
令 F ( ω ) = F [ f ( t ) ] F(\omega)=\mathscr{F}[f(t)] F(ω)=F[f(t)], F ( s ) = L [ f ( t ) ] F(s)=\mathscr{L}[f(t)] F(s)=L[f(t)]。
| 性质 | 傅里叶变换 | 拉普拉斯变换 |
|---|---|---|
| 线性性质 | F [ a f 1 ( t ) + b f 2 ( t ) ] = a F [ f 1 ( t ) ] + b F [ f 2 ( t ) ] \mathscr{F}[af_1(t)+bf_2(t)]=a\mathscr{F}[f_1(t)]+b\mathscr{F}[f_2(t)] F[af1(t)+bf2(t)]=aF[f1(t)]+bF[f2(t)] | L [ a f 1 ( t ) + b f 2 ( t ) ] = a L [ f 1 ( t ) ] + b L [ f 2 ( t ) ] \mathscr{L}[af_1(t)+bf_2(t)]=a\mathscr{L}[f_1(t)]+b\mathscr{L}[f_2(t)] L[af1(t)+bf2(t)]=aL[f1(t)]+bL[f2(t)] |
| 相似性质 | F [ f ( a t ) ] = 1 ∣ a ∣ F ( ω a ) \mathscr{F}[f(at)]=\frac{1}{|a|}F\left(\frac{\omega}{a}\right) F[f(at)]=∣a∣1F(aω) | L [ f ( a t ) ] = 1 a F ( s a ) \mathscr{L}[f(at)]=\frac{1}{a}F\left(\frac{s}{a}\right) L[f(at)]=a1F(as)( a > 0 a>0 a>0) |
| 对称性质 | F [ F ( ω ) ] = 2 π f ( − t ) \mathscr{F}[F(\omega)]=2\pi f(-t) F[F(ω)]=2πf(−t) | |
| 微分性质 | F [ f ′ ( t ) ] = i ω F [ f ( t ) ] \mathscr{F}[f'(t)]=i\omega\mathscr{F}[f(t)] F[f′(t)]=iωF[f(t)] F [ f ( n ) ( t ) ] = ( i ω ) n F [ f ( t ) ] \mathscr{F}[f^{(n)}(t)]={(i\omega)}^n\mathscr{F}[f(t)] F[f(n)(t)]=(iω)nF[f(t)] | L [ f ′ ( t ) ] = s F ( s ) − f ( 0 ) \mathscr{L}[f'(t)]=sF(s)-f(0) L[f′(t)]=sF(s)−f(0) L [ f ( n ) ( t ) ] = s n F ( s ) − s n − 1 f ( 0 ) − ⋯ − f ( n − 1 ) ( 0 ) \mathscr{L}[f^{(n)}(t)]=s^n F(s)-s^{n-1}f(0)-\cdots-f^{(n-1)}(0) L[f(n)(t)]=snF(s)−sn−1f(0)−⋯−f(n−1)(0) |
| 象函数的微分性质 | F [ t f ( t ) ] = i F ′ ( ω ) \mathscr{F}[tf(t)]=iF'(\omega) F[tf(t)]=iF′(ω) F [ t n f ( t ) ] = i n F ( n ) ( ω ) \mathscr{F}[t^n f(t)]=i^n F^{(n)}(\omega) F[tnf(t)]=inF(n)(ω) | L [ t f ( t ) ] = − F ′ ( s ) \mathscr{L}[tf(t)]=-F'(s) L[tf(t)]=−F′(s) L [ t n f ( t ) ] = ( − 1 ) n F ( n ) ( s ) \mathscr{L}[t^n f(t)]={(-1)}^n F^{(n)}(s) L[tnf(t)]=(−1)nF(n)(s) |
| 位移性质 | F [ f ( t + t 0 ) ] = e i ω t 0 F [ f ( t ) ] \mathscr{F}[f(t+t_0)]=e^{i\omega t_0}\mathscr{F}[f(t)] F[f(t+t0)]=eiωt0F[f(t)] | L [ f ( t + t 0 ) ] = e s t 0 L [ f ( t ) ] \mathscr{L}[f(t+t_0)]=e^{st_0}\mathscr{L}[f(t)] L[f(t+t0)]=est0L[f(t)](要求 t 0 < 0 t_0<0 t0<0) |
| 象函数的位移性质 | F [ e i ω 0 t f ( t ) ] = F ( ω − ω 0 ) \mathscr{F}[e^{i\omega_0 t}f(t)]=F(\omega-\omega_0) F[eiω0tf(t)]=F(ω−ω0) | L [ e a t f ( t ) ] = F ( s − a ) \mathscr{L}[e^{at}f(t)]=F(s-a) L[eatf(t)]=F(s−a)(要求 Re ( s − a ) > s 0 \operatorname{Re}(s-a)>s_0 Re(s−a)>s0,其中 s 0 s_0 s0是 f ( t ) f(t) f(t)的增长指数) |
| 积分性质 | F [ ∫ − ∞ t f ( τ ) d τ ] = 1 i ω F ( ω ) + π F ( 0 ) δ ( ω ) \mathscr{F}\left[\int_{-\infty}^t f(\tau)\mathrm{d}\tau\right]=\frac{1}{i\omega}F(\omega)+\pi F(0)\delta(\omega) F[∫−∞tf(τ)dτ]=iω1F(ω)+πF(0)δ(ω) | L [ ∫ 0 t f ( τ ) d τ ] = 1 s F ( s ) \mathscr{L}[\int_0^t f(\tau)\mathrm{d}\tau]=\frac{1}{s}F(s) L[∫0tf(τ)dτ]=s1F(s) |
| 象函数的积分性质 | L [ f ( t ) t ] = ∫ s ∞ F ( s ) d s \mathscr{L}\left[\frac{f(t)}{t}\right]=\int_s^\infty F(s)\mathrm{d}s L[tf(t)]=∫s∞F(s)ds | |
| 卷积定理 | F [ f 1 ( t ) ∗ f 2 ( t ) ] = F [ f 1 ( t ) ] ⋅ F [ f 2 ( t ) ] \mathscr{F}[f_1(t)*f_2(t)]=\mathscr{F}[f_1(t)]\cdot\mathscr{F}[f_2(t)] F[f1(t)∗f2(t)]=F[f1(t)]⋅F[f2(t)] F [ f 1 ( t ) ⋅ f 2 ( t ) ] = 1 2 π F [ f 1 ( t ) ] ∗ F [ f 2 ( t ) ] \mathscr{F}[f_1(t)\cdot f_2(t)]=\frac{1}{2\pi}\mathscr{F}[f_1(t)]*\mathscr{F}[f_2(t)] F[f1(t)⋅f2(t)]=2π1F[f1(t)]∗F[f2(t)] | L [ f 1 ( t ) ∗ f 2 ( t ) ] = L [ f 1 ( t ) ] ⋅ L [ f 2 ( t ) ] \mathscr{L}[f_1(t)*f_2(t)]=\mathscr{L}[f_1(t)]\cdot\mathscr{L}[f_2(t)] L[f1(t)∗f2(t)]=L[f1(t)]⋅L[f2(t)] |
| 乘积定理 | 令 F 1 ( ω ) = F [ f 1 ( t ) ] F_1(\omega)=\mathscr{F}[f_1(t)] F1(ω)=F[f1(t)], F 2 ( ω ) = F [ f 2 ( t ) ] F_2(\omega)=\mathscr{F}[f_2(t)] F2(ω)=F[f2(t)],则 ∫ − ∞ + ∞ f 1 ( t ) ‾ f 2 ( t ) d t = 1 2 π ∫ − ∞ + ∞ F 1 ( ω ) ‾ F 2 ( ω ) d ω \int_{-\infty}^{+\infty}\overline{f_1(t)}f_2(t)\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\overline{F_1(\omega)}F_2(\omega)\mathrm{d}\omega ∫−∞+∞f1(t)f2(t)dt=2π1∫−∞+∞F1(ω)F2(ω)dω ∫ − ∞ + ∞ f 1 ( t ) f 2 ( t ) ‾ d t = 1 2 π ∫ − ∞ + ∞ F 1 ( ω ) F 2 ( ω ) ‾ d ω \int_{-\infty}^{+\infty}f_1(t)\overline{f_2(t)}\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F_1(\omega)\overline{F_2(\omega)}\mathrm{d}\omega ∫−∞+∞f1(t)f2(t)dt=2π1∫−∞+∞F1(ω)F2(ω)dω | |
| 能量积分 | 帕西瓦尔等式: ∫ − ∞ + ∞ [ f ( t ) ] 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ F ( ω ) ∣ 2 d ω \int_{-\infty}^{+\infty}{[f(t)]}^2\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{|F(\omega)|}^2\mathrm{d}\omega ∫−∞+∞[f(t)]2dt=2π1∫−∞+∞∣F(ω)∣2dω | |
| 初值定理 | f ( 0 ) = lim s → ∞ s F ( s ) f(0)=\lim\limits_{s\to\infty}sF(s) f(0)=s→∞limsF(s)(若这个极限存在) | |
| 终值定理 | lim t → + ∞ f ( t ) = lim s → 0 s F ( s ) \lim\limits_{t\to+\infty}f(t)=\lim\limits_{s\to 0}sF(s) t→+∞limf(t)=s→0limsF(s) (要求 s F ( s ) sF(s) sF(s)的所有奇点都在 s s s平面的左半部) |
四、拉普拉斯逆变换
由于 F ( s ) = L [ f ( t ) ] = F [ f ( t ) u ( t ) e − β t ] F(s)=\mathscr{L}[f(t)]=\mathscr{F}[f(t)u(t)e^{-\beta t}] F(s)=L[f(t)]=F[f(t)u(t)e−βt]( s = β + i ω s=\beta+i\omega s=β+iω),我们有 1 2 π ∫ − ∞ + ∞ F ( β + i ω ) e i ω t d ω = f ( t ) u ( t ) e − β t f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( β + i ω ) e ( β + i ω ) t d ω \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\beta+i\omega)e^{i\omega t}\mathrm{d}\omega=f(t)u(t)e^{-\beta t}\\ f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\beta+i\omega)e^{(\beta+i\omega)t}\mathrm{d}\omega 2π1∫−∞+∞F(β+iω)eiωtdω=f(t)u(t)e−βtf(t)=2π1∫−∞+∞F(β+iω)e(β+iω)tdω注意到 d s = i d ω \mathrm{d}s=i\mathrm{d}\omega ds=idω,我们把积分写出复变函数的积分: f ( t ) = 1 2 π i ∫ β − i ∞ β + i ∞ F ( s ) e s t d s f(t)=\frac{1}{2\pi i}\int_{\beta-i\infty}^{\beta+i\infty}F(s)e^{st}\mathrm{d}s f(t)=2πi1∫β−i∞β+i∞F(s)estds下面我们通过留数来计算这个积分。
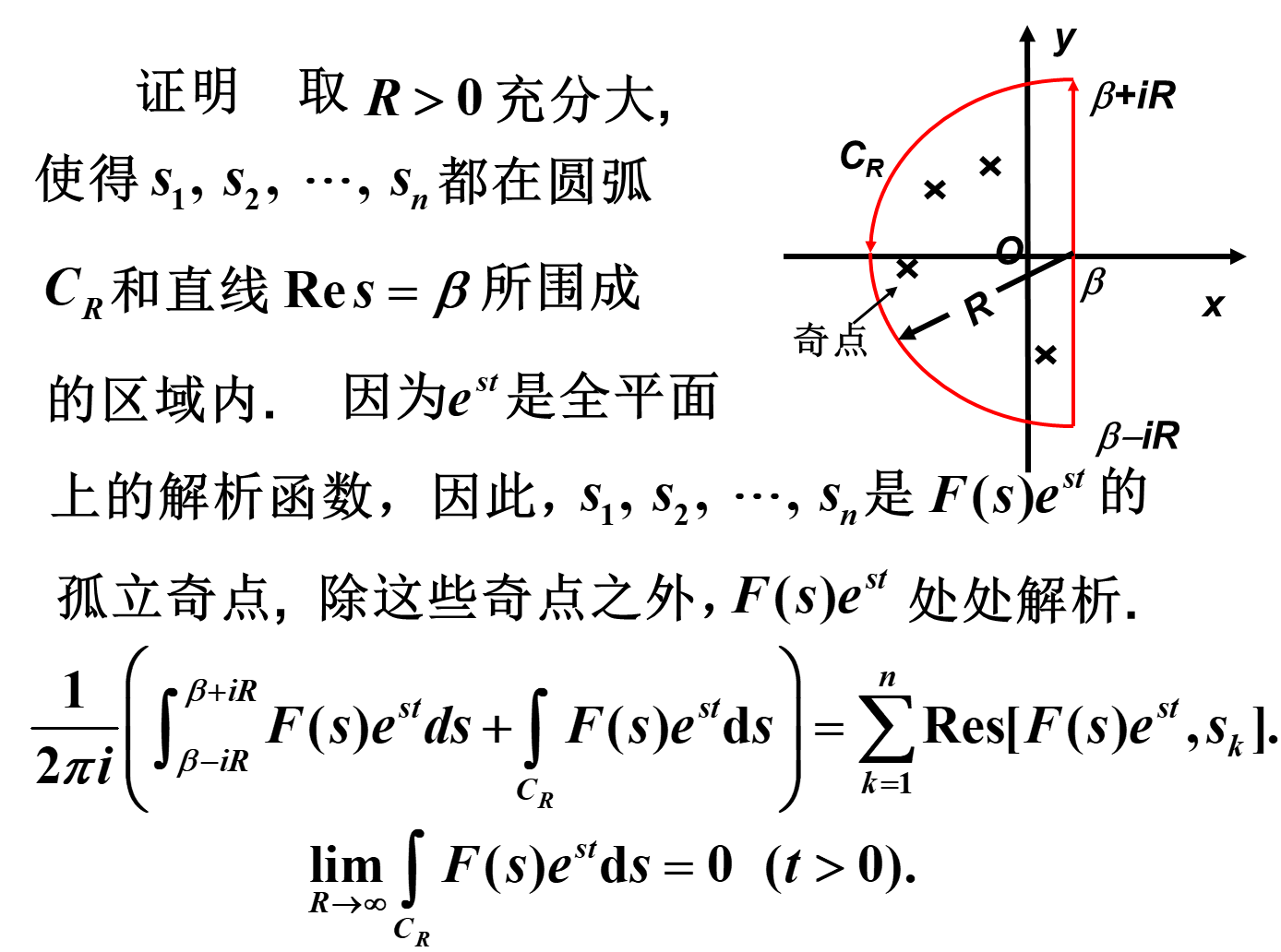
定理 设 s 1 , s 2 , ⋯ , s l s_1,s_2,\cdots,s_l s1,s2,⋯,sl是 F ( s ) F(s) F(s)的所有孤立奇点(有限个),除这些点外, F ( s ) F(s) F(s)处处解析。且存在 R 0 > 0 R_0>0 R0>0,使得当 ∣ s ∣ > R 0 |s|>R_0 ∣s∣>R0时, ∣ F ( s ) ∣ ≤ M ( r ) |F(s)|\le M(r) ∣F(s)∣≤M(r),其中 M ( r ) M(r) M(r)是 r r r的实函数,满足 lim r → + ∞ M ( r ) = 0 \lim\limits_{r\to+\infty}M(r)=0 r→+∞limM(r)=0(即当 s → ∞ s\to\infty s→∞时, F ( s ) → 0 F(s)\to 0 F(s)→0)。选取 β \beta β,使所有孤立奇点的实部都小于 β \beta β,则当 t > 0 t>0 t>0时, f ( t ) = 1 2 π i ∫ β − i ∞ β + i ∞ F ( s ) e s t d s = ∑ k = 1 l Res [ F ( s ) e s t , s k ] f(t)=\frac{1}{2\pi i}\int_{\beta-i\infty}^{\beta+i\infty}F(s)e^{st}\mathrm{d}s=\sum\limits_{k=1}^l \operatorname{Res}[F(s)e^{st},s_k] f(t)=2πi1∫β−i∞β+i∞F(s)estds=k=1∑lRes[F(s)est,sk]
这篇关于【复变函数笔记】傅里叶变换和拉普拉斯变换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


