本文主要是介绍通信入门系列——复变函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本节目录
一、复变函数
1、复数
2、复数的四则运算
二、复指数函数
三、欧拉公式
本节内容
一、复变函数
1、复数
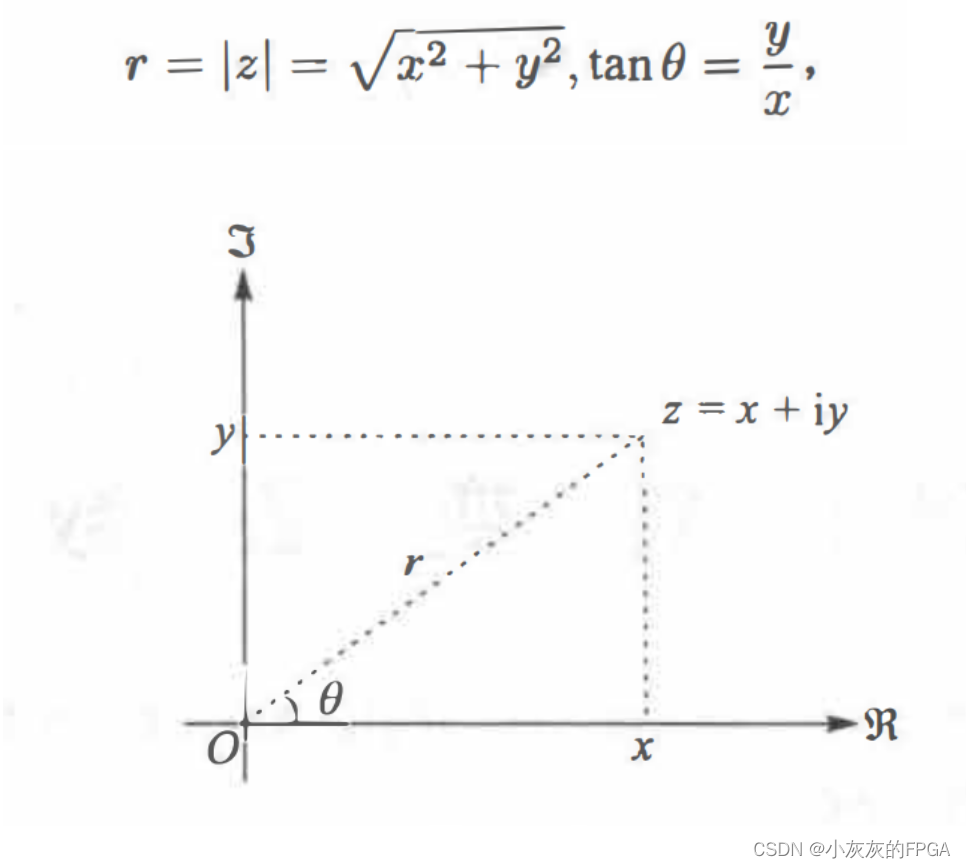
复数单位i,也就是满足i^2=-1,将z=x+iy表示为复数z,x和y为任意的实数,称为复数z的实部和虚部。由复数z=x+iy对应的点(x,y)组成的二维平面,称为复平面,也叫作高斯平面。复平面上的点,可以用模和幅度角来进行表示,横坐标为实部,纵坐标为虚部,r表示复数的模,θ表示幅角。
2、复数的四则运算
复数的四则运算,和实数加减乘除大致相同,需要注意的是复数的乘法核除法。对于复数的加减法来说,只需要将实部和虚部分布加减即可。
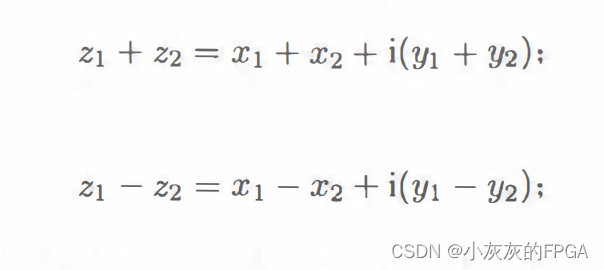
复数的乘法运算,遵循多项式乘法,同时将i^2=-1应用都计算中,即:
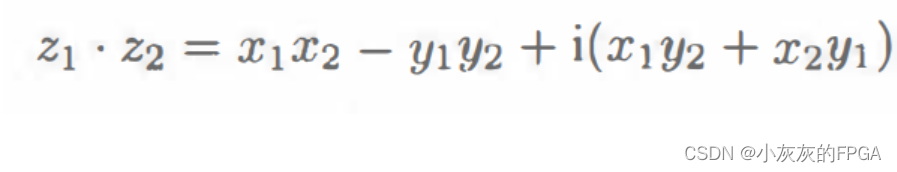
复数的除法运算,需要引入共轭复数,z=x+iy的共轭复数为x-iy。
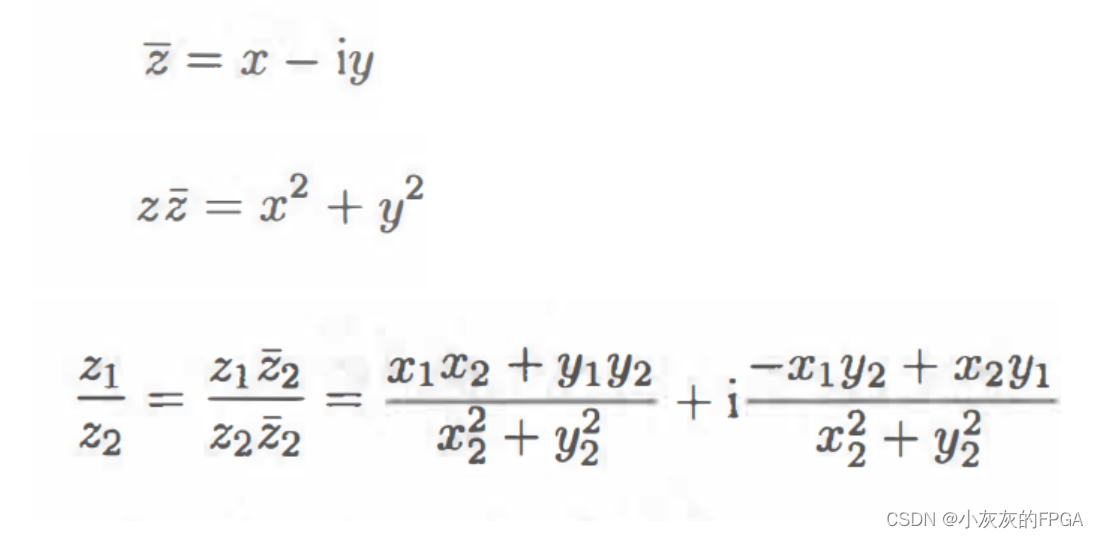
二、复指数函数
以复数z=x+iy为自变量的函数称为复变函数,当然,在通信中,最常用的复变函数是复指数函数,以自然对数e为底的函数,f(z)=ez=e(x=iy)。其实e^x函数可以通过麦克劳林级数展开为:
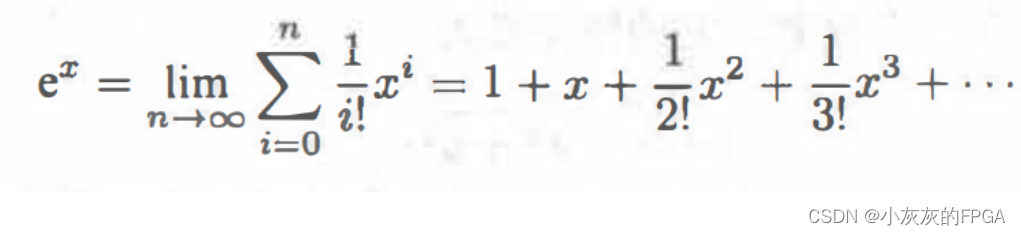
复数数列的极限:设{xn}为一个复数列,A为一个给定的复数。若对于任意给定的实数ε>0,总存在正整数N,使得当n>N时有|xn-A|<ε,那么称数列{xn}收敛于A,定复数A称为数列{xn}的极限。
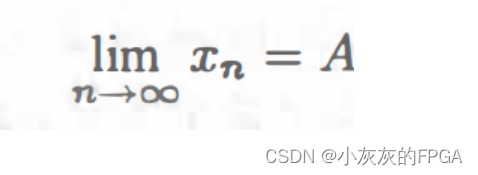
两个复数之间的距离:在复数域中|z|表示的是模的概念,两个复数之间差值的模表示的就是这两个复平面对应的点之间距离。假设z1=x1+iy1,z2=x2+iy2,对z1和z2对应的点之间的距离为|z1-z2|,即:
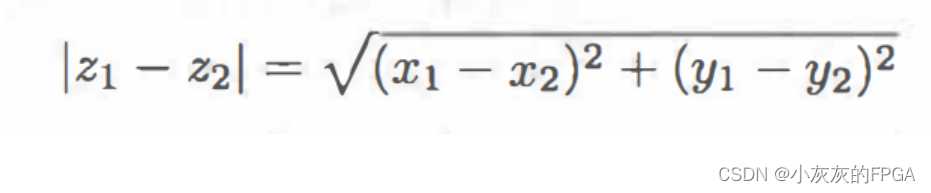
复指数函数:复数z=x+iy,则复指数函数为:
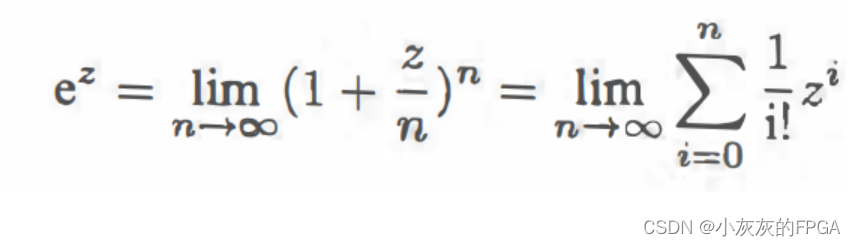
三、欧拉公式
欧拉公式满足e ^ (ix)=cosx+isinx。当然将其扩大到复数,那么三角函数和指数函数之间就存在一定的关系。将x=π,也就是e ^ (iπ)+1=0。
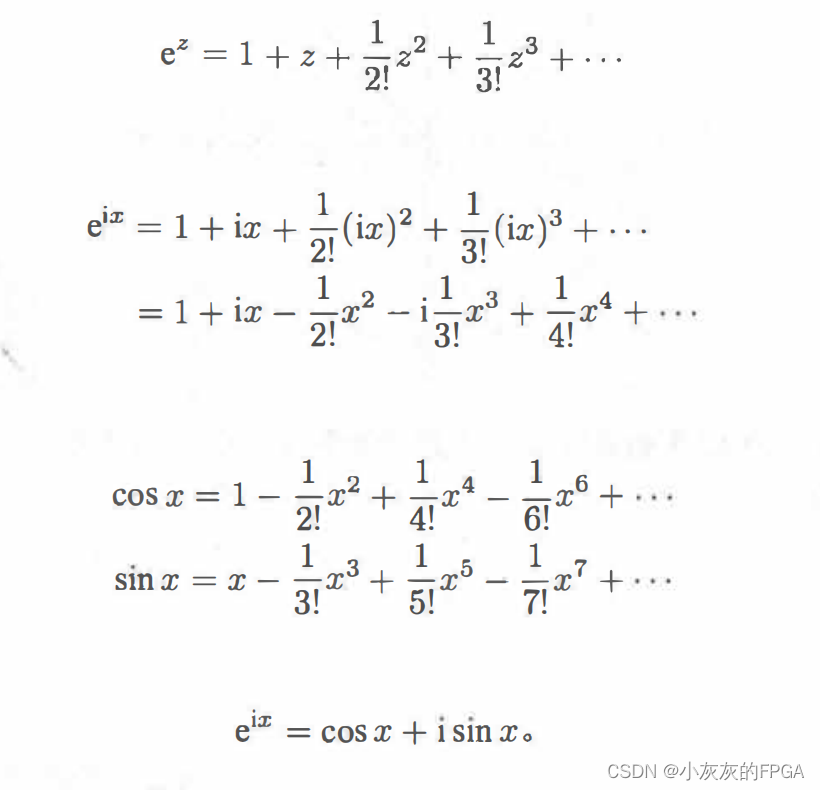
欧拉公式表示复指数函数与三角函数之间的关系变换,令z=e ^ (ix),那么复指数函数,就可以用z=r×e ^ (iθ)来表示你,其中r表示复数的模,θ表示幅角,计算关系式如下:

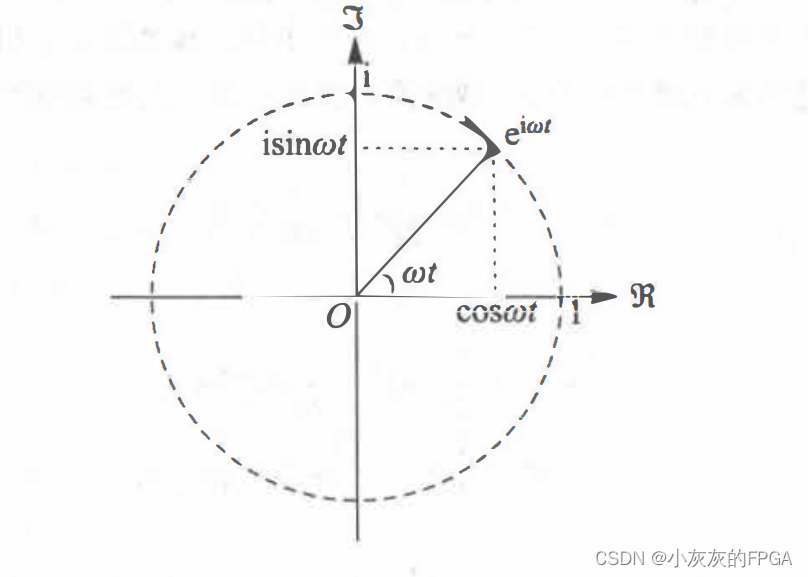
在通信中,引入了角速度ω的概念,来表述复指数信号,表达式为:e ^ (iωt)=cosωt+isinωt,其中cosωt余弦信号为实部,sinωt正弦信号为虚部,可以理解为一个点在复平面的单位圆上,以角速度ω逆时针运动,具体如图所示:
这篇关于通信入门系列——复变函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






