圆周率专题
【matlab 圆周率计算】matlab 求圆周率的两种算法实现比较
%author:laidefa %data:2014-09-19 %丘德诺夫斯基公式求圆周率 function mpi=qdnfsj(m) i=m; s=13591409; for n=1:i A=(factorial(6n)(13591409+54514013n))/(factorial(3n)factorial(n)3*(-640320)(3n)); s=s+A; end mpi=(42688
蒙特卡洛模拟计算圆周率和积分
蒙特卡洛模拟计算圆周率 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib.patches import Circlen = 1000r = 1.0a,b = (0.0,0.0)xmin,xmax = a-r,a+rymin,ymax = b-r,b+rx = np.
蒙特卡洛方法近似计算圆周率
一、原理图 正方形区域内有1/4圆区域,向区域内随机大量掷点。根据概率论知识,落在每一点的概率相等,当n无限大时,落在1/4区域内的点占总点数量的比例即1/4圆占正方形面积的比例,圆周率PI=4(N1/N)[N1:落在1/4圆中点的数量,N:总点数]。 二、c++试验 #include <iostream>#include <random>#include <cmath>#i
C++ 圆周率的几种求解方法
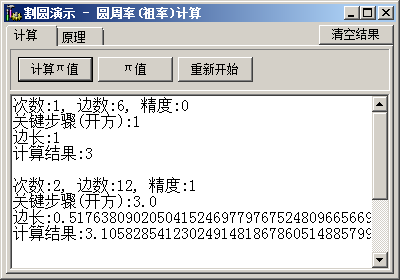
公众号:编程驿站 圆周率的常见几种求解算法,包括但不仅仅包含特卡洛模拟、割圆法和公式法。本文讲解这几种算法的实现流程。 1. 蒙特卡洛模拟算法 假设有一个半径为1的圆,如图所示。先绘制一个半径为1的圆。则图中阴影部分(1/4圆)的面积就等于π/4。 再绘制出一个正方形,可以看出它的面积是 1 。通过这种方式,就能够获取到正方形面积和阴影部分面积的一个比例。如此可得到正方形和阴影面积的比
java蓝桥杯练习-圆周率与级数
我国古代数学家对圆周率方面的研究工作,成绩是突出的。三国时期的刘徽、南北朝时期的祖冲之都在这个领域取得过辉煌战绩。 有了计算机,圆周率的计算变得十分容易了。如今,人们创造了上百种方法求π的值。其中比较常用且易于编程的是无穷级数法。 π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 - … 是初学者特别喜欢的一个级数形式,但其缺点是收敛太慢。 π/2 = 1 + 1/3 +1/32/5
数学分析复习:圆周率和 Euler 常数的构造
文章目录 圆周率 π \pi π 和 Euler 常数 e e e 的构造圆周率 π \pi π 的构造Euler常数e的构造 本篇文章适合个人复习翻阅,不建议新手入门使用 圆周率 π \pi π 和 Euler 常数 e e e 的构造 圆周率 π \pi π 的构造 我们将以下数列的极限定义为 π \pi π L n = n ⋅ sin 18 0
使用布丰投针法精确计算圆周率
如果在平面上有两条距离为d的平行线,假设如果拿一根长度是L的铁针随机的丢到纸面上去,那么试问铁针与某条直线所相交的概率是多少,假设铁针的长度L是大于平行线的距离d的,这样铁针就不会同时与两条直线所相交了。 添加图片注释,不超过 140 字(可选) 对于所给的问题,假设x是铁针中点与距离最近的那条平行线之间的距离,同时a是针与线形成的夹角,由此就可以使用这两个变量来描述针是否与线产生了相
圆周率小数点后1024热位图
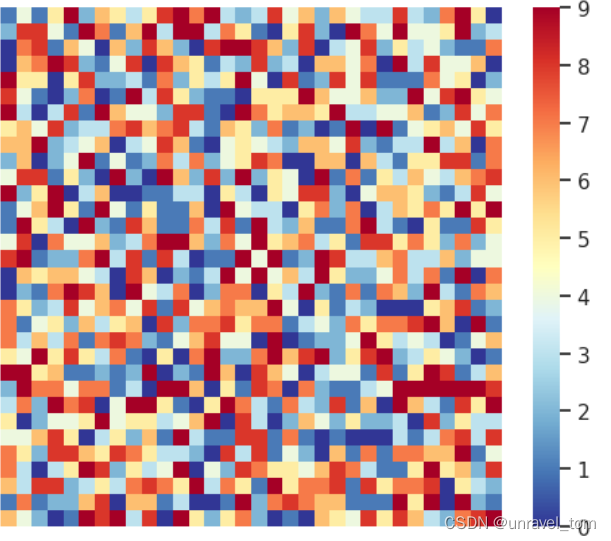
前言 使用的python IDE :Jupyter (在Anaconda中打开Anaconda notebook打开,没有进行第三方的库和模块的下载) import numpy as npfrom mpmath import mpimport seaborn as snsimport matplotlib.pyplot as pltimport pandas as pd#取pi的102
运行hadoop自带计算圆周率例子操作
运行hadoop自带计算圆周率的jar 1、进入到hadoop安装位置,本人位置为:/usr/centos/hadoop。 2、进入handoop后找到share文件夹,并如图: 3、进入share/hadoop/mapreduce文件夹,找到hadoop-mapreduce-examples-3.2.0.jar(不同hadoop版本名字中数字部分不同)。 4、运行jar包:hadoo
MATLAB练习题:利用蒙特卡罗模拟来计算圆周率π
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 蒙特卡罗模拟是一种以概率和统计理论为基础的计算方法,它能通过随机数来解决很多计算问题。蒙特卡罗模拟将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。本题将利用蒙特卡
35.蓝桥杯之圆周率与级数
我国古代数学家对圆周率方面的研究工作,成绩是突出的。三国时期的刘徽、南北朝时期的祖冲之都在这个领域取得过辉煌战绩。 有了计算机,圆周率的计算变得十分容易了。如今,人们创造了上百种方法求π的值。其中比较常用且易于编程的是无穷级数法。 π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 - … 是初学者特别喜欢的一个级数形式,但其缺点是收敛太慢。 π/2 = 1 + 1/3 +1/32/5
圆周率的计算(C语言版,绝对精华)
#include<stdio.h>long a=10000,b,c=2800,d,e,f[2801],g;main(){ for(;b-c;) f[b++]=a/5; for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a) for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b); scanf("%s"); return
蒙特卡罗算法计算圆周率PI(C++)
蒙特卡罗(Monte Carlo)算法计算圆周率的主要思想:给定边长为R的正方形,画其内切圆,然后在正方形内随机打点,设点落在圆内的概为P,则根据概率学原理: P = 圆面积 / 正方形面积 = PI * R * R / 2R * 2R = PI / 4。 即 PI=4P。这样,当随机打点足够多时,统计出来的概率就非常接近于PI的四分之一了。 #include <iostream>#inclu
利用spark进行圆周率的计算
package exampleimport org.apache.spark.{SparkContext, SparkConf}import scala.math.random/*** 利用spark进行圆周率的计算* Created by 汪本成 on 2016/6/10.*/object SparkPai {def main(args: Array[String]) {val con
简单计算圆周率任意位数Python代码
先上代码: import mpmath # 设置计算精度(小数点后的位数) precision_bits = 10000000# 使用mpmath库计算圆周率近似值 mpmath.mp.dps = precision_bits / 10.0 # 设置精度 pi_value = mpmath.pi # 计算圆周率 # 输出结果
简单计算圆周率任意位数Python代码
先上代码: import mpmath # 设置计算精度(小数点后的位数) precision_bits = 10000000# 使用mpmath库计算圆周率近似值 mpmath.mp.dps = precision_bits / 10.0 # 设置精度 pi_value = mpmath.pi # 计算圆周率 # 输出结果
python基础编程小实例5——计算圆周率
编程语言:python3.9 题目 求解圆周率可以采用蒙特卡罗方法,在一个正方形中撒点,根据在1/4圆内点的数量占总撒点数的比例计算圆周率值. 请以123作为随机数种子,获得用户输入的撒点数量,编写程序输出圆周率的值,保留小数点后6位。 from random import random, seedwhile True:s = input('输入投掷的点数(输入#结束程序):')if
Python圆周率问题
来源:Python语言程序设计 -嵩天 一、问题描述 计算圆周率pi的值。 二、解决思路 如下图所示,向含有半径为1的1/4圆的11的正方形中撒1000010000个点,计算落入圆中的点数与正方形内的点数的比值。比值即为1/4圆的面积,也为1/4pi的值。 三、代码 '''如笔记中所示图:向含有半径为1的1/4圆的1*1的正方形中撒1000*1000个点,计算落入圆中的点数与正方
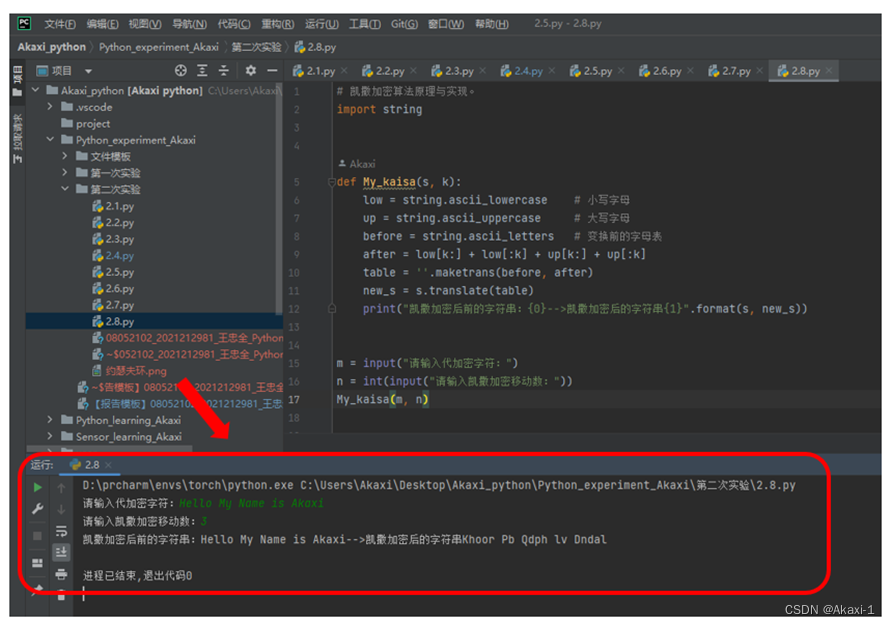
【Python实验设计】BMI计算 / 整数除法 / 蒙特卡洛近似圆周率 / 枚举法验证6174猜想 / 约瑟夫环 / 转盘抽奖 / 能力值 / 凯撒加密
目录 一、【计算BMI指数】 二、【输入整数相除】 三、【蒙特·卡罗方法计算圆周率近似值】 四、【使用枚举法验证6174猜想】 五、【模拟报数游戏(约瑟夫环问题)】 六、【模拟轮盘抽奖游戏】 七、【能力值累计】 八、【凯撒加密算法原理与实现】 一、【计算BMI指数】 输入:身高tall与体重kilo 输出:身体的BMI指数和BMI等级“过轻、正常、过重、肥胖、严重肥胖
编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...
Python计算的位数 在电脑上做了一个实验,看看python能计算到多少位,一下是结果。 x = math.sqrt((3)) print ("%.53f"%(x)) print ("%.63f"%(x)) print ("%.83f"%(x)) 1.73205080756887719317660412343684583902359008789062500 1.7320508075688771
今天是圆周率节,我们一起来用C++来求π吧!
前言 3.1415926535897932384626433832795… 不好意思,小编我只能被到这里了,当然我觉得做题只要3.14就够了,没必要背那么长的啊。。。当时我上小学时总是和同学们比背π,后来发现也没什么必要哈~当时我们班有能背到100位的,还被我们膜拜了一番(虽然背到30几位我们也不知道他是不是在乱说)。当然了,如果哪位想锻炼以下记忆力的,你尽管背好了。(Haha)因为圆周率
4.5 Python 实例6-圆周率的计算
本文内容为北京理工大学Python慕课课程的课程讲义, 将其整理为OneNote笔记同时添加了本人上课时的课堂笔记, 且主页中的思维导图就是根据课件内容整理而来, 为了方便大家和自己查看,特将此上传到CSDN博文中, 源文件已经上传到我的资源中,有需要的可以去看看, 我主页中的思维导图中内容大多从我的笔记中整理而来,相应技巧可在笔记中查找原题, 有兴趣的可以去 我的主页 了解更多计算机学科的精



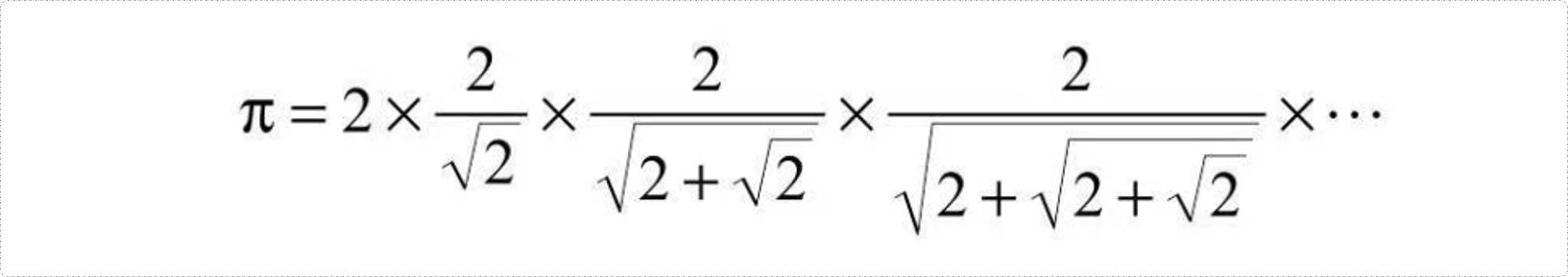
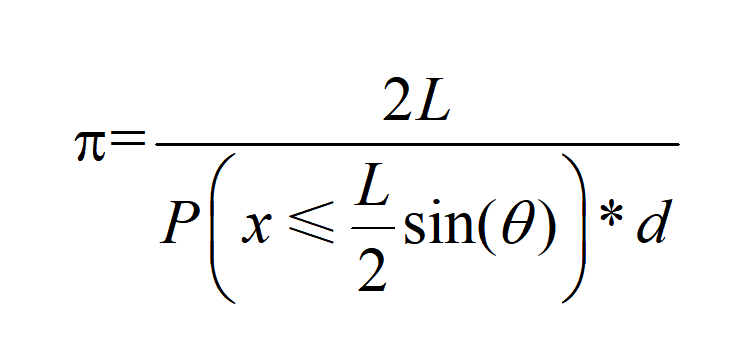







![编写python程序计算下面各表达式的值 根号派2+3,[宜配屋]听图阁 - Python计算开方、立方、圆周率,精确到小数点后任意位的方法...](https://img-blog.csdnimg.cn/img_convert/783bc90990f846659eddfcbd0692f8ee.png)

