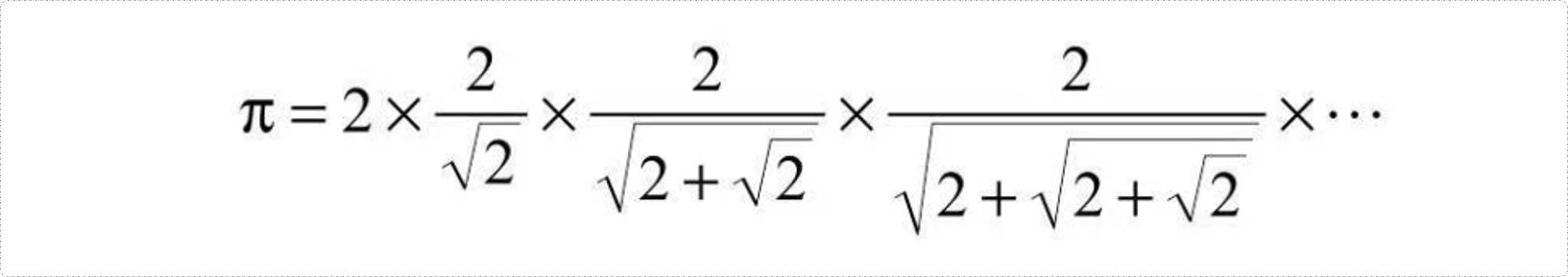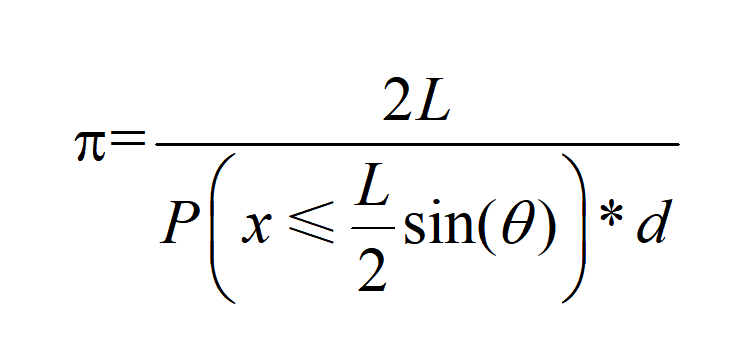用割圆术求圆周率π

本文主要是介绍用割圆术求圆周率π，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

圆周率π的递推公式如下：

     

     以半径为1的圆开始，依次在圆内画正六边形、正十二边形、正6n边形...。

     只有n趋近于无穷大，便可以得到足够接近圆的正多边形，计算的圆周率π也就越精确。

完整代码如下：

package cn.whut.num;
import java.util.Scanner;
public class pai {
static void cyclotomic(int n)			//割圆术算法
{
int i,s;
double k,len;
i=0;
k=3.0;					//初值
len=1.0;					//边长初值
s=6;						//初始内接正6边形
while(i<=n)
{
System.out.printf("第%2d次切割,为正%5d边形,PI=%.24f\n",i,s,k*Math.sqrt(len));
s*=2;					//边数加倍 
len=2-Math.sqrt(4-len); 		//内接多边形的边长 
i++;
k*=2.0;        
} 
}
public static void main(String[] args) {
int n;
System.out.print("输入切割次数:");
Scanner input=new Scanner(System.in);
n=input.nextInt(); 			//输入切割次数
cyclotomic(n);				//计算每次切割的圆周率
}
}

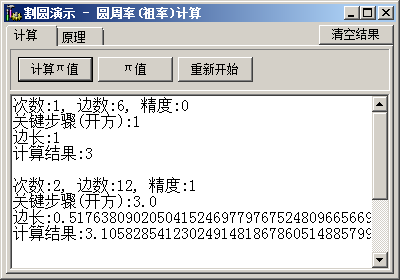
效果如下：

 

 

 

这篇关于用割圆术求圆周率π的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---