命题逻辑专题

数理逻辑学习笔记[1] 命题逻辑的形式系统

文章目录 2 命题逻辑：语法2.1 形式系统形式系统形式证明演绎定理形式系统的性质一致、平凡、单调极大一致勘误集ml-2_1.pdf 2 命题逻辑：语法 2.1 形式系统形式系统 Q: 如何理解“形式（演绎）系统中有关符号的一切行为和性质不依赖符号特定的意义和具体的性质”？用常微分方程的形式幂级数解举例阐述。 A: 提示：形式上规定针对幂级数可以逐项求微分或积分，而

数理逻辑学习笔记[0] 命题逻辑：语义

文章目录 1 命题逻辑：语义1.1 命题和连接符1.2 真值函数和真值表1.3 操作和替换规则1.4 范式1.5 连接符的完备集1.6 推理及有效性勘误集ml-1_1.pdf 1 命题逻辑：语义 1.1 命题和连接符 Q: 数学语言，如“ x 0 x_0 x0是集合 X X X的最大元”是符号语言嘛？如何把它转化为符号语言？ A: 不是。数学语言是自然语言+记号。 x 0

离散数学命题逻辑连接词的解释

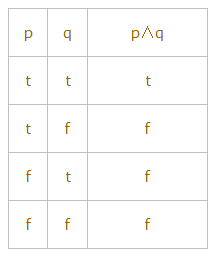
命题逻辑连接词在自然语言中，常常使用“或”，“与”，“但是”等一些联结词，对于这种联结词的使用，一般没有很严格的定义，因此有时显得不很确切。在数理逻辑中，复合命题是由原子命题与逻辑联结词组合而成，联结词是复合命题中的重要组成部分，为了便于书写和进行推演，必须对联结词作出明确规定并符号化。下面介绍各个联结词。 (1)否定定义1-2.1设p为一命题，p的否定是一个新的命题，记作┓p.若p为t, ┓

离散数学例题——1.数理逻辑（命题逻辑）

有ABC三个猜测甲乙丙三个球队中的冠军，三个人的猜测如下: A:冠军不是甲，也不是乙 B:冠军不是甲，而是丙 C:冠军不是丙，而是甲已知其中有一个人说的完全正确，一个人说的都不对，而另外一个人恰有一半说对了，据此推算，冠军应该是 A.甲 B.乙 C.丙 D.不确定因此，只有PQR=100时符合要求。证明公式等价基本等价公式判断((P→Q)^(Q→R))→(P→R)的类型

命题逻辑｜析取、合取和蕴含到底什么意思

如是我闻：在逻辑学中，“析取”、“合取”和“蕴含”这些术语的中文翻译是有其逻辑和哲学基础的，它们准确地反映了这些逻辑操作的本质。虽然他们被翻译的很高级，但并不能让人一下子就明白。析取 (Disjunction) 原理：析取对应于逻辑中的“或”操作，表示在两个命题中至少有一个是真的。逻辑表达式为 p ∨ q p \lor q p∨q，读作“ p p p 或 q q q”。理解： “析取”

《离散数学》第三章：命题逻辑（第一部分）

3.1什么是命题 3.1.1命题和非命题注意：数理逻辑研究的中心问题是推理，而推理的前提和结论都是命题。因而命题是推理的基本单位。定义：具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”，称为真值。真值只有 “真”和“假”两种，分别用“T”(或“1”) 和“F”(或“0”)表示。注意：一切没有判断内容的句子，如命令句 (或祈使句)、感叹句、疑问

Knowledge 4命题逻辑形式推演（horn clauses和definite clauses（受限制子句））

目录 1.写在前面 2.horn和definite clause的理解 3.Modus Ponens肯定式推理 4.forward chaining前向推理过程 4.1 forward chaining前向推理可靠性和完备性证明 5. Backward Chaining后向推理 6.前向推理 VS 后向推理 7.总结家庭作业 1.写在前面我们讲过了命题逻辑中形式推演的

离散数学习题1.1 命题逻辑

图源：文心一言离散数学习题记录，仅节选习题~🥝🥝 面对每个小节动辄30+道题的庞大题量，我深知，以我计穷智短的天资与精卫填海的刷题速度，即便日以继夜地奋战，累成被山西老陈醋泡过的腊八蒜，时间仍显得捉襟见肘~因此，每个类型的题目我随机仅挑选1-2道解答~🥝🥝 作为初学者的我，这些习题主要用于自我巩固。由于是自学，答案难免有误，非常欢迎各位小伙伴指正与讨论！👏💡 第1版：

$第二部分命题逻辑等值演算$