本文主要是介绍Knowledge 4命题逻辑形式推演(horn clauses和definite clauses(受限制子句)),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.写在前面
2.horn和definite clause的理解
3.Modus Ponens肯定式推理
4.forward chaining前向推理过程
4.1 forward chaining前向推理可靠性和完备性证明
5. Backward Chaining后向推理
6.前向推理 VS 后向推理
7.总结
家庭作业
1.写在前面
我们讲过了命题逻辑中形式推演的两个系统,一个系统由11条规则构成,另外一个系统只有一个规则,这次我们讲一个和归结原理差不多的霍尔子句和受限制的子句。归结原理实际上是一个搜索的问题,时间复杂度非常高,我们现在引入一个新的概念霍尔子句,是命题逻辑中一个子集,也就是说,对这个KB中每一个具体的sentence他的形式有一个限制。在这些sentence有限制的情况下,我们可以用一套新的规则来推演。在这种有限制的情况下,我们的形式推演系统会变得更加的高效。
2.horn和definite clause的理解
我们上一个博客介绍了resolution规则,证明了resolution归结是既sound也是complete的,但是这个限定在命题逻辑中。这个特性当然很好,可是在很多的case里面,它的效率不够好,基本上两两都去check,大致上pronominal的时间,可是我们还是希望有更好的效率。如果我们今天把propositional logic这个范围再缩小一点的话,缩小到什么地步呢,我们缩小到两种,我们叫两种case,一个叫definite clause,definite clause是在一个clause里面,只有一个是正的,只有一个literal是positive,那另外一个是比较general一点点的horn clause,horn clause是 at most一个是positive,也就是说里面可以全部是negative,至多有一个正的。
其实我们也可以看一下horn clause的一些特性,horn clause基本在resolution底下它是closed,意思就是说,你把两个horn clause做resolution,每一个horn clause里面最多只有一个是正的,那你在做resolution里面会把一个正的跟一个负的拿掉,所以,这两个clause里面合起来最多两个正的,那你因为在做resolution的过程中,又会把一个拿掉,所以你最后这个结果一定也是at most one positive,所以resolution结果还是一个horn clause。definite clause也是一样,definite clause只有一个正的,也是一个和一个,那你就是刚好两个,那这个resolution会把一个正的和一个负的拿掉,所以你会刚刚好得到一个只有一个正的,也就是两个definite clause resolution结果同样是一个definite clause。
我们在讲horn clause和definite clause时候,有另外一种讲法,我们会把它定义一个正的,或是最多一个正的,它的重点就是,其实它就是implication,也就是一堆东西只有一个正的,比如说 ¬A V ¬B V ¬C V D 这个样子,就是一个definite clause(只有一个正的),可以把它拆成 ¬(A ^ B ^ C)V D ,就是 A ^ B ^ C =>D (=>是implies),这个是horn clause的另外一种看法。全部都是true的话,就可以imply一个symbol。如果有一些symbol的合取,然后imply一个symbol。
我们默认用大写字母表示的都是正文字,加上否之后为负文字受限制子句definite clauses(还是很多项的析取):我们这些文字中,有且仅有一个是正文字,其他的都是负的(=1)霍尔子句horn clauses:最多只有一个为正的子句,正文字。(小于等于1)3.Modus Ponens肯定式推理
我们给出一个KB ,我们要根据这个KB推出一个a,只不过在这个时候,我们的KB中每一个sentence都是霍尔子句,a也是霍尔子句,KB是这些霍尔子句的集合。这个时候,我们也有一个规则是Modus Ponens(肯定式推理)。
和归结原理差不多,中间一个横线,上面是前腱,前腱中每一个sentence都是一个霍尔子句,一共有N+1个霍尔子句。右侧是b,我们可以推出来下面的b。

4.forward chaining前向推理过程
如果我们关注horn clause 和definite clause中的话,我们可以用所谓的forward和backward chaining来做,其实forward chaining其实很单纯,就是所谓的modus ponens(Modus Ponens肯定式推理),因为我们刚刚讲的horn clause和definite clause就是下面这个东西

接下来还有很多前面已知的东西,如果我前面每一个都已知,有不同的clause a1,a2等,clause之间是and连接起来的,所以全部都知道,也就是说如果我知道alpha 1一直到alpha n我都已知,这个chain里我全部都知道,那modus ponens做的事情就是你得到这个结论 β 。就是知道已知前提的情况下,得到的结论。这是modus ponens上的。如果你直接如果用resolution apply在horn clause的话,你得到其实就全等于modus ponens。这个你可以有兴趣的同学可以看一下,这个其实也是一种resolution,可以把它写成下面红色字体这种:
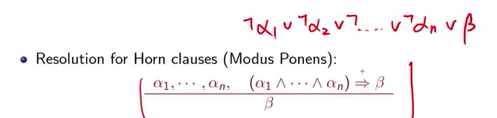
这个horn clause 写成了上面红色的那个CNF合取范式的形式,用resolution的话,就是这两个消掉,对不对,然后你再apply一次,这两个再消掉,好,一直apply到第n次,这个消掉,好,你就会得到这一个 β 。
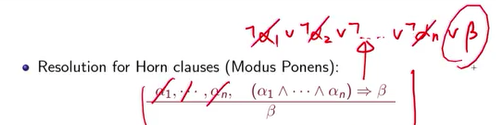
这一样是resolution,这两个是全等的。我们用forward chaining概念就是这样。你要得到这个结论,然后你只要去记录一下已知前提数量,这个例子里面其实也有数量,就是n个,之后就开始降低这个数量,就是如果已知任何事情就开始降低,降低到0的时候,你就得到这个结论β,当然你如果有点效率,就会可能要reduce,要小心重复的出现,就是如果P imply Q ,Q imply P ,小心不要一直重复这件事,这边有个伪代码,code看一看就好,我们只用例子讲解,其实还蛮单纯的,它其实就是用count来decrease。

我们来看看forward chaining怎么做,这是一个例子
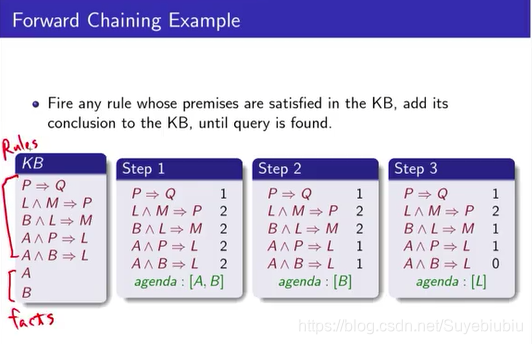
就是我的KB是左侧这个样,因为它都只定义在horn clause上,最多只有一个可以是正的,A B就是都没有负的literal,那只有A B这两个是正的,那像第二句L^M =>P 只有P是正的(可以将这句改写成CNF:¬ L V ¬M V P)。习惯上把下面两个叫做facts,上面叫做rules。因为这个A,其实就是true imply A,我们刚刚有讲,这两个是equivalent的。
那接下来forward chaining做的事情就是把已知的fact加入agenda里面,然后,把所有的刚刚的rule里面的未知的数量count一下(后面的12222这种),接下来agenda中的东西一个一个拿出来,你先把A拿出来,就是A是已知,之后所有它的前提里面有A的,全部都把它减1,只有两个有A,前面有A,所以你就把它2减成减1减1,就变这样step2这样。然后之后你再把agenda里面剩下B,pop B出来,所有前面有B的你再相减,得到step3。通过减法得到0说明我的未知已经全部知道了,所以我可以得到结论L,所有0的那个结论push进你的Q agenda里面,所以在这个时间点,你会把L放在你的agenda,之后继续做。

然后,因为你L已知,你就会再减1,然后你就会把它减成1和0,那一旦减成0以后,你就这个M你也得到了,你就把M再 push进agenda里面,然后之后再pop,把M pop出来,你就会把这一个有M的再减1,所以这个得到0,0的话你就代表你就得到P,P再push进agenda,之后你会得到第一个就终于可以减了,这个1可以减成0,然后之后你得到Q,Q的时候看你实际上怎么做了,那你可能还会再次得到L这个东西,那你可能会再把L push进agenda,那这里面看你要不要去做一些check,你如果有做一些check的话,你知道L刚刚已经知道了,那就不需要再度知道。那这样就这样一直做下去,那做到最后,直到你想要的东西有被有被infer推理出来,在agenda里面都是已知的事实,像我们刚才就已知A、B,然后我们已知A、B、L、M、P、Q为True。这两个原本是A、B知道的,那剩下这四个是forward chaining做infer出来的东西。就这样一直直到你的query找不到,或者你已经全部找完还没有就可以结束。我们每一个implication,有多少个原子命题,我们就扫多少轮。
4.1 forward chaining前向推理可靠性和完备性证明
可靠性:跟上次那个归结原理的时候一样,可以使用真值表的方法证明
完备性证明:
跟resolution很像,我们把它假设FC已经达到了faced point,你叫closure也行。一个faced point就是找不出新的东西。也没有新的inference可以出来。在这个时间点呢,我们来做一个model,我们给你一个初始assignment。已知的,进过agenda的symbol。你全部都把它设为True,assign成True,所有未知的你全部把它设成false,这是一种model。也就是说我们没有看到的,我没证出来就当做你是错的,然后我们来看这个model怎么样,我们接下来claim宣称这个model会使得KB里面的每个clause都为真,这个就是completeness了。我们证明这件事就可以了。证明model可以让KB里面每个式子都为真,意思就是你只要是对的,那我一定能拿到。
很简单,一样用反证法来证明。我们刚才讲每个clause都为真,我们可以先假设我这个claim是错的,就是KB里面有一个clause为false。假设是下图中圈出来的clause为false:

这个clause为false的话,那是怎么样子呢?就是你必然是false的话,因为A implys B,B就是false的话,必须是前提是true,结论是false,这整句话才是false(implication真假为假 ,其余为真 )。也就是说圈出来的部分前面这个都是true,后面是false,整个才会为false。但是这个在code中是不可能存在的,因为前面的是true,counter会被redue到零。这个clause原本是K,counter就是k,你知道一个a1为true,k就减一,你知道a2为true,k再减一,你前面全都为true了,k就会减到0,降到0之后,你会把β放进agenda中,按照我们的assignment,β会被设置为true,不会设置为false。表示我们的假设FC其实还没有达到fixed point,有新的东西还可以infer出来,β是新的结论。违反我们一开始的假设:我们说FC已经达到fixed point情况下,我们给一组assignment,这组assignment一定可以使得KB中每一个clause为真,就证明了forward chaining是complete的。只要你KB可以entail的东西 ,我forward chaining一定可以infer出来(只要你蕴含的知识,我都可以形式推演出来)。
接着看,如果KB entailment q,我们知道M(kb) 含于 M(q)中,也就是M(q)的范围更大一些,如果我们假设了一个model使得KB为true,那么这个model一定会使得q为true。只要KB entailment q,无论q是什么,我的FC 一定已经infer过了。这个就是complete的证明,只要你是KB entailment的 q,我FC 都可以找到q是正确的这个结论。


5. Backward Chaining后向推理
我们的前向推理是从fact开始,通过count和减一运算得到新的fact,直到找到我们的目标。我们同样可以反向操作,从目标反过来看,看能不能找到这个目标。一样可以类似来写,但是我们现在换个说法,用一个and-or-graph。比如 A ^ B => C ,我们想要得到C,必须要同时知道A和B,我们可以画一个圆弧表示。
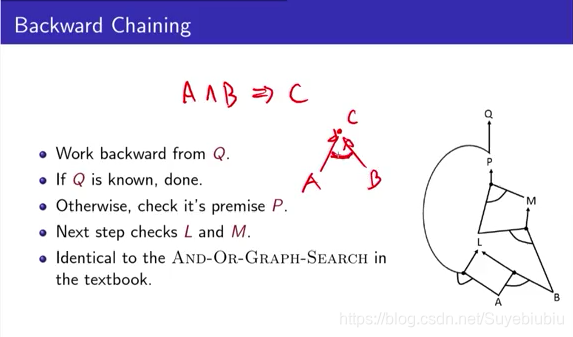
我们来看一下怎么操作:
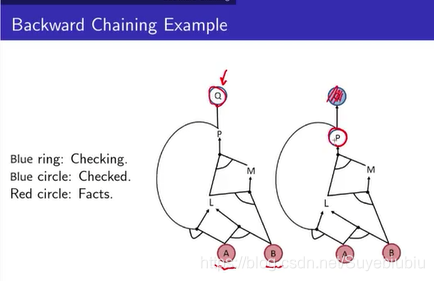
举一个例子,用红色的圆圈当做已经知道的fact,像我们刚才KB中,我们知道A,B为true,然后实心的当做已经check过的,我们会从Q开始,Q就是我们现在正在看的东西,Q看过了就会把Q涂实,然后接下来看P,因为我们要得到Q为真的话,我们的前提是P为真。接下来,P要为真的话,就要看L和M,L和M中间是and,必须要求L和M都要为真,接着先看L要是为真的话,A一定要为真,而且P为真,这个时候遇到了circle,代表我们走不通,只好试着走另外一条右路,AB为真是已经知道的fact,所有得到L为真。
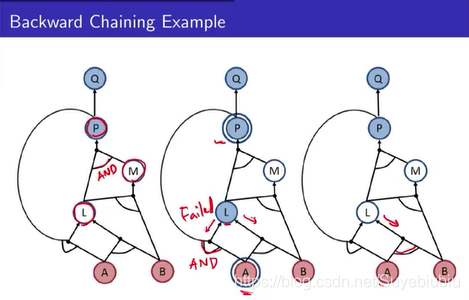
这个时候就把L为真加入到你的fact当中去(红色圆圈),接下来,有一个正在check的的M,我们之前要LM同时为真,再看一下M,M只有一条路,需要LB为真,这个已经是在fact中已知的了,所以就会得到M是为真,放到fact中,继续得到P为真,Q为真。这个过程就是backward chaining 的方式。从后面用tree search的方式来search。
6.前向推理 VS 后向推理
FC和BC的时间复杂度基本上都是跟你的KB的大小有关系,但是有一些特性不同,我们把FC称为data-driving。就是你有哪些资料,一开始你就一直展下去,BC就是goal-driven,你需要一个目标,从目标开始导,一般而言,BC比较像是人类在做的事情,先有目标再去找方法,FC不太像人类,但是FC有好有坏,好处是可以把所有KB 能entail的东西全部导出来。可以在这个过程中,缺点是可能导出来了很多无用的conclusion,可能跟你的目标毫无关系。
一般而言,BC是从目标出发,速度上可能比FC更快一些。
前向:从条件出发推结论
后向:从结论出发,一般更加高效,因为前项有可能会推出来一些冗余信息,和结论并没有什么关系。
7.总结
我们前段时间都是在讲Propositional logic命题逻辑,我们总结一下命题逻辑的优缺点,当然好处还是很多的,第一个是像它是declarative的,你只要把它宣告出来,那后面的influence可以蛮系统化了。很多一些特性包含像它是compositional,它是可以组成的,就是它的语意基本上譬如说,B1,1 ^ P1,2 ,其实语意上不用额外定义,只要我已知的semantics,我就可以定义它的semantics。

还有它的意义,我们称为context independent与上下文无关。当然了命题逻辑中也会有很多的缺点,它的expressive power表达能力是不够的,
这个时候,我们命题逻辑就讲完了,三套推演规则:一个有11条规则组成。一个是只有一个归结原理。还有一个是KB中句子有了限制。限制为都是霍尔子句,有一个mp规则。每一套归结都是sound也是comple的,所以说命题逻辑是一种declarative声明式的。这种东西首先是可以通过合取析取等方式连接起来。而且我们这种命题逻辑是context-independent(跟上下文无关),所以命题逻辑表达能力有限的
命题逻辑表达能力有限的:比如wupoos中,在深渊旁边有微风,我们在用命题逻辑写这条规则的时候,每一个格子分开写。接下来我们定义一个一阶谓词逻辑,在一阶谓词逻辑中一条规则就可以表述这个东西。
显然在一阶谓词逻辑要重定义我们的language,我们要引入更多的符号,在新的语言下面,我们可以定义形式推演规则,同样在一阶谓词逻辑也有归结原理,也有霍尔子句和mp规则。
家庭作业

这篇关于Knowledge 4命题逻辑形式推演(horn clauses和definite clauses(受限制子句))的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!