公理专题
概率的三条基本公理 | 布尔不等式的应用(举例)
概率论的三条基本公理由俄罗斯数学家柯尔莫哥洛夫(Andrey Kolmogorov)在1933年提出,被称为柯尔莫哥洛夫公理。它们构成了现代概率论的基础。这三条公理如下: 公理 1:非负性 公理 2:规范性 公理 3:可加性 布尔不等式 对于任意的事件集合 { A 1 , A 2 , … , A n } \{A_1, A_2, \ldots, A_n\} {A1,A2,…,An}
再论任何图≌自己这一几何最最起码常识推翻平面公理
黄小宁 有了解析几何使人类对直线和射线的认识有革命性的飞跃。几何学有史2300年来一直认定起点和射出的方向都相同的射线必重合,任两异射线必有全等关系;解析几何使我发现这是2300年肉眼直观错觉。 h定理(参考文献中的定理):数(点)集A=B≌B的必要条件是A≌B(初等几何应有最最起码常识:元点不少于两个的图B≌B)。 如图所示射线A:x ≥ 0不保距地伸缩变换为射线B:u=x^n(n=2,3
任何图≌自己这一几何最最起码常识推翻直线公理和平面公理
黄小宁 与x∈R相异(等)的实数均可表为y=x+δ(增量δ可=0也可≠0)。因各实数的绝对值都可是表示长度的数故各实数都可是一维空间“管道”g内点的坐标。于是x∈R变换为实数y=x+δ的几何意义可是:“管道”g内R轴上的质点x∈R(x是点的坐标)运动到新的位置x+δ=y还在管道g内即实数的改变可几何化为g内质点的位置的改变。R可几何化为R轴, R各数x可几何化为R轴各点,两变数可几何化为g内两动点
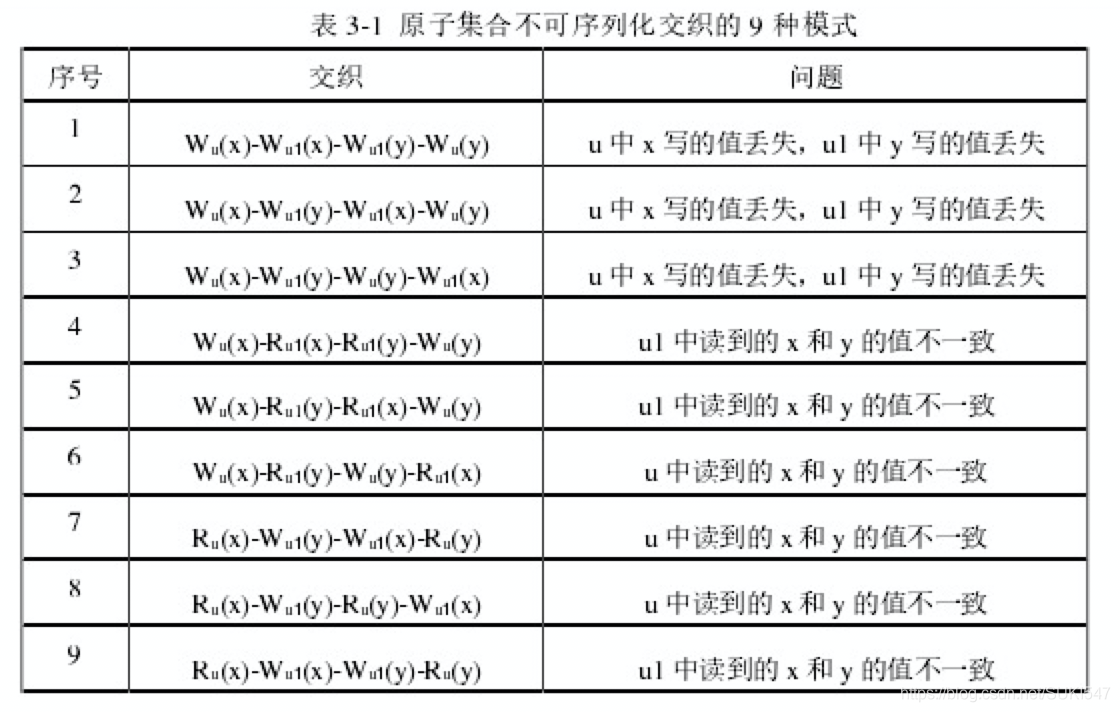
【并发理论】事件、执行轨迹、可行性公理、最大因果模型
文章目录 事件执行轨迹可行性公理 (Feasibility Axioms)最大因果模型(Maximal Causal Model) 原内容来自 基于约束求解的并发程序错误预测方法研究 — 背景 — 任意线程都能通过执行一组原子操作来访问并发对象;若对某些并发对象进行访问的原子操作序列能由并发程序的执行产生,则表明这些原子操作序列满足了规定的顺序要求。这些顺序要求被称为
第2章-从头开始:自然数 2.1-Peano 公理
一些定义 数零~0增长运算,n++代表 n 的后继1是数0++,2是数(0++)++,3是数((0++)++)++,…1 = 0++,2 = 1++,3 = 2++,…自然数集 N \mathbb N由 0 和每个可由 0 经增长而得到的所组成的 公理内容 图片中分别为公理2.1~2.5公理2.3是为了避免“回归事件(循环)”公理2.4解决了增长发生回归但不回归到0的异常情况 公理2.
【函数依赖,完全函数依赖与传递函数依赖,函数依赖相关的几个概念,关于函数依赖的公理和定理,函数依赖集的最小覆盖,关系的第1范式和第2范式,关系的第三范式和Boyce-Codd范式】
文章目录 一、函数依赖1.函数依赖的定义2.函数依赖的示例3.函数依赖的特性4.函数依赖的提取练习 二、完全函数依赖与传递函数依赖1.部分函数依赖与完全函数依赖的定义2.传递函数依赖的定义 三、函数依赖相关的几个概念1.候选键的定义2.外来键的定义3.逻辑蕴含的定义4.闭包 四、关于函数依赖的公理和定理1.函数依赖的Armstrong公理2.关于函数依赖的推论一一定理3.属性闭包 五、函数依