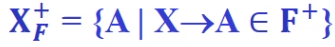本文主要是介绍数据依赖的公理系统,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数据依赖的公理系统
在说公理系统前,要理解函数依赖的概念(可以看我博客里面讲范式的文章也有提到函数依赖的定义)
一 函数依赖
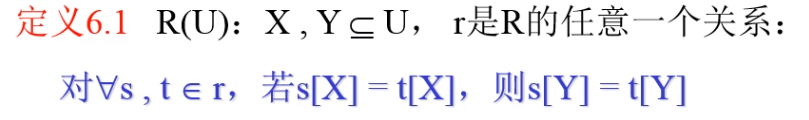
理解是,我们在R里面任意找一个r关系,对于这个关系的元组s和t,当s和t在属性(组)X上面相等,则s和t在Y属性(组)上也相等。这样被称为,X函数确定Y函数或者说Y函数依赖于X函数(X->Y).
二 逻辑蕴含

理解是,在R关系模式里面,U是属性集,F是函数依赖集(一些函数依赖组成),在这个关系模式里面,如果所有关系都满足 X->Y这一个函数依赖,则成为F逻辑蕴含X->Y。
例如
R<U,F>: U = {A,B,C} F={A->B,B->C}
则有,F逻辑蕴含A->B,AB->B,A->C
理由是:A->B是在F函数依赖集里面显式给出的,AB->B B属性式AB的一个子集,所以AB必然决定B, A->C则是通过函数依赖传递得到的。
Armstrong(阿姆斯特朗)公理系统
它是一套推理规则,是模式分解算法的理论基础,
以下是公理系统的重要规律和推论
规律
- 自反律(Reflexivity):若Y X U,则X →Y为F所蕴含。
//X包含Y,即Y是X的子集,所以必然有X决定Y - 增广律(Augmentation):若X→Y为F所蕴含,且Z U,则XZ→YZ为F所蕴含。
//可以在函数依赖两边加一样的属性。 - 传递律(Transitivity):若X→Y及Y→Z为F所蕴含,则X→Z为F所蕴含。
导出推论:
- 合并规则:由X→Y,X→Z,有X→YZ
- 伪传递规则:由X→Y,WY→Z,有XW→Z。
- 分解规则:由X→Y及 Z含于Y,有X→Z。
性质
有效性/确定性:函数依赖集F根据公理推出的每一条函数依赖都是正确的,而且都在F的闭包中。
完备性:函数依赖集F闭包中所有的函数依赖都可以用公理导出。
三 函数依赖的闭包
定义:若F为关系模式R(U)的函数依赖集,我们把F以及所有被F逻辑蕴涵的函数依赖的集合称为F的闭包,记为F+。
函数依赖的闭包指F所逻辑蕴含的所有成立的函数依赖,而对于平凡函数依赖(如 (A,B)—>A )都被F所逻辑蕴含,即便F是一个空集,其闭包也包含很多函数依赖
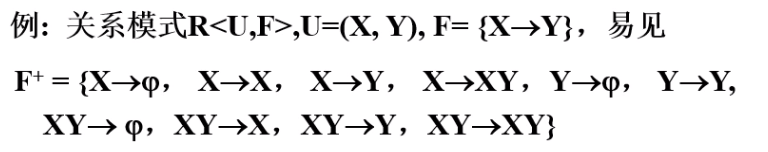
这样把闭包的所有成员全部罗列出来通常是没有很大意义的。
属性集的闭包
定义:设F位属性集U上的一组函数依赖,X含于U,则
称为是属性集X关于函数依赖集F的闭包
在F确定的情形下,也可以写成X+
*例如
R<U,F>: U ={A,B,C} F={A->B,B->C}
则X关于函数依赖集F的闭包是ABC({A,B,C}的简写)
因为A->A,A->B,A->C都可以直接或者间接得出
前面提及是罗列出闭包的所有成员是不实际的,有很多,而且是意义不大的一件事情。但是我们如果真的要表示一个闭包时该怎么办呢?或者说我们在要判断一个函数依赖是否成立(是否在一个函数依赖集里面)时,我们要怎么求解呢?
接下来的定理,它将函数依赖是否成立 转化为 属性集闭包的问题

说明:X决定Y当且仅当Y时X属性集闭包的一个子集 或者可以说, Y要在X属性集闭包里面,才可以说X确定Y.
这样我们就把本来要计算一个函数依赖闭包的问题,转化位了一个属性集闭包的问题。
对于属性集闭包的求解
我们提供一套算法:

例题:
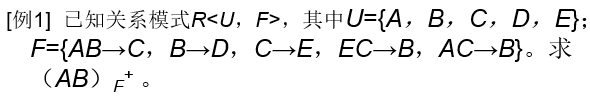
解


这篇关于数据依赖的公理系统的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!