【并发理论】事件、执行轨迹、可行性公理、最大因果模型

本文主要是介绍【并发理论】事件、执行轨迹、可行性公理、最大因果模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原内容来自 基于约束求解的并发程序错误预测方法研究
— 背景 —
任意线程都能通过执行一组原子操作来访问并发对象；若对某些并发对象进行访问的原子操作序列能由并发程序的执行产生，则表明这些原子操作序列满足了规定的顺序要求。这些顺序要求被称为并发对象的 序列化规范（serial specification）

序列化规范是顺序要求，是并发程序对并发对象访问产生的原子操作序列顺序。

并发对象多为两种：

1. 共享内存地址：对共享内存地址有read和write操作，序列化规范定义了每一个read值＝最近前一个write的值
2. 不可重入锁：对每一个不可重入锁有acquire获得锁、release释放锁操作，序列化规范定义了acquire和release 数量差为0或1，且所有连续的获得锁、释放锁操作是对同一个线程进行的操作。

---

事件

事件(Event)是线程在并发对象上执行的原子操作，表示为“属性-值”元组
属性有：访问当前并发对象的线程thread、 对该并发对象进行的操作类型op、该事件访问的并发对象target、对并发对象进行的操作值data 如(thread=t1,op=read,target=o,data=1）意为线程1对共享变量o进行读操作，读值为1，简写为read(t1,o,1)
对于两个事件e1,e2，当且仅当所有属性都相等，才称为这俩个事件相等。

执行轨迹

执行轨迹抽象为一组事件序列 $\tau =<e_1,e_2,...e_n>$

$\tau |o：执行轨迹\tau 对并发对象o的事件序列$
$\tau |t：执行轨迹\tau 中属于线程t的事件序列$
$\tau |t,o：执行轨迹\tau 中线程t访问并发对象o的事件序列$
${\tau }_e：执行轨迹\tau 中包含事件e在内的前缀事件序列，例\tau ={\tau }_{1}e{\tau }_2，则{\tau }_e={\tau }_{1}e$
$las{t}_{op}(\tau ):执行轨迹\tau 最后一个op操作的事件$

顺序一致性执行轨迹：当且仅当对每个并发对象o,事件序列τ|o 都满足序列化规范时，执行轨迹τ被称为顺序一致性执行轨迹。包含以下要求：

• 读写一致性： read读的值是执行轨迹在read之前且距离该read事件最近且和read访问同一个共享内存地址的write值。设e为该read事件 读写一致性可形式化表示为 $data(e)=data(las{t}_{write}({\tau }_e|target(e)))$
• 锁互斥：每个release事件之前都有同一个线程且同一个锁变量的acquire事件与之匹配，且对每一个acquire-release锁对 都不可与其他访问同一锁变量的锁对产生交织。$\tau |l=e_1,e_2,...e_n,若有l\le k＜n,op(e_k)=acquire则op(e_{k+1})=release，thread(e_k)=thread(e_{k+1})$
• Happens-before关系：begin事件是线程执行的第一个事件,且发生在父线程fork(t,t’)之后，e=begin(t’)为τ中事件。$\tau |t^{\prime }$是e开头的事件序列，${\tau }_e$中有且仅有fork(t,t’)必在e之前发生。
  end事件是线程执行的最后一个事件且另一线程等待当前线程终止的join事件只能发生在end之后。e=end(t’) $\tau |t^{\prime }$是以e结尾的事件序列，τ中有且仅有join(t,t’)在e之后发生

可行性公理 (Feasibility Axioms)

易知并发程序每次运行的执行轨迹均满足顺序一致性要求，但是这些顺序一致性执行轨迹之间不一定存在相关性。根据可行性公理，可由收集的顺序一致性执行轨迹推导出其他与该执行轨迹相关的顺序一致性执行轨迹，且不需要其他信息。任一并发程序P，通过P实际产生的τ构成的集合表示为 feasible（P）

可行性公理的演变过程
① feasible( P) 在交织条件下是封闭的，任意τ所满足顺序一致性的交织都属于feasible( P)(过于严格、应用弱) （满足顺序一致性情况下重新排列组合顺序） 如上图，满足顺序一致性的$\tau (1278910^{\prime }),e(10^{\prime })=read(t2,c,0)$ 就无法用公理推出
② 在①基础上，提出前缀封闭和局部确定性可行性公理，前缀 ${\tau }_e$也属于feasible§，局部情况由具体线程执行到的事件的之前事件而确定。局部确定性表示为：${\tau }_1{e}_1,{\tau }_2\in feasible(P)，{\tau }_1|thread(e_1)={\tau }_2|thread(e_1)$ 则

• ${\tau }_2{e}_1满足顺序一致性，{\tau }_2{e}_1\in feasible(P)$
• $若op(e_1)=read，且存在其他事件e_2满足e_2[data(e_1)/data]=e_1，并且{\tau }_2{e}_2满足顺序一致性，则\tau 2e2\in feasible(P)$
  e[v/data]表示用值 v 代替值data，则该等式表示e2除了其操作的变量值和e1不同外，其他属性均相同)
  考虑了交织和read操作的松弛要求 （还是不够松弛）除了read操作还有锁操作，write没有考虑。

③ 考虑分支事件的可行性公理。同意前缀封闭，认为write操作依赖同一线程在该事件之前所有read事件

• $若{\tau }_1{e}_1,{\tau }_2\in feasible(P)，thread(e_1)=t,且{\tau }_1|t\approx {\tau }_2|t(除了readwrite值，其他都相等)，则{\tau }_2{e}_1\in feasible(P)$ 前缀封闭
• $若op(e_1)=branch，(branch这里指跳转分支事件，分支事件依赖t在此分支之前所有read事件)且{\tau }_1|t,read={\tau }_2|t,read，则{\tau }_2{e}_1\in feasible(P)$分支事件
• $若op(e_1)=read，且存在其他read事件e_2满足e_2[data(e_1)/data]=e_1，并且{\tau }_2{e}_2满足顺序一致性，则{\tau }_2{e}_2\in feasible(P)$仅读值不同
• $若op(e_1)=write，且存在值v使e_1[v/data]=e_2，并且{\tau }_2{e}_2满足顺序一致性，则{\tau }_2{e}_2\in feasible(P)，若{\tau }_1|t,read={\tau }_2|t,read,则v=data(e_1)$仅写值不同
• 若 o p ( e 1 ) ∉ { b r a n c h , r e a d , w r i t e } ， τ 2 e 1 满 足 顺 序 一 致 性 ， 则 τ 2 e 1 ∈ f e a s i b l e ( P ) ， 若 op(e_1)∉ \{ branch,read,write\}， τ_2e_1满足顺序一致性，则 τ_2e_1∈feasible(P)， 若op(e1​)∈/​{branch,read,write}，τ2​e1​满足顺序一致性，则τ2​e1​∈feasible(P)，其它情况也可

此时公理较完备，可产生原子集序列化违背的执行轨迹，原子集序列化违背共有如下9种模式。能产生违背的执行轨迹则可帮助在实际程序中探测。

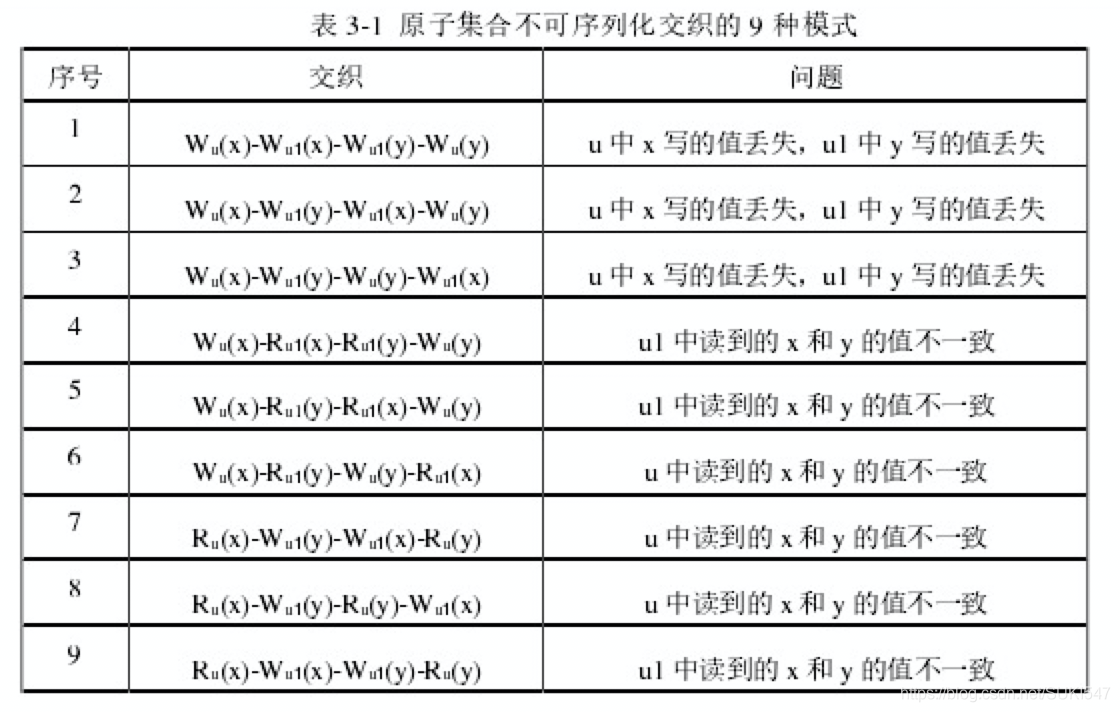
最大因果模型(Maximal Causal Model)

feasible(τ)是由能够产生执行轨迹τ的所有 程序执行产生顺序一致性轨迹构成的集合。 可行性公理为顺序一致性τ与最大因果模型feasible(τ)之间的关联提供基础。

定义 对于给定的顺序一致性执行轨迹 τ，其可行性闭包是包含其在内的执行轨迹的最小集合，记作 feasible(τ)。feasible(τ)满足前缀封闭性和局部符号确定性：

• 前缀封闭 $若{\tau }_1{\tau }_2\in feasible(\tau )，则{\tau }_1\in feasible(\tau )$
• 局部符号确定性 $假设若{\tau }_1{e}_1,{\tau }_2\in feasible(\tau )，thread(e_1)=t,且{\tau }_1|t\approx {\tau }_2|t$
  $(1)若op(e_1)=branch，且{\tau }_1|t,read={\tau }_2|t,read，则{\tau }_2{e}_1\in feasible(\tau )$
  $(2)若op(e_1)=read，且存在其他read事件e_2满足e_2[data(e_1)/data]=e_1，并且{\tau }_2{e}_2满足顺序一致性，则{\tau }_2{e}_2\in feasible(P)$
  $(3)若op(e_1)=write，$
  $1.若{\tau }_1|t,read\ne {\tau }_2|t,read,则有值sy{m}_{{\tau }_2}使得{\tau }_2{e}_1[sy{m}_{{\tau }_2}/data]\in feasible(\tau )$
  $2.若{\tau }_1|t,read={\tau }_2|t,read,则{\tau }_2{e}_1\in feasible(\tau )$
  ( 4 ) 若 o p ( e 1 ) ∉ { b r a n c h , r e a d , w r i t e } ， τ 2 e 1 满 足 顺 序 一 致 性 ， 则 τ 2 e 1 ∈ f e a s i b l e ( τ ) (4)若 op(e_1)∉\{ branch,read,write \}， τ_2e_1满足顺序一致性，则 τ2e1∈feasible(\tau) (4)若op(e1​)∈/​{branch,read,write}，τ2​e1​满足顺序一致性，则τ2e1∈feasible(τ)

总结：最大因果模型的思想有点像遗传算法的交叉和变异，除了固定的基因（顺序一致化），其他基因位置可变（交织）。也可小幅度变异（值不同）。执行轨迹会产生理论上没有语法错误但是与编程目的违背的错误（原子集序列化违背）与真实程序执行会产生的错误相同，从而减少真实实验次数集。

这篇关于【并发理论】事件、执行轨迹、可行性公理、最大因果模型的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---