余弦定理专题
一种极简的余弦定理证明方法
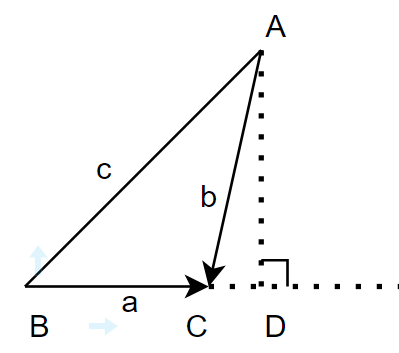
余弦定理的证明方法有很多种,这里介绍一种极简的证明方法。该方法是本人在工作中推导公式,无意中发现的。证明非常简单,下面简单做下记录。 如上图为任意三角形ABC,以点C为原点,建立直角坐标系(x轴方向任意,y轴与x轴垂直),x轴与CB夹角为 θ 1 \theta_1 θ1,x轴与CA夹角为 θ 2 \theta_2 θ2。点B的坐标为 ( a c o s θ 1 , a s i n θ
OpenCV:已知三角形的两边 求夹角的问题(余弦定理)
// 找余弦角度: 线段pt0-pt1 和线段 pt0-pt2: double angle( Point pt1, Point pt2, Point pt0 ) { double dx1 = pt1.x - pt0.x; double dy1 = pt1.y - pt0.y; double dx2 = pt2.x - pt0.x; double dy2 = pt2.y - pt0.
文本相似度算法(余弦定理)
最近由于工作项目,需要判断两个txt文本是否相似,于是开始在网上找资料研究,因为在程序中会把文本转换成String再做比较,所以最开始找到了这篇关于 距离编辑算法 Blog写的非常好,受益匪浅。 于是我决定把它用到项目中,来判断两个文本的相似度。但后来实际操作发现有一些问题:直接说就是查询一本书中的相似章节花了我7、8分钟;这是我不能接受……
python scipy使用余弦定理求句子相似度
import jiebaimport gensimimport numpy as npfrom gensim import corporafrom scipy.spatial.distance import pdisttext1 = "我去玉龙雪山并且喜欢玉龙雪山玉龙雪山"text2 = "我去玉龙雪山并且玉龙雪山玉龙雪山"text_dict = [[word for word in
HDU 3903 Trigonometric Function (三角恒等式余弦定理)
http://acm.hdu.edu.cn/showproblem.php?pid=3903 如何判断的有理性? 由这三个式子: 问题可化归为判断A,B,C的正弦和余弦是否为有理数,又由余弦定理 以及 cos(arccos x)=x 若x=p/q,则sqrt(1-x^2)=sqrt(q^2-p^2)/q 故只需判断q^2-p^2
余弦定理是怎么推导的?
余弦定理是怎么推导的? 已知余弦定理(low of cosines)表达如下: A B 2 = B C 2 + A C 2 − 2 B C ∗ A C ∗ cos θ AB^2=BC^2+AC^2-2BC*AC*\cos \theta AB2=BC2+AC2−2BC∗AC∗cosθ,其中 A B , B C , A C AB,BC,AC AB,BC,AC和 θ \theta
EM@解三角形@正弦定理@余弦定理
文章目录 abstract解三角形基本原理不唯一性 正弦定理直角三角形中的情形推广锐角三角形钝角情形 小结:正弦定理 余弦定理直角三角形中的情形非直角情形小结:余弦定理公式的角余弦形式 abstract 解直角三角形问题正弦定理和余弦定理的推导 对于非直角情形,都是直角情形的推广同过构造辅助线(垂线),来构造直角三角形,利用直角三角形的特点构建恒等方程,得到相应的定理
反三角函数、余弦定理求解角度问题——计算不收敛
在三角形关系里求解角度时,我们一般采用余弦定理、反三角函数。假设三角形的三条边分别为a,b,c,其中a,b两个边的夹角为θ(未知),则夹角θ表示为: 正常的三角形用我们已知的这种方法进行角度求解是没有任何问题的。但是,人生不会那么如意让你顺利的求得每一个想要的角度。于是会出现这样一种情况: 图源:知乎-生信洞 我们记x表示为:
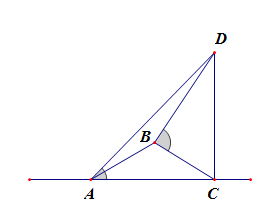
正余弦定理解三角形的实际应用
导言: 1、上节课:用正余弦定理解三角形,复习回顾 2、本节课和上节课的关系:上节课用正余弦定理解三角形,是针对三角形的数学模型来求解;而本节课需要将实际问题先图形化,转化为针对三角形的数学模型来处理的问题,如果这个环节做得好,那么到此问题就完全变成了上一节的问题。 静雅凤中$\;\cdot\;$正余弦定理的实际应用 考点:测量不可到达的高度问题,求三角形的边 要测量电视塔$AB$的高度,在$C
自己实现文本相似度算法(余弦定理)
最近由于工作项目,需要判断两个txt文本是否相似,于是开始在网上找资料研究,因为在程序中会把文本转换成String再做比较,所以最开始找到了这篇关于 距离编辑算法 Blog写的非常好,受益匪浅。 于是我决定把它用到项目中,来判断两个文本的相似度。但后来实际操作发现有一些问题:直接说就是查询一本书中的相似章节花了我7、8分钟;这是我不能接受…… 于是停下来仔细分析发现
向量空间模型(VSM)的余弦定理公式(cos)
相信很多学习向量空间模型(Vector Space Model)的人都会被其中的余弦定理公式所迷惑.. 因为一看到余弦定理,肯定会先想起初中时的那条最简单的公式cosA=a/c(邻边比斜边),见下图: 但是,初中那条公式是只适用于直角三角形的,而在非直角三角形中,余弦定理的公式是: cosA=(c2 + b2 - a2)/2bc 不过这条公式也和向量空间模型中