导言：
1、上节课：用正余弦定理解三角形，复习回顾
2、本节课和上节课的关系：上节课用正余弦定理解三角形，是针对三角形的数学模型来求解；而本节课需要将实际问题先图形化，转化为针对三角形的数学模型来处理的问题，如果这个环节做得好，那么到此问题就完全变成了上一节的问题。
静雅凤中$\;\cdot\;$正余弦定理的实际应用 考点：测量不可到达的高度问题，求三角形的边
要测量电视塔$AB$的高度，在$C$点测得塔顶$A$的仰角是$45°$，在$D$点测得塔顶$A$的仰角是$30°$，并测得水平面上的$∠BCD＝120°$，$CD＝40 m$，则电视塔的高度为__________m． 
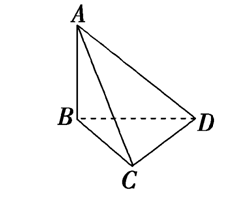
分析：设电视塔$AB$高为$x\; m$， 则在$Rt\Delta ABC$中，由$\angle ACB＝45°$得$BC＝x$. 在$Rt\Delta ADB$中，由$\angle ADB＝30°$，得$BD＝\sqrt{3}x$. 在$\Delta BDC$中，由余弦定理，得 $BD^2＝BC^2＋CD^2－2BC\cdot CD\cdot cos120°$， 即$(\sqrt{3}x)^2＝x^2＋40^2－2\cdot x\cdot 40\cdot cos120°$， 解得$x＝40$，所以电视塔高为$40 m$.
反思总结：①解三角形问题时，常常需要将立体问题平面化； ②当已知条件不在一个三角形中时，我们常常将其转化到一个三角形中，再求解即可。 静雅凤中$\;\cdot\;$正余弦定理的实际应用 考点：测量不可到达的距离问题，求三角形的边如图$A、B$两点在河的两侧，且$A、B$两点均不可到达，如果要测量$AB$的距离，测量者在河岸边选定了两点$C、D$，并测得$CD=\cfrac{\sqrt{3}}{2}km$，$\angle ACB=\alpha=45^{\circ}$，$\angle ACD=\beta=60^{\circ}$，$\angle CDB=\gamma=30^{\circ}$，$\angle ADB=\delta=30^{\circ}$，求$A、B$两点间的距离。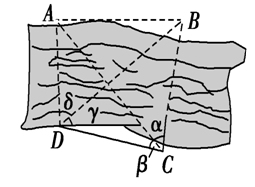 
分析：在$\Delta ACD$中，由$\angle ADC=\delta+\gamma=60^{\circ}$，$\angle ACD=60^{\circ}$，$CD=\cfrac{\sqrt{3}}{2}km$， 可得边$AC=CD=\cfrac{\sqrt{3}}{2}km$； 在$\Delta BCD$中，由$\angle BDC=30^{\circ}$，$\angle BCD=105^{\circ}$，$CD=\cfrac{\sqrt{3}}{2}km$， 故由正弦定理，可得$BC=\cfrac{DC}{sin\angle DBC}\cdot sin\angle BDC=\cfrac{\sqrt{6}}{4}$； 在$\Delta ABC$中，由$\angle ACB=45^{\circ}$，$AC=\cfrac{\sqrt{3}}{2}km$，$BC=\cfrac{\sqrt{6}}{4}$， 由余弦定理可得，$AB^2＝BC^2＋AC^2－2BC\cdot AC\cdot cos45°$， 解得$AB=\cfrac{\sqrt{6}}{4}km$
反思总结：1、怎么分析？由果溯因，题目要求解$AB$的长度，需要将其放置到一个三角形中， 图中能包纳$AB$在内的三角形有三个，分别是$\Delta ABC$和$\Delta ABD$和$\Delta AOB$， 首先能排除的是不选$\Delta AOB$，原因是已知条件都用不上。 接下来，选择的这两个三角形，从已知数据的角度看是对称的，所以随便选一个，比如$\Delta ABC$。 在此三角形中，$\angle ACB=45^{\circ}$能用上，自然还得知道边$AC$和$BC$， 要求解边$AC$，也得选个三角形，比如选$\Delta ACD$，用正弦定理求解$AC$即可； 要求解边$BC$，也得选个三角形，比如选$\Delta BCD$，用余弦定理求解$BC$即可； 到此，回到$\Delta ABC$中，用余弦定理就可以搞定问题了。 2、当已知条件转化到一个三角形中时，问题就变得迎刃而解了。 静雅凤中$\;\cdot\;$正余弦定理的实际应用 题源：2017淄博模拟；考点：测量角度问题，求三角形的角如图，在海岸$A$处，发现北偏东$45^{\circ}$方向距离$A$处$(\sqrt{3}-1)$海里的$B$处有一艘走私船，在$A$处北偏西$75^{\circ}$方向，距离$A$处$2$海里的$C$处的缉私船奉命以$10\sqrt{3}$海里/时的速度追截走私船，此时走私船正以$10$海里/时的速度从$B$处向北偏东$30^{\circ}$方向逃窜，问缉私船沿什么方向能最快追上走私船，并求所需时间。(注：$\sqrt{6}\approx 2.449$) 
设缉私船沿北偏东$\theta$的$CD$方向能最快追上，所需时间为$t$小时，并设$\angle DCB=\alpha$， 在$\Delta ABC$中，$AB=\sqrt{3}-1$，$AC=2$，$\angle BAC=120^{\circ}$， 则由余弦定理可知，$BC^2=AC^2+AB^2-2\cdot AC\cdot AB\cdot cos120^{\circ}=\cdots=6$，则$BC=\sqrt{6}$； 在$\Delta ABC$中，由正弦定理可知，$\cfrac{AC}{sin\angle CBA}=\cfrac{BC}{sin120^{\circ}}$，代值整理得到 $sin\angle CBA=\cfrac{\sqrt{2}}{2}$，则可知$\angle CBA=\cfrac{\pi}{4}$，即$B、C$两点在正东正西方向上。 在$\Delta BCD$中，$BC=\sqrt{6}$，$BD=10t$，$CD=10\sqrt{3}t$，$\angle CBD=120^{\circ}$， 则由余弦定理可知，$CD^2=BC^2+BD^2-2\cdot BC\cdot BD\cdot cos120^{\circ}$， 化简整理得，$200t^2-10\sqrt{6}t-6=0$，即$(20t+\sqrt{6})(10t-\sqrt{6})=0$， 解得$t=\cfrac{\sqrt{6}}{10}\approx 0.245$小时$=14.7$分钟。 此时，由正弦定理可得，$\cfrac{BD}{sin\angle DCB}=\cfrac{CD}{sin120^{\circ}}$，即$\cfrac{10t}{sin\alpha}=\cfrac{10\sqrt{3}t}{sin120^{\circ}}$， 代值整理得到，$sin\alpha=\cdots=\cfrac{1}{2}$，故$\alpha=30^{\circ}$。 即沿北偏东$60^{\circ}$或东偏北$30^{\circ}$方向能追上，最快用时约$14.7$分钟。
反思总结：①本题目的难点之一，就是根据题意做出图形，作图时需要理解题中的各种角的含义， ②且在$A、B、C$处需要建立方位。同时还存在做出的是俯视图还是斜二测图形。 ③题目一开始我们并不知道$BC$两点在正东正西方向上，所以直接设沿着东偏北多少是错误的。 ④在$\Delta BCD$中使用正弦定理求$sin\angle DCB$时，代入边长时要么都用边长，要么都使用速度，以减少运算错误；如果利用余弦定理计算$cos\angle DCB$会非常麻烦。001
如图，一条河的两岸平行，河的宽度\(d＝0.6 km\)，一艘客船从码头A出发匀速驶往河对岸的码头B。已知\(AB＝1km\)，水的流速为\(2 km/h\)，若客船从码头A驶到码头B所用的最短时间为\(6 min(0.1h)\)，则客船在静水中的速度为 【 】
A．\(8 km/h\) \(\hspace{2cm}\) B．\(6\sqrt{2} km/h\) \(\hspace{2cm}\) C．\(2\sqrt{34} km/h\) \(\hspace{2cm}\) D．\(10 km/h\)
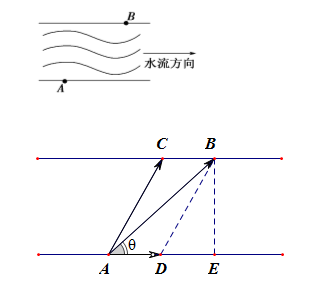
分析：此题涉及到运动的合成，如右图所示，要想使得船的最终实际航行路线是AB，那么船在静水中时的航线应该是AC，水流的方向是AD，这样在两个向量AC、AD的共同作用下，船的最终实际航行路线才可能是AB，这样就形成了\(\Delta ABC\)和\(\Delta ABD\)；
设客船在静水中的速度为\(v km/h\)，那么\(AC=BD=0.1v\)，\(AB=1\)，\(AD=0.1\times 2=0.2\)，
在\(\Delta BAE\)中，\(sin\theta=\cfrac{0.6}{1}=\cfrac{3}{5}\)，则\(cos\theta=\cfrac{4}{5}\)，即\(cos\angle BAD=cos\theta=\cfrac{4}{5}\)
则在\(\Delta ABD\)中，\(BD^2=AB^2+AD^2-2AB\cdot AD\cdot cos\angle BAD\)；
即\((0.1v)^2=1^2+(0.2)^2-2\times 1\times 0.2\times \cfrac{4}{5}\)，解得\(v=6\sqrt{2}\)，故选B。
002 一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100m 到达点B，在B点测得水柱顶端的仰角为 30°，则水柱的高度是【】
A．\(50m\) \(\hspace{2cm}\) B．\(100m\) \(\hspace{2cm}\) C．\(120m\) \(\hspace{2cm}\) D．\(150m\)
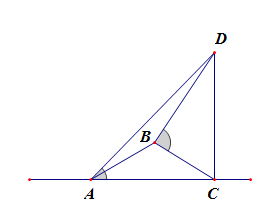
分析：本题目的难点是作出适合题意的立体图形，必要的时候可以使用斜二次画法理解题意。
如右图所示，水柱高为CD，其垂直于下底面ABC，
\(\angle DAC=45^{\circ}\)，\(\angle BAC=60^{\circ}\)，\(\angle DBC=30^{\circ}\)，
设水柱的高度为\(h\)，则在\(\Delta ABC\)中，\(BC=\sqrt{3}h\)，\(AC=h\)，\(AB=100\)，\(\angle BAC=60^{\circ}\)，
由余弦定理可得\(BC^2=AB^2+AC^2-2AB\cdot AC\cdot cos\angle BAC\)，
即\(3h^2=h^2+100^2-2\times 100\times h\times \cfrac{1}{2}\)，
化简整理得到，\(h^2+50h-5000=0\)。
解得\(h=-100(舍去)\)或\(h=50\)。故选A。
【例1】据气象部门预报，在距离某码头正西方向\(400km\)处的热带风暴中心正以\(20km/h\)的速度向东北方向移动，距离风暴中心\(300km\)以内的地区为危险区，该码头处于危险区内的时间是_____小时。
https://www.desmos.com/calculator/jnpmgjgnni
法1：解三角形法
设风暴移动的时间为\(t\)小时，由题可知，\(AB^2=400^2+400t^2-2\times20t\times400\cfrac{\sqrt{2}}{2}\leq 300^2\)，
解得$10\sqrt{2}-5\leq t \leq 10\sqrt{2}+5 $
所以码头处于危险区的时间为\(10\sqrt{2}+5-(10\sqrt{2}-5)=10\).
【难点列举】
1、转化为解三角形模型
2、\(AB^2 \leq 300^2\)的理解
3、解不等式，十字相乘法变换为公式法
4、对\(t=10\sqrt{2}\pm 5\)的理解
法2：平面几何法
分析：利用圆中的\(Rt\Delta\)可知风暴作用于码头的距离是\(200km\)，故时间为\(\cfrac{200}{20}=10\)小时。
【例2】立体图形中的方位角的问题
http://bmob-cdn-5522.b0.upaiyun.com/2017/04/10/95c02ba5408e0e858033c6be11b63609.html?s=share
