反三角函数、余弦定理求解角度问题—

反三角函数、余弦定理求解角度问题——计算不收敛

本文主要是介绍反三角函数、余弦定理求解角度问题——计算不收敛，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在三角形关系里求解角度时，我们一般采用余弦定理、反三角函数。假设三角形的三条边分别为a，b，c，其中a，b两个边的夹角为θ（未知），则夹角θ表示为：

$\theta =arccos\frac{a^{2}+b^{2}-c^{2}}{2*a*b}$

正常的三角形用我们已知的这种方法进行角度求解是没有任何问题的。但是，人生不会那么如意让你顺利的求得每一个想要的角度。于是会出现这样一种情况：

图源：知乎-生信洞

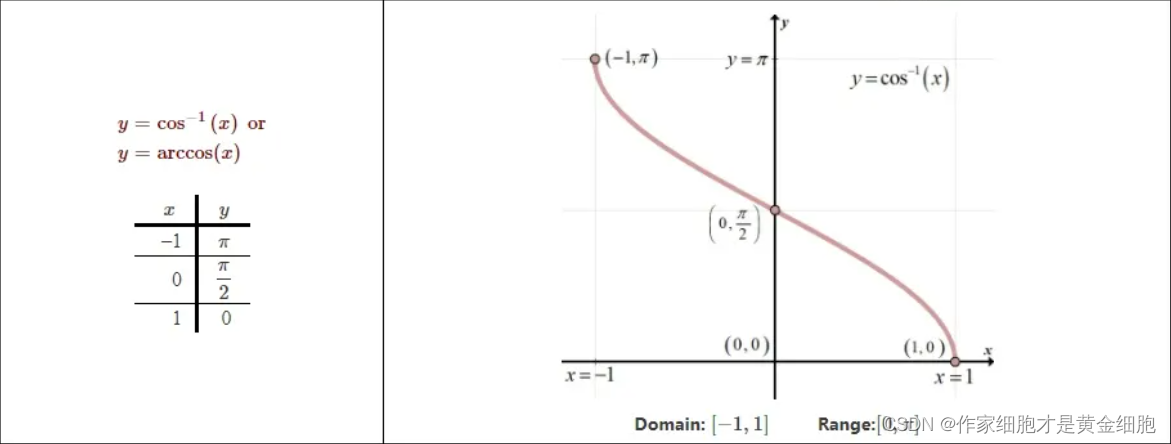
我们记x表示为：

$x=\frac{a^{2}+b^{2}-c^{2}}{2*a*b}$

从arccos函数图像可以看出，当x非常接近于1时，会出现斜率无穷大的情况。这导致计算机在进行运算时，反三角函数会出现计算不收敛的情况，说白了就是你根本求不到实际的角度θ。这里提供一种思路：

（来源CSDN-落叶无情：高精度反三角函数的实现_落叶无情的博客-CSDN博客）

$arccos(x)=arctan\frac{\sqrt{1-x^{2}}}{x}=arctan(y)$

$y=\frac{\sqrt{1-x^{2}}}{x}$

引入反三角函数的泰勒展开，我们可以计算角度θ为：

$\theta =arctany=y-\frac{1}{3}y^{3}+\frac{1}{5}y^{5}-\frac{1}{7}y^{7}\cdots$

这样就可以把反三角函数求解角度问题转换为幂次方的加减运算了，解决了反三角函数在值接近1时运算不收敛的问题。

其实反三角函数问题，归根结底为反正切函数问题，运用反三角函数之间的转换关系，可以把arccos中一个非常接近于1的值转换为arctan中<0.5的值，然后运用泰勒展开进行运算求解，一般计算到5次方得到的值已经很准确了。

这篇关于反三角函数、余弦定理求解角度问题——计算不收敛的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

反三角函数、余弦定理求解角度问题——计算不收敛