九讲专题
背包问题问法的变化(背包九讲)
前言: 以上涉及的各种背包问题都是要求在背包容量(费用)的限制下求可以取到的最大价值,但背包问题还有很多种灵活的问法,在这里值得提一下。但是我认为,只要深入理解了求背包问题最大价值的方法,即使问法变化了,也是不难想出算法的。例如,求解最多可以放多少件物品或者最多可以装满多少背包的空间。这都可以根据具体问题利用前面的方程求出所有状态的值(f数组)之后得到。还有,如果要求的是“总价值
有依赖的背包问题(背包九讲)
问题: 这种背包问题的物品间存在某种“依赖”的关系。也就是说,i依赖于j,表示若选物品i,则必须选物品j。为了简化起见,我们先设没有某个物品既依赖于别的物品,又被别的物品所依赖;另外,没有某件物品同时依赖多件物品。 算法: 这个问题由NOIP2006金明的预算方案一题扩展而来。遵从该题的提法,将不依赖于别的物品的物品称为“主件”,依赖于某主件的物品称为“附件”
分组的背包问题(背包九讲)
问题: 有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。 算法: 这个问题变成了每组物品有若干种策略:是选择本组的某一件,还是一件都不选。也就是说设f[k][v]表示前k组物品花费费用v能取得的最大权
背包九讲笔记-完全背包问题
基本思路 完全背包就是01背包的变化,所有的物件不再是单一的,而有无限个,可以先用01背包的思路,让所有的每种物品都装尽量多,那么我们可以获得状态转移方程: F[i,v] = max{F[i − 1,v],F[i − 1,v − kCi] + kWi| 0 ≤ kCi≤ v} 或者是: F[i,v] = max{F[v],F[v − kCi] + kWi| 0 ≤ kCi≤ v} (优化
背包九讲笔记-01背包问题
基本思想 与动规类似,把大问题分解,把因为求第i个物品放入背包的获利会受到第i-1个物品的影响,因此,需要考虑其影响,即考虑第i-1个物品获利。然后在剩余空间允许的情况下,再考虑将第i个物品放入后的获利并与前比较,这样,就获得了状态转移方程: F[i,v] = max{F[i − 1,v],F[i − 1,v − Ci] + Wi}。 这样的常规思路需要一个DP二维数组来记录(以体积为标准)
dd大牛的《背包九讲》
P01: 01 背包问题 题目 有 N 件物品和一个容量为 V 的背包。第 i 件物品的费用是 c[i] ,价值是 w[i] 。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。 基本思路 这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。 用子问题定义状态:即 f[i][v]
【C++算法模板】背包九讲(下):混合背包、二维费用背包、带依赖的背包、背包求方案数、背包求具体方案
文章目录 1)混合背包2)二维费用背包3)带依赖的背包4)背包求方案数5)背包求具体方案 1)混合背包 时间复杂度: O ( n 2 l o g 2 ) O(n^2log^2) O(n2log2),空间复杂度: O ( n ) O(n) O(n) 关键点在于将多重背包二进制优化后变成 01 01 01背包和 01 01 01背包一起处理,完全背包单独处理,其实就是混
【背包九讲】01背包问题
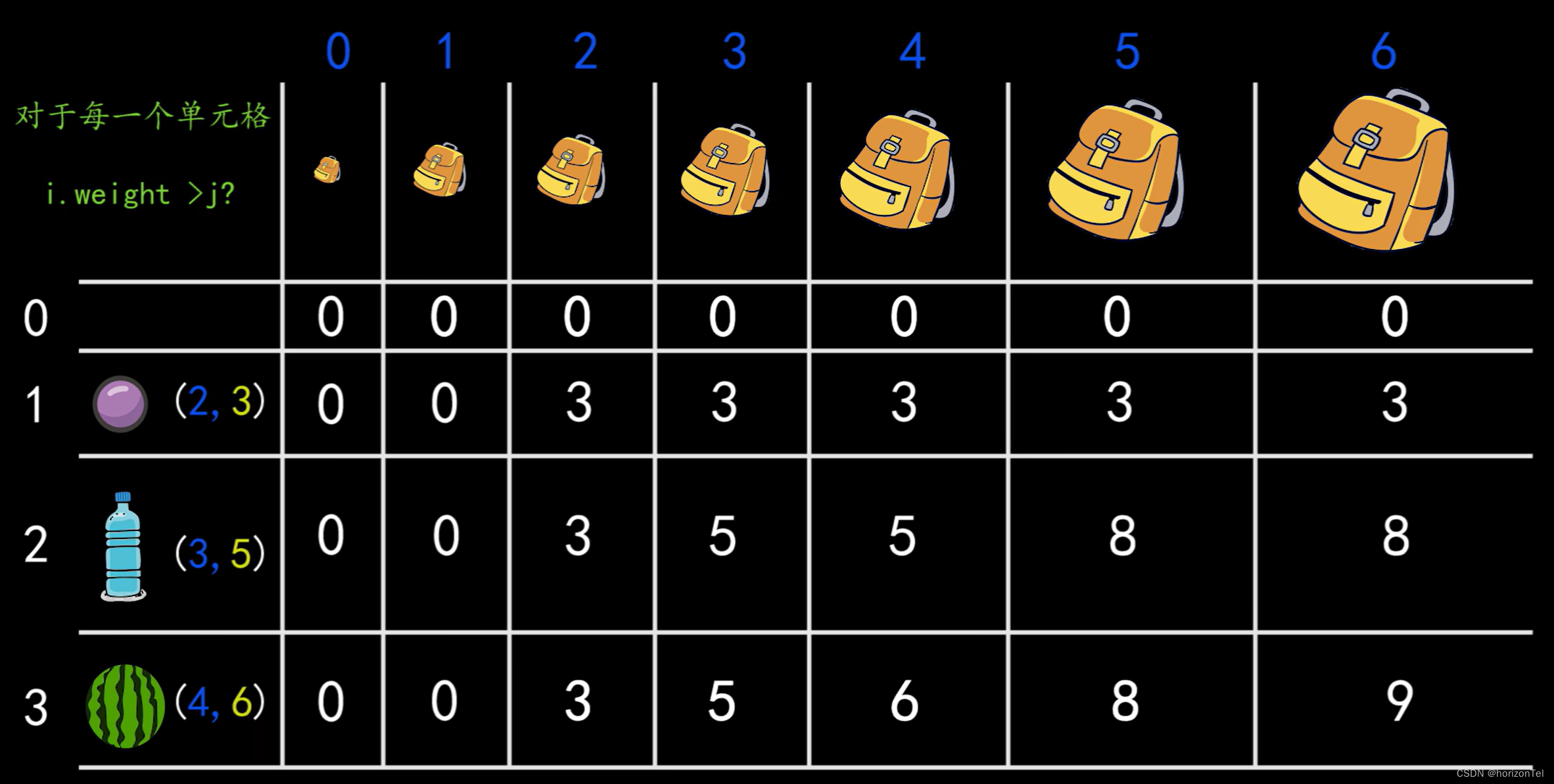
1、01背包问题描述 已知:有 N 件物品和一个容量为 V 的背包。第i件物品的重量为w[i],得到的价值是 c[i]. 问题:求解将哪些物品装入背包可使价值总和最大。 条件:每种物品只有一件,可以选择放或者不放 2、基本思路 01背包的特点:每种物品只有一件,可以选择放或者不放 子问题定义状态 F[i][v] :前i件物品放到一个容量为V的背包中的最大价值 状态转移方程 F[i]
背包九讲——多重背包
多重背包,每件物品能选的数量有限制,最多c【i】个 1.二进制优化: 二进制优化的思想还是很巧妙的,根据c【i】得到一组这样的数 2^0,2^1,2^2,2^3.....2^(k-1) , c-2^k+1 其中k是满足2^k小于c的最大值,就像c=7=111,2^k=100=4 ; c=9=1001, 2^k=1000=8 ; c=8=1000 2^k=0100=4 得到
背包九讲——完全背包
P02: 完全背包问题 题目 有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。 基本思路 这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很多种。如果仍然按
背包九讲——01背包(降维+常数级优化)
题目: 共n个物体,第i个重量为w[i],价值v[i],背包最多能背不超过W的物体,求最大的价值 分析: 每个物体只有一个,在容量允许时(W>w[i]),则对于每个物体只有取、不取两种选择 状态:dp[i][j]:前i个物体,在容量为j的时候,最大的价值 状态转移: dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[
P1439 背包九讲(1):简单的0-1背包
P1439 背包九讲1:简单的0-1背包 一、原题呈现1、题目描述2、输入描述3、输出描述4、样例输入5、样例输出 二、思路分析这是一个最基础的01背包问题。 三、整体代码 一、原题呈现 1、题目描述 有一个箱子容量为 V(正整数,0<=V<=20000),同时有 n 个物品(0<n<=30),每个物品有一定的体积和价值。要求 n 个物品中,任取若干个装入箱内,在箱子能放得下的
算法整理 复习:背包九讲
文章目录 一、01 背包二、完全背包三、多重背包3.1 普通多重背包3.2 二进制优化多重背包3.3 单调队列优化多重背包 一、01 背包 01背包问题 #include <stdio.h>#include <iostream>using namespace std;#define MAXN 1005int n, m;int bag[MAXN];in