之红专题

二叉搜索树进阶之红黑树

前言：在上文我们已经学习了AVL树的相关知识以及涉及的四种旋转的内容，但是AVL树追求平衡导致旋转操作过多，一些情况下影响性能，由此我们就来了解一下二叉搜索树的另外一个分支，红黑树。（倘若对旋转知识不了解的可以先移步：http://t.csdnimg.cn/waigV）红黑树的概念：红黑树是一种二叉搜索树，通过对每个节点增加一个存储位表示节点的颜色，（红色或者黑色），再通过对任何一

数据结构复习指导之红黑树

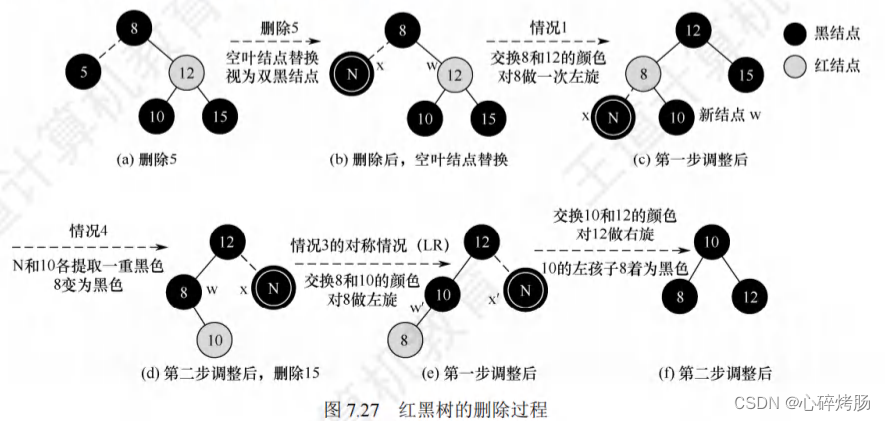
目录红黑树考纲内容知识框架复习提示 1.红黑树的定义 2.红黑树的插入 3.红黑树的删除归纳总结红黑树考纲内容（一）查找的基本概念（二）顺序查找法（三）分块查找法（四）折半查找法（五）树形查找二叉搜索树；平衡二叉树；红黑树（六）B树及其基本操作、B+树的基本概念（七）散列(Hash)表（八）查找算法的分析及应用

数据结构之红黑树——BST的变种2

转自：http://hxraid.iteye.com/blog/611816 感谢原文作者的分享红黑树的性质与定义红黑树(red-black tree) 是一棵满足下述性质的二叉查找树： 1. 每一个结点要么是红色，要么是黑色。 2. 根结点是黑色的。 3. 所有叶子结点都是黑色的（实际上都是Null指针，下图用NIL表示）。叶子结点不包含任何关键字信

数据结构之红黑树——BST的变种

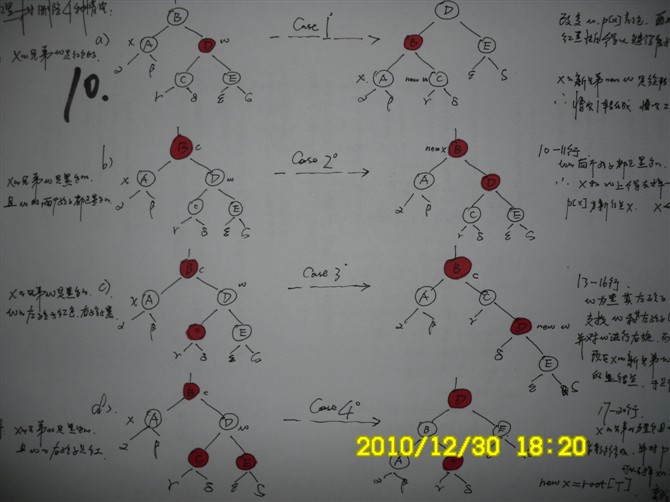
转自大神July的博客：点击打开链接在此mark一下教你透彻了解红黑树作者：July、saturnman 2010年12月29日本文参考：Google、算法导论、STL源码剖析、计算机程序设计艺术。推荐阅读： Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wad

C++AVL树拓展之红黑树原理及源码模拟

前言：我们之前已经从零开始掌握AVL树http://t.csdnimg.cn/LaVCChttp://t.csdnimg.cn/LaVCC 现在我们将继续学习红黑树的原理并且实现插入等功能，学习本章的前提要求是掌握排序二叉树和AVL树，本章不再提及一些基础知识，防止本文结构臃肿，对二叉排序树和AVL树有兴趣的可以阅读上面链接的文章，很多人可能说既生瑜何生亮，有了AVL树为什么还要红黑树，当然是因

数据结构之红黑树（二）——插入操作

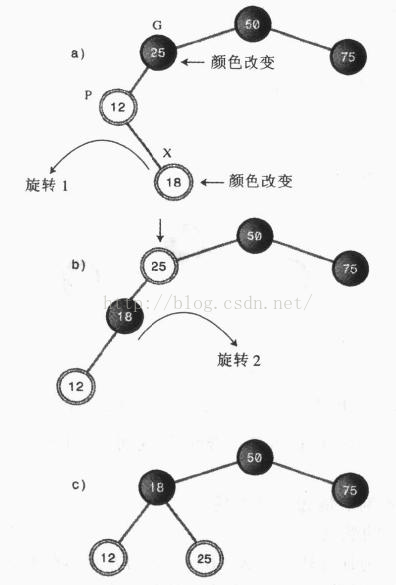
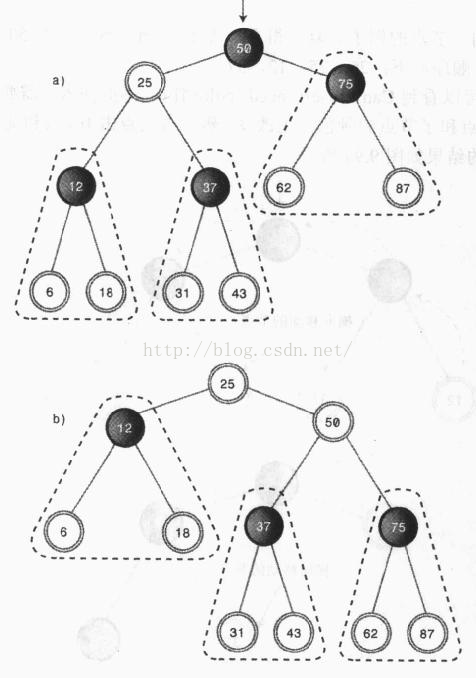
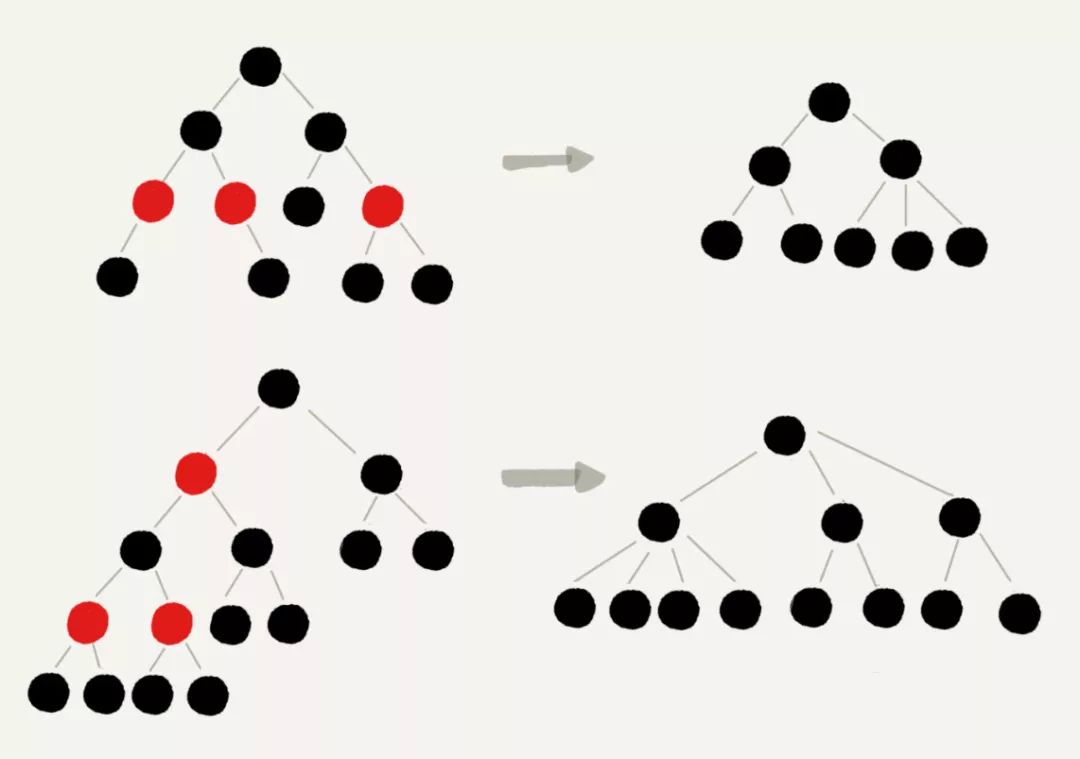
插入或删除操作，都有可能改变红黑树的平衡性，利用颜色变化与旋转这两大法宝就可应对所有情况，将不平衡的红黑树变为平衡的红黑树。在进行颜色变化或旋转的时候，往往要涉及祖孙三代节点：X表示操作的基准节点，P代表X的父节点，G代表X的父节点的父节点。我们先来大体预览一下插入的过程： 1、沿着树查找插入点，如果查找过程中发现某个黑色节点的两个子节点都是红色，则执行一次颜色变换（父节点变为红

数据结构之红黑树（一）——基础分析

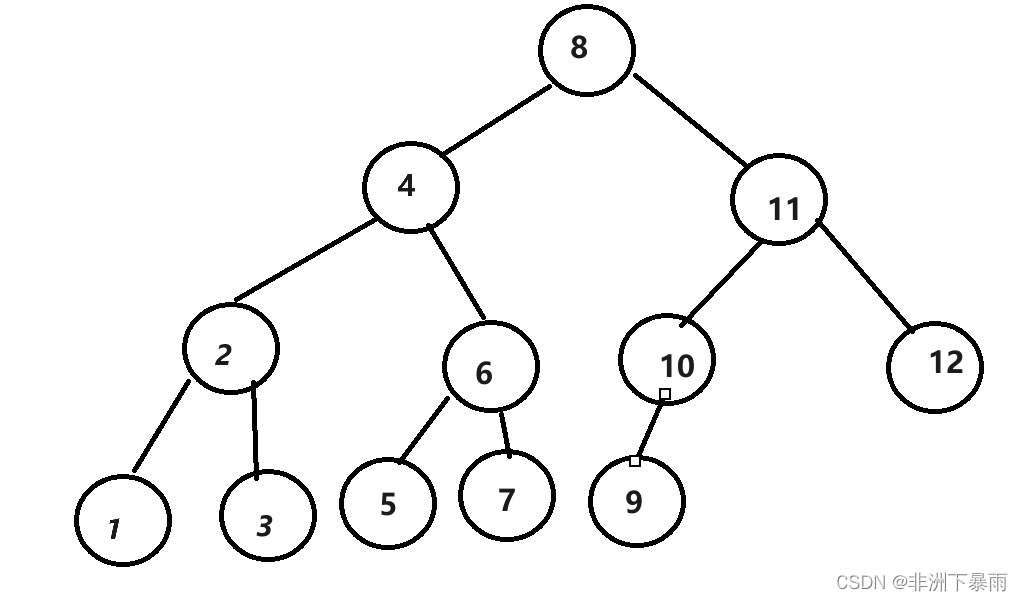
在二叉树中已经探讨过，如果按照随机顺序插入树节点，绝大多数都会出现不平衡的情况。最坏的情况，插入的数据时有序的，二叉树将会变成链表，插入、删除的效率将会严重地降低下图就是按照数据升序的顺序插入二叉树的情况：红黑树就是一种解决非平衡树的方法，它是增加了某些特点的二叉搜索树为了能较快的时间来搜索一颗树，需要保证树总是平衡的（或者至少大部分是平衡的），就是说对树中的每个节点，

数据结构之红黑树：为什么工程中都用红黑树这种二叉树？

上两节，我们依次讲了树、二叉树、二叉查找树。二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是 O(logn)。不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 log2n 的情况，从而导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。我上一节说了，要解决这个复杂度

数据结构之红黑树，二进制的奇妙冒险！

目录简述 1. 何为红黑树 2. 红黑树由来 3. 树平衡手段 4. 平衡因子 5. 增删节点逻辑 1. 增加节点 2. 删除节点 6. 红黑状态 1. 平衡限制带来的优化 2. 相对深度计算 3. 旋转的红黑状态变化 4. 删除的红黑状态变化 5. 惰性检查 Cheers！要说在程序员间广为人知而又颇具难度的数据结构，红黑树算是响当当的一号人物。如果

数据结构之红黑树（图文并茂版、一篇足够版）

为什么会出现红黑树红黑树的原理网络上关于红黑树的资料很多，但是总是上来就给出红黑树的特点，弄的人云里雾里，索性自己学习整理，写一篇较为完整的红黑树文章，文章从上面二个标题来展开，首先介绍红黑树的由来。红黑树动态插入演示红黑树的由来你应该听说过：二叉树、平衡二叉树、B树、B+树、红黑树。说到底红黑树还是一种二叉树，是为了解决普通树存在的问题而诞生的。先来看二叉树 1.左子树上所

基本数据结构之红黑树

红黑树红黑树（Red-Black Tree，R-B Tree）是一种自平衡的二叉查找树。在红黑树的每个节点上都多出一个存储位表示节点的颜色，颜色只能是红（Red）或者黑（Black）。是根据AVL树进化而来的，由于AVL树每次插入都需要动态调整，这需要大量的时间，因此出现了红黑树。红黑树不会像AVL树那样，每次插入都需要动态调整。因此当数据经常变化的时候，红黑树的效率要比AVL树要高。