数据结构之红黑树（图文并茂版、一篇足够版）

• 为什么会出现红黑树
• 红黑树的原理

网络上关于红黑树的资料很多，但是总是上来就给出红黑树的特点，弄的人云里雾里，索性自己学习整理，写一篇较为完整的红黑树文章，文章从上面二个标题来展开，首先介绍红黑树的由来。
红黑树动态插入演示

红黑树的由来

你应该听说过：二叉树、平衡二叉树、B树、B+树、红黑树。
说到底红黑树还是一种二叉树，是为了解决普通树存在的问题而诞生的。
先来看二叉树

1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。

二叉树的本质是进行二分查找，具有优越的查找性能。对于普通的二叉树，我们按顺序插入9、8、7、6、5、4、3、2、1会出现什么情况呢？

根据二叉树原理来插入，这棵树会显得很不平衡，其查找性能随之下降，这里我要查找3，几乎是线性遍历了。所以，在普通二叉树的基础上，我们还需要一定的理论，让树可以自己保持平衡，于是出现了AVL树，也就是平衡二叉树。平衡二叉树的理论可以让我们再插入图二的数据时，生成一个图一中的数据结构。AVL是一颗完美平衡的树，非常好非常理想化，但实际数据结构中我们仿佛听到的更多的是红黑树，为什么？
简而言之是，AVL具有完美的查找性能，但进行插入、删除时，需要进行的旋转操作次数不可控，有些效率问题。但红黑树保证的不是完美平衡，而是比较平衡，提高了插入、删除节点的效率，而查找性能并没有降低(红黑树log2N，AVL树logN)，任何不平衡都会在三次旋转之内解决。所以实际工程中使用红黑树较多。

红黑树的原理

为了保证大致平衡这个理念，这才有了下面这几个到处都有的红黑树性质。

1.　根节点是黑色的；
2.　每个叶子节点都是黑色的空节点，也就是说，叶子节点不存储数据；
3.　任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
4.　每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

为什么要有颜色区分？为了限制旋转次数。当颜色满足时就可停止旋转，当然节点的值也是影响旋转的因素之一。我们看下面这个例子：
插入3，此时3是黑色

插入1，此时1是红色

插入2，经过两次旋转，如下几步
第一步：

根据规则，插入的2是红色，不满足规则3
第二步：

不满足规则3
第三步：

不满足规则3，改变颜色
第四步：

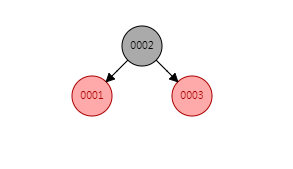
这时我们继续插入4，会发生什么事情？



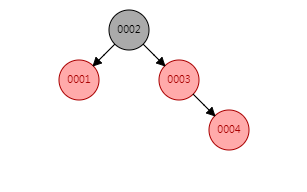
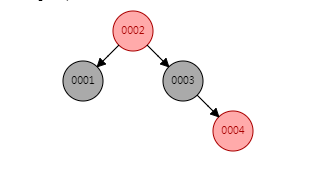
到这里基本是按照规则进行改变颜色，为了形象说明红黑树中颜色的作用，我们用AVL平衡树来做一个对照，在后面数据插入的过程中，会看到这个变化。
从001-004这个过程是一样的，用同样的办法构建一个AVL树：

接着看如下变化，插入节点5，在结构上看不出什么，但是平衡树进行的遍历次数要比红黑树多了。

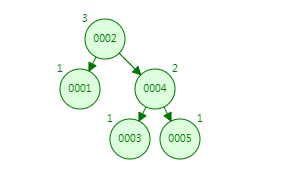
接着插入006

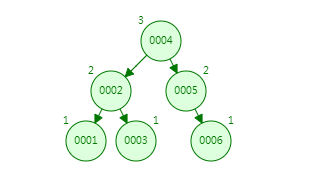
经过对比，此时已经能看出变化，红黑树只是继续在005后追加006，而平衡树却经过遍历，进行了一次旋转。
具体的动画效果包含的信息也非常丰富

红黑树可视化
AVL树可视化
说真的这里不得不吐槽，我们国家的计算机教育怎么没有这么好的学习资源，这么好的学习资源甚至还没有普及，还很少人知道。

经过动画展示，以及可以看出来，红黑树的插入效率要比AVL树高，但不绝对平衡这件事。

下面我们看一下jdk1.8中，HashMap在处理hash冲突使用的红黑树源码。

红黑树源码

位置：HashMap.class 2214行开始
这里是红黑树的插入方法

        static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {//新插入的节点为红色x.red = true;//定义变量和循环//xp：当前节点的父节点//xpp：爷爷节点//xppl：左叔叔节点，这里的变量名起的不好，应该是xpl更合适，下同//xppr：右叔叔节点for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {//如果当前节点父节点为空，直接返回插入的x，并置成黑色（false），说明白点就是插入第一个节点if ((xp = x.parent) == null) {x.red = false;return x;}//如果父节点不是红色或爷爷节点不为空，直接返回根节点。基本上是插入第二行和其他不需要变换的情况。请见下注释一说明情况。else if (!xp.red || (xpp = xp.parent) == null)return root;// 如果父节点是爷爷节点的左孩子Condition_1（和下面Condition_2对应），见注释二if (xp == (xppl = xpp.left)) {//Condition_1_1 如果其右叔叔不为空，且为红色，则改变右叔叔的颜色，改变父亲的颜色，改变爷爷的颜色，见注释二if ((xppr = xpp.right) != null && xppr.red) {xppr.red = false;	//叔叔节点置黑xp.red = false;		//父亲置黑xpp.red = true;		//爷爷置红x = xpp;			//进入下一次循环}//Condition_1_2 右叔叔为空 或者 为黑色else {// 如果当前节点是父节点的右孩子	Condition_1_2_1，见注释三if (x == xp.right) {// 父节点左旋root = rotateLeft(root, x = xp);// 见注释三xpp = (xp = x.parent) == null ? null : xp.parent;}// 如果父节点不为空 Condition_1_2_2 ，见注释三if (xp != null) {xp.red = false;if (xpp != null) {xpp.red = true;root = rotateRight(root, xpp);}}}}// 如果父节点是爷爷节点的右孩子Condition_2else {// 如果左叔叔是红色 Condition_2_1if (xppl != null && xppl.red) {xppl.red = false;// 左叔叔置为 黑色xp.red = false;// 父节点置为黑色xpp.red = true;// 爷爷置为红色x = xpp;// 运行到这里之后，就又会进行下一轮的循环了，将爷爷节点当做处理的起始节点}// 如果左叔叔为空或者是黑色Condition_2_2else {// 如果当前节点是个左孩子 Condition_2_2_1if (x == xp.left) {// 针对父节点做右旋root = rotateRight(root, x = xp);xpp = (xp = x.parent) == null ? null : xp.parent;}//Condition_2_2_2if (xp != null) {xp.red = false;if (xpp != null) {xpp.red = true;// 针对爷爷节点做左旋root = rotateLeft(root, xpp);}}}}}}

源码是左右互偶的，不太明白网上说红黑树最多旋转3次以内。通过阅读源码可以看出来，判断是否旋转的条件包括节点颜色、节点的左右性，节点是否为空三种条件。

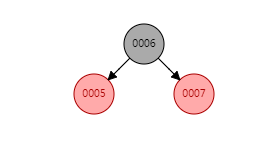
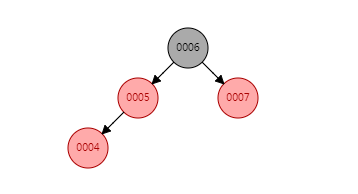
上面我们有张图

这时如果插入007节点会发生什么事？
首先007是006的右子节点，且父节点为爷爷节点右孩子，直接进入Condition_2_2_2，一次旋转，父节点和爷爷节点变色即可。我们看结果



以上

注释一

条件一 !xp.red有这样一颗树，现在要插入一个大小为0.9的节点


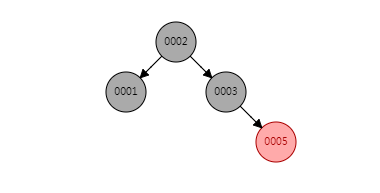
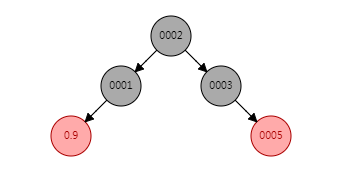
我们会发现，当父节点为黑色，是可以直接插入，且不用旋转的。
条件二 (xpp = xp.parent) == null
初始树：

插入001

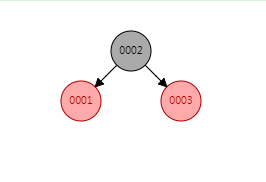
这种情况直接可以插入成功，不需要变换。所以可以直接返回root（该函数的返回值就是返回当前树的root节点）

注释二

有如下初始树

现在要插入004，则4的父亲005节点是其爷爷节点（006）的左孩子，满足该条件

xp == (xppl = xpp.left)

然后这里也满足第二个条件Condition_1_1

xppr = xpp.right) != null && xppr.red

现在插入004，按照代码里的规则，会改变007的颜色为黑，005的颜色黑，006的颜色为红。我们看动画分解：


完全按照代码的逻辑实现的，但是真里有人问了，006根节点不应该是黑色么，注意看这里面的代码是一个for循环，改变颜色后并没有return，而是进入下一次循环，第二次就会将爷爷节点当作当前处理的节点来处理，也就是006，然后就会执行注释一的逻辑，将其置黑，并return。

if ((xp = x.parent) == null) {x.red = false;return x;
}

注释三

Condition_1_2_1 如果当前节点是父节点的右孩子
初始化树

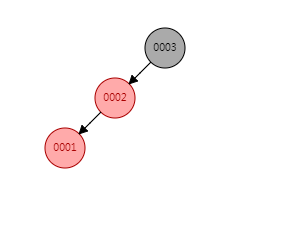
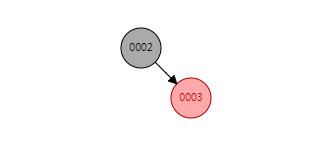
现在要插入003，003的位置会在002的右侧（永远往叶节点插入数据，然后再旋转）

条件满足了，这时候父节点左旋

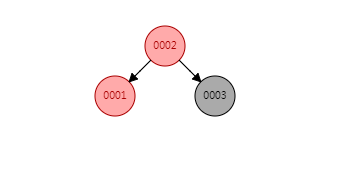
进入下一个条件，此时002满足Condition_1_2_2，

将父节点置黑，爷爷节点置红，爷爷节点右旋转