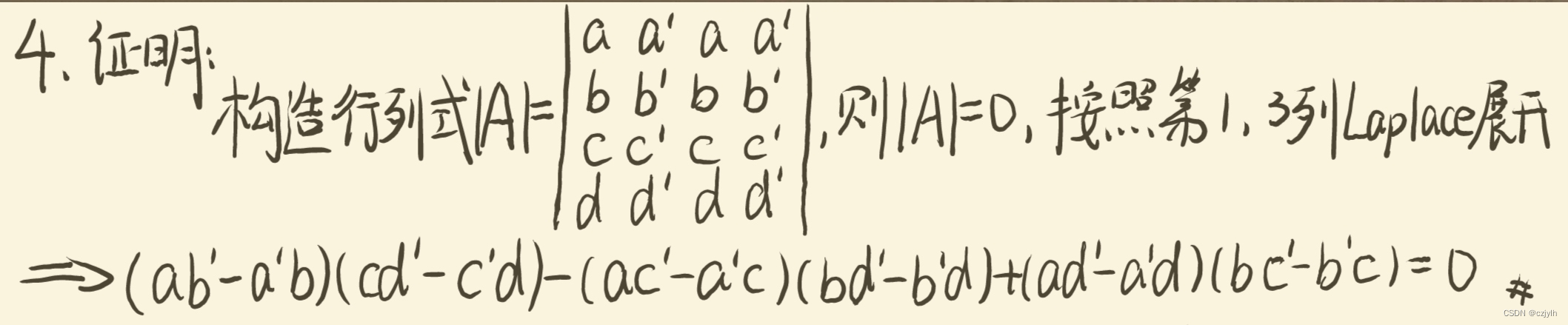t4专题
第T4周：猴痘病识别
本文为🔗365天深度学习训练营 中的学习记录博客原作者：K同学啊 我的环境： ● 语言环境：Python3.6.5 ● 编译器：jupyter notebook ● 深度学习框架：TensorFlow 2.6.2 ● 数据：猴痘病数据集 一、前期工作 设置GPU（如果使用的是CPU可以忽略这步） from tensorflow import kerasfrom ten
林昊：用淘宝T4保障系统稳定性 降低运维成本
阿里巴巴高级技术专家林昊（腾讯科技配图） 腾讯科技讯 10月27日消息，2012全球软件开发大会（杭州站）进入第三天议程，阿里巴巴高级技术专家林昊在会上发表主题演讲，分享“T4：淘宝私有云”。 林昊介绍，淘宝在2011年开始引入虚拟化，引入以后，淘宝整个运维成本下降许多。他指出，许多企业运维成本不够低的主要原因包括：单台物理机上跑的应用不够多；分给应用的机型以及机器数是静态的；集群的
腾讯T4架构师用这12张手绘图，轻松带你搞懂微服务架构！太厉害了
微服务的概念最早在 2012 年提出，在 Martin Fowler 的大力推广下，微服务在 2014 年后得到了大力发展。今天我们通过一组手绘图来梳理下微服务的核心架构。 什么是微服务？ 微服务 Microservices 之父，马丁.福勒，对微服务大概的概述如下： 就目前而言，对于微服务业界并没有一个统一的、标准的定义（While there is no precise defin
Nanopc T4 使用OpenCV
识别长方形： import cv2import cv2 as cvimport timeimport platformimport os# 获取操作系统类型os_type = platform.system()if os_type == "Windows":# Windows系统cap = cv.VideoCapture(0) # 使用第零个摄像头elif os_type ==
第五届上海市青少年算法竞赛 T4 夹心饼干（思维、数学）
第四题：T4夹心饼干 标签：思维、数学题意：给定一个数列 a 1 , a 2 , a 3 . . . , a n a_1,a_2,a_3...,a_n a1,a2,a3...,an，请求出在这个序列中，能挑出多少个三个数 a i , a j , a k a_i,a_j,a_k ai,aj,ak，满足 i < j < k i<j<k i<j<k且 a i = a k a_i=a_k
国产化服务器透传NVIDIA TESLA T4卡
国产化服务器 最近玩了玩GPU卡在鲲鹏920处理器上的透传测试，记录一下测试的结果。 测试准备 拿到服务器配上带外，看一下服务器的型号，验证是真的国产化不是x86 既然都拿到了国产化服务器了，不如操作系统也用国产化的银河麒麟v10 SP1: 银河麒麟官方网站，想了解国产化操作系统可以看看.来搞吧😎使用lscpu看一下我们的Model确实是kunpeng-920。 鲲鹏920处理器，基于7
上海计算机学会2021年1月月赛C++丙组T4三倍游戏
题目描述 三倍游戏是一种单人游戏。玩家会得到 n 个整数a1,a2,…,an。玩家从这些整数中挑出两个数字相加，如果它们的和是 3 的倍数，则可以将这两个整数消除，如此反复，直到不能再消除数字为止。 请问玩家最多能消除多少对数字？ 输入格式 第一行：单个整数 n； 第二行：n 个整数a1,a2,⋯,an。 输出格式 单个整数表示答案。 数据范围 1≤ai≤1,000,
【Tesla T4为例】GPU安装最新版本NVIDIA Driver、CUDA、cuDNN、Anaconda、Pytorch
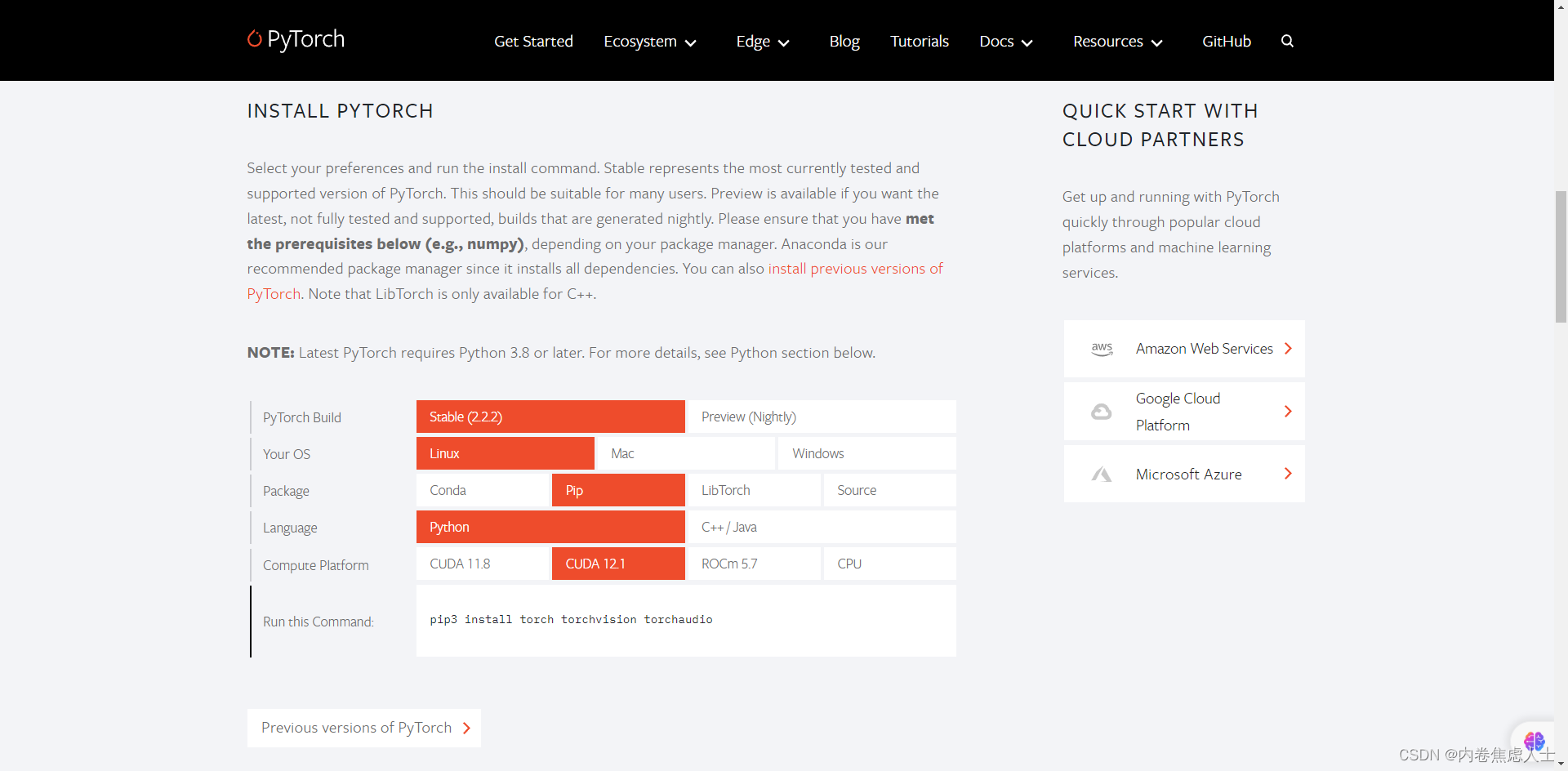
NVIDIA Driver 进入英伟达官网下载页面 按照以上方式选择即可得到>535.113.01版本的驱动，可以实现多卡推理，小于这个版本会导致多卡训练以及推理报错 虽然最新版本为550.54.15，但是535版本更加稳定，并且pytorch目前只支持到12.1，而在CUDA Toolkit选择栏中没有这个版本，所以选择12.2最稳妥 下载后上传至服务器，在安装驱动前先安装一些依赖 su
上海计算机学会 2023年9月月赛 乙组T4 组合数（组合数学）
第四题：T4组合数 标签：组合数学题意：求组合数 C n m C_n^m Cnm，即从 n n n个不同的数字中取出 m m m个数字的方案数，结果对 1 , 000 , 000 , 007 1,000,000,007 1,000,000,007取模（ 1 ≤ m ≤ n ≤ 1 0 9 ， 1 ≤ m ≤ 1 0 6 1≤m≤n≤10^9，1≤m≤10^6 1≤m≤n≤109，1≤m≤106
上海计算机学会 2024年3月月赛 丙组T4 交易记录（map）
第四题：T4交易记录 标签： m a p map map题意：给定 n n n条股票买入卖出操作，有对应的交易单价 a i a_i ai和交易数量 b i b_i bi，分别将多笔买入卖出交易价格相同的进行交易数量合并。买入记录按照交易价格从低到高排序，卖出记录按照交易价格从高到低排序。题解：按照题意进行模拟，分买入和卖出两种情况，可以通过两个结构体分别进行存储，存储之后分别按照题目中给定的
7038 -- 【11.18测试】t4
7038 – t4 这不是跳舞增强版吗 考虑把原来两种做法优化 分治 单组询问分治，对于每一层处理经过当前层mid的区间贡献 预处理[l,mid]的后缀min和max，枚举右端点，对于[mid+1,r]的min和max是确定的，分类讨论拼起来的区间的min和max在哪一边 发现对于min和max都各有一个分界点k ∀ i ∈ [ k , m i d ] ， m i n [ i , r
![洛谷 P8816 [CSP-J 2022] 上升点列（T4）](https://img-blog.csdnimg.cn/direct/349698c7aee64e61b526f485ea5a966a.png)
洛谷 P8816 [CSP-J 2022] 上升点列（T4）
目录 题目传送门 算法解析 最终代码 提交结果 尾声 题目传送门 [CSP-J 2022] 上升点列 - 洛谷https://www.luogu.com.cn/problem/P8816 算法解析 k = 0 且 xi, yi 值域不大时，这题是非常简单的 DP，类似「数字三角形」。 记 dp(x,y) 为「以 (x,y) 为终点，最长合法序列的长度」。 则对于所
高代绿皮第四版课后习题1.7 T4
原题 利用行列式及Laplace定理,证明下列恒等式: 解析 思路: 根据需证明的式子构造行列式如下 由于 中第1,3列相同,故 再按照第1,3列进行Laplace展开即可证得结论 参考解题细节：
高代绿皮第四版课后习题1.6 T4
原题 若一个n阶行列式中零元素的个数超过 个,证明: 这个行列式的值为0 解析 思路: 由于n阶行列式共有 个元素,若零元素个数大于 个,则非零元素至多为 个 但n阶行列式有n行n列,故可知 中至少有一个为0 根据行列式的组合定义可得 参考解题细节:
Test in 01.22 T4:pogo
这是道很有意思的模拟题。 首先，sro XF orz 题面： 首先想到的是暴力的算法，枚举每一步操作中最顶端的数字，然后在加上顶端数字，但具体的暴力做法是需要一定的思路的，因为骰子中每一面所对的面都是固定的，所以只需要确定上，前，右三个面就可以确定所有面上的数字，然后一一枚举即可：关键代码如下： 1 #include<cstdio> 2 #include<iostre
noip15年普及组-T4-推销员
题目:推销员 1. 60分解法 枚举+模拟 提出一个命题： 如果 X = 1 X=1 X=1， 走过的结点集合为 { i 1 } \{i_1\} {i1}， 如果 X = 2 X=2 X=2， 走过的结点集合为 { i 1 , i 2 } \{i_1, i_2\} {i1,i2} 就是说： X = 2 X=2 X=2的集合必然包含 X = 1 X=1 X=1的集合 证明: v[i] ：
NOIP2012 普及组 T4 文化之旅
文化之旅 （NOIP2012 普及组 T4 ） 题目描述 有一位使者要游历各国，他每到一个国家，都能学到一种文化，但他不愿意学习任何一种文化超过一次（即如果他学习了某种文化，则他就不能到达其他有这种文化的国家）。不同的国家可能有相同的文化。不同文化的国家对其他文化的看法不同，有些文化会排斥外来文化（即如果他学习了某种文化，则他不能到达排斥这种文化的其他国家）。现给定各个国家间的地理关系，各个
T4（文本模板转换工具包）代码生成-最佳保存的Visual Studio秘密
Rob beat me to it. Blogging about T4 (the Text Template Transformation Toolkit) had been on my list literally for a year. He and I were singing its praises last night. Hopefully I can add something s
使用T4模板根据数据库生成model层
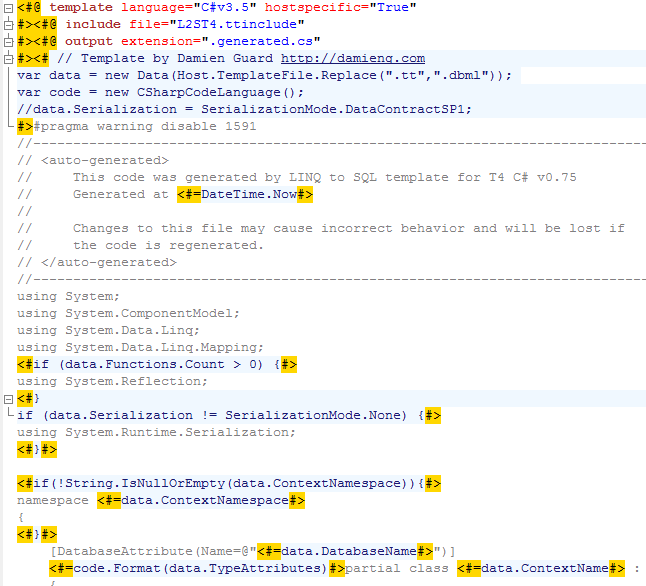
前言主要内容 T4模板介绍添加生成文件ManagerttincludeT4内代码 总结 前言 学习EF时接触到T4模板，感觉到了它的强大。既然EF的edmx文件下的tt文件可以生成model层的cs文件，那么我们也可以直接用T4模板生成model层喽。当然T4可以做更多事，不过今日我们只让它做这一件事。 本文主要参考以下文章： MVC —- Manager.ttinclu
CentOS7.4安装Nvidia Tesla T4驱动
环境:HPE 380 G10服务器，操作系统：CentOS7.4，显卡型号：Nvidia Tesla T4 步骤: 1.获取显卡型号 想办法获取自己的Nvidia显卡型号（一般显卡背面有），本人的显卡是Nvidia Tesla T4。 2.去NVDIA driver search page查看支持显卡的驱动最新版本及下载，下载之后是.run后缀。 3.把驱动文件拷贝到/tmp目
用google colab t4部署phi2（公网可访问）
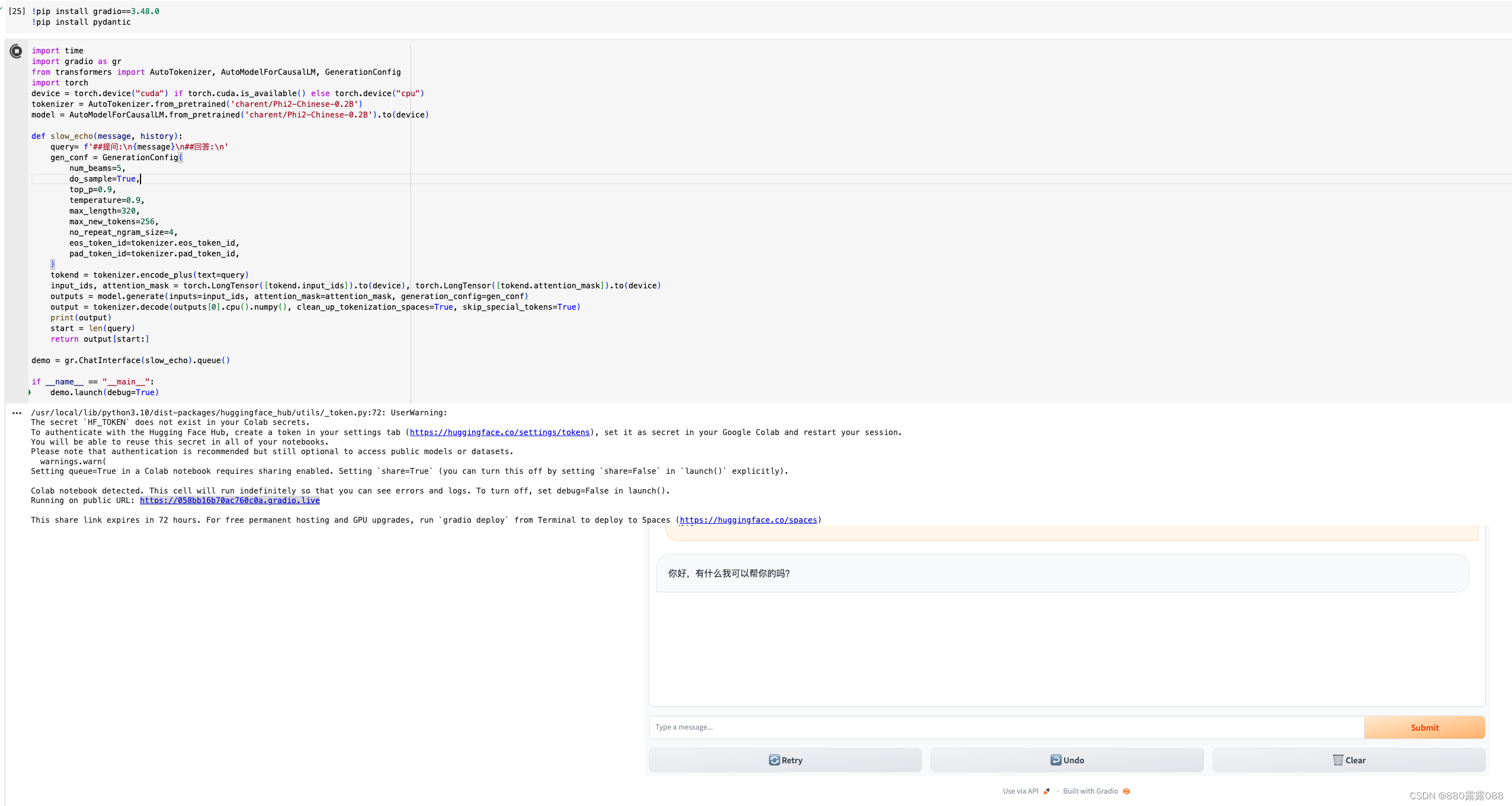
目录 1.打开google colab，配置GPU 2.ngrok获取authtoken 3.安装所需的包编辑 4.运行推理服务，生成公网地址 5.client.py访问上述推理服务 6.gradio界面版 1.打开google colab，配置GPU 2.ngrok获取authtoken https://dashboard.ngrok.com/get-starte
Oracle T4-4小型机上配置Ldom部署rac
Ldom控制域配置 (两台主机一样，以hydb1为例) root@hydb1 # ldm add-vds primary-vds0 primary root@hydb1 # ldm add-vcc port-range=5000-5100 primary-vcc0 primary root@hydb1 # ldm add-vsw net-dev=igb0 primary-vsw0 primary
20231222给NanoPC-T4(RK3399)开发板的适配Android11的挖掘机方案并跑通AP6398SV
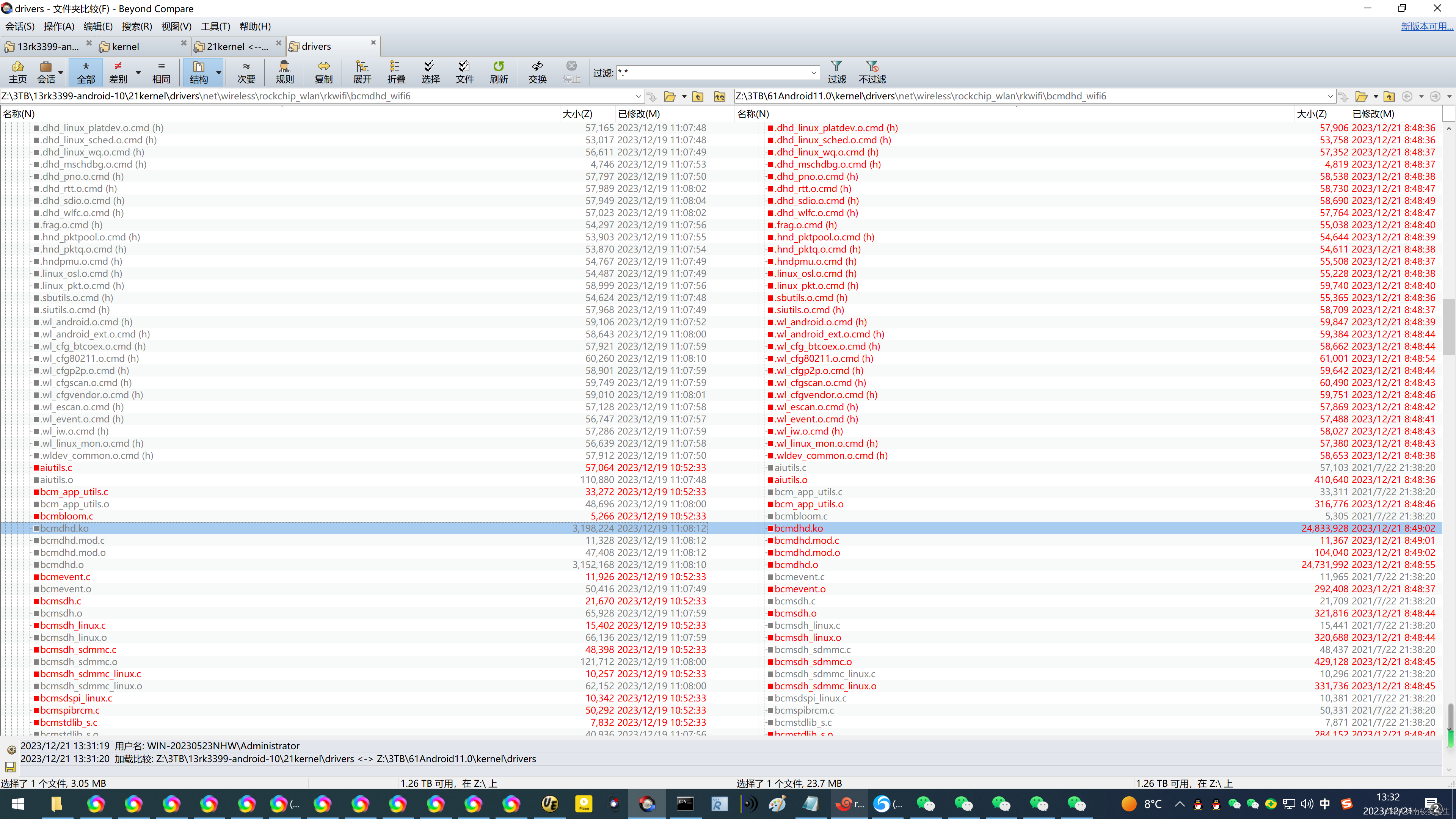
20231222给NanoPC-T4(RK3399)开发板的适配Android11的挖掘机方案并跑通AP6398SV 2023/12/22 7:54 简略步骤：rootroot@rootroot-X99-Turbo:~/3TB$ cat Android11.0.tar.bz2.a* > Android11.0.tar.bz2 rootroot@rootroot-X99-Turbo:~/3TB$