7038 -- 【11.18测试】t4

7038 – t4

这不是跳舞增强版吗

考虑把原来两种做法优化

分治

单组询问分治，对于每一层处理经过当前层mid的区间贡献
预处理[l,mid]的后缀min和max，枚举右端点，对于[mid+1,r]的min和max是确定的，分类讨论拼起来的区间的min和max在哪一边

发现对于min和max都各有一个分界点k
$\forall i\in [k,mid]，min[i,r]=min[mid+1,r]$
$\forall i\in [l,k-1],min[i,r]=min[i,mid]$
然后发现二者的分界点把[l,mid]分成了三部分

对于第一部分，$ans=\sum min\cdot max$
对于第二部分，$ans=minR\cdot \sum max或maxR\cdot min$
对于第三部分，$ans=minR\cdot minL\cdot len$
所以分别预处理四者的后缀和即可

考虑扩展到多组询问，先离线询问，然后还是分治做法，先处理经过当前中点的区间的贡献，再递归下去解决（相当于把一个询问区间拆成log段）

对于一个区间[x,y]，在处理[l,r]时已经处理了经过mid的贡献，所以只需要再分别考虑[x,mid]和[mid+1,y]的贡献即可

对于区间[l,r]，还是预处理4个后缀和，枚举右端点然后用线段树去维护总和。先对节点预处理区间和num，每次分成3段区间打add标记，表示sum(贡献)+=add*num，然后维护区间和。询问按右端点排序，枚举到当前右端点时更新ans=$\sum$t[0/1/2/3].query(l,mid)

线段树

还是先离线询问，枚举右端点，考虑暴力就是用两个数组mn,mx去表示[l,r]的min和max，每次r++时更新数组

考虑用线段树去优化这个过程，用单调栈（存下标）去维护，每次先弹栈，再把[q[top]+1,r]这段区间的mn数组改成a[i]，每个a[i]只会进一次出一次，维护区间min/max覆盖标记和区间答案

然后如果把不同的r对应的mn数组看成是mn数组的不同版本（r=1就是版本1，r=2就是版本2）
那么询问L,R，其实就是对[L,R]的每个版本询问[L,R]的和

然后就变成了维护历史和的一个操作
并没有想到覆盖标记怎么搞，先把覆盖标记转化成加标记，每次弹栈的时候把对应区间减去a[q[top]]，最后再把[q[top]+1,r]加上a[i]

然后考虑维护几个标记，首先是mn和mx的加标记
$mx=mx+a,mn=mn+b$
$\sum mx=\sum mx+a\cdot sz$
$\sum mn=\sum mn+b\cdot sz$
$\sum mx\cdot mn=\sum (mx+a)(mn+b)=\sum mx\cdot mn+a\sum mn+b\sum mx+ab\cdot sz$

然后是更新s(历史和)的标记
$s=s+c\sum mx\cdot mn$

问题是在合并标记的时，会发现标记不够用

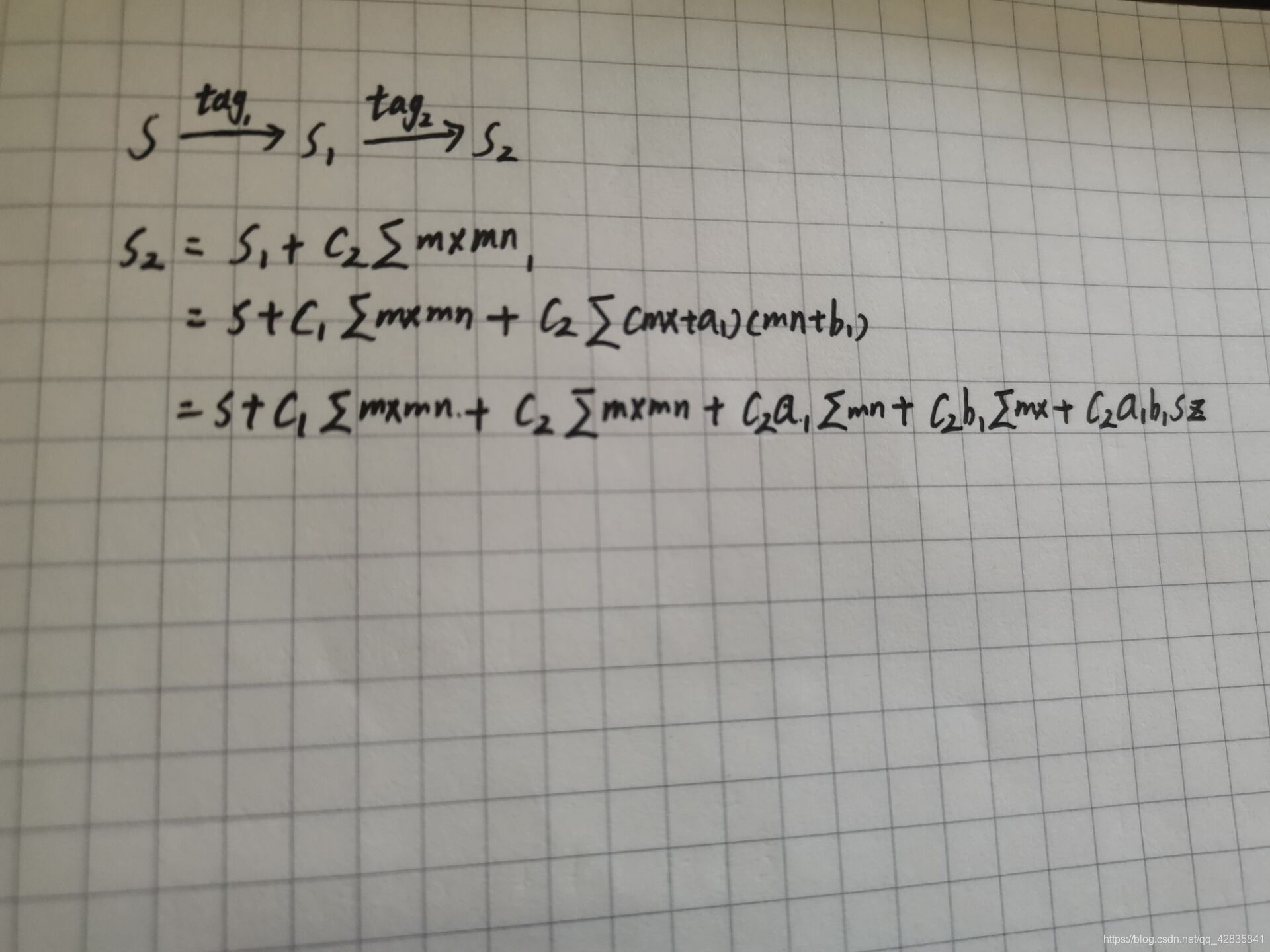
后面那一堆东西没办法只用一个c表示出来

所以维护c,d,e,f表示$s=s+c\sum mxmn+d\sum mn+e\sum mx+f\cdot sz$
然后是标记合并：

对mx加就打(k,0,0,0,0,0)的标记
对mn加就打(0,k,0,0,0,0)的标记
每次更新完打(0,0,1,0,0,0)的标记表示更新历史和