mmse专题
MMSE估计(二):从估计到估计器
【本文内容摘自"Signals, Systems and Inferences"之"8.2-From Estimate to an Estimator", by Alan V.Oppenheim and George C.Verghese, 2010.】 上面我们得到对于特定的 X = x X=x X=x,有 y ^ ( x ) = E [ Y ∣ X = x ] . \hat y(x)={
MMSE估计(一):连续随机变量的估计
【本文内容摘自"Signals, Systems and Inferences"之"8.1-Estimation of a Continuous Random Variable", by Alan V.Oppenheim and George C.Verghese, 2010.】 连续随机变量的MMSE估计 首先,我们假定对随机变量 Y Y Y感兴趣想要估计它的值,但我们只知道它的概率密度函
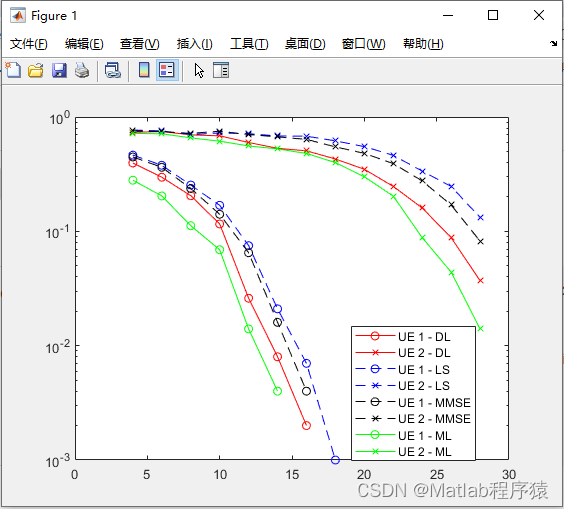
【MATLAB源码-第140期】基于matlab的深度学习的两用户NOMA-OFDM系统信道估计仿真,对比LS,MMSE,ML。
操作环境: MATLAB 2022a 1、算法描述 深度学习技术在无线通信领域的应用越来越广泛,特别是在非正交多址接入(NOMA)和正交频分复用(OFDM)系统中,深度学习技术被用来提高信道估计的性能和效率。信道估计是无线通信系统中的关键技术之一,它直接影响着系统的通信质量和可靠性。本文将详细介绍深度学习在2用户NOMA-OFDM系统信道估计中的应用,并与传统的最小二乘(LS)、最小均方误差
如何推导MMSE检测公式?
【转】如何推导MMSE检测公式? 这两天用到MMSE检测,对于它的推导,我前期只是在“知其然”,今天就来“知其所以然”,来证明一下MMSE检测公式。 MMSE检测用来求解什么? 首先,要知道信道的基本模型: y = Hx + n \textbf{y}=\textbf{H}\textbf{x}+\textbf{n} y=Hx+n H \textbf{H} H是信道矩阵, x \textbf
MMSE滤波/均衡矩阵:两个视角,推导与MATLAB实现
问题背景 考虑MIMO上行通信场景,基站配有 N N N根天线, K K K个单天线用户同时向基站发送数据符号符号。信道矩阵为 H ∈ C N × K \mathbf{H}\in \mathcal{C}^{N\times K} H∈CN×K,符号向量为 s = ( s 1 , . . . , s K ) T \mathbf{s}=(s_1,...,s_K)^T s=(s1,...,sK)T,
MMSE 预编码公式推导
考虑一个多用户多输入单输出MU-MISO下行通信场景,基站端配置有 N N N根天线,其服务该小区下 K K K个单天线用户。假定信道为平坦瑞利衰落信道,记为 H ∈ C N × K \mathbf{H}\in\mathcal{C}^{N\times K} H∈CN×K,基站最大发射功率为 P P P。则最小均方误差准则下的预编码矩阵为下面优化问题的最优解 min W E n , s [ ∣
【转】LS和MMSE的区别
ls 是误差平方和最小,mmse是误差平方和均值最小。它们的准则是不同的,一个是确定意义的,一个是统计意义。虽然统计意义的量实际也要用样本来计算,但是也不能说他们是等价的吧。MMSE要到相关矩阵(虽然也要用样本来计算),但是LS中却没有统计相关量的影子。 更具体的说,如果观测到的含噪结果Y是待估计参数X的一个函数:F(X)=Y。MMSE准则是基于最小化E{(X’-X)^H*(X’-X)}来计算估
Multi-Cell Downlink Beamforming: Direct FP, Closed-Form FP, Weighted MMSE
这里写自定义目录标题 Direct FPClosed-Form FPthe Lagrangian functionthe Lagrange dual function: maximizing the Lagrangianthe Lagrange dual problem: minimizing the Lagrange dual functionClosed-Form FP Weighted
简单的数字信号插值、抽取及成型,MMSE误差分析
#简单的数字信号插值、抽取及成型,MMSE误差分析 主题: 对于一个信号,奈奎斯特采样后的序列进行9倍插值,之后2倍抽取,选择不同的升余弦滚降因子插值滤波器,分析4.5倍插值后序列和实际采样后的对应序列误差情况。 此处的插值与抽取倍数均可调整,以实现不同分数倍的信号插值。使用升余弦滚降滤波器成型。 算法流程图如下: 需要注意虽然理论上奈奎斯特采样频率大于2倍频即可,但实际仿真为了追求效果,最